Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông hay và khó có đáp án

199 lượt xem

Bài trước

Bài sau

CHƯƠNG I: Hệ thức lượng trong tam giác vuông

MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO

A. Kiến thức cần nhớ

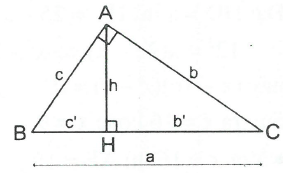
Tam giác ABC vuông tại A, đường cao AH (h.1.1). Khi đó ta có:

Ảnh đính kèm

1) $b^{2} = a b'; c^{2} = a c'$ ;

2) $h^{2} = b' c'$ ;

3) $b c = a h$ ;

4) $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ ;

5) $a^{2} = b^{2} + c^{2}$ (định lí Py-ta-go).

B. Một số ví dụ

Ví dụ 1. Cho tam giác ABC cân tại A ( $\hat{A} \neq 90 °$ ), đường cao BH. Chứng minh rằng: $\frac{1}{C H} = \frac{2 A B}{B C^{2}}$

Giải

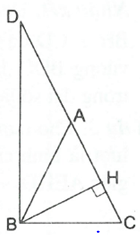
Ảnh đính kèm

Trên tia đối của tia AC lấy điểm D sao cho $A D = A C$ .

Do đó $B A = A C = A D = \frac{1}{2} C D$ .

Tam giác BCD có đường trung tuyến BA ứng với cạnh CD và $B A = \frac{1}{2} C D$ nên tam giác BCD vuông tại B.

Xét $Δ B C D$ vuông tại B, đường cao BH ta có: $B C^{2} = C D . C H$ (hệ thức 1).

Suy ra $B C^{2} = 2 A B . C H$ (vì $C D = 2 A B$ ). Do đó $\frac{1}{C H} = \frac{2 A B}{B C^{2}}$

Ví dụ 2. Hình thang ABCD có $\hat{A} = \hat{D} = 90 °$ và $B D ⊥ B C$ . Biết $A D = 12 c m, C D = 25 c m$ . Tính diện tích hình thang.

Giải

Vẽ $B H ⊥ C D$ .

Tứ giác ABHD có ba góc vuông nên là hình chữ nhật.

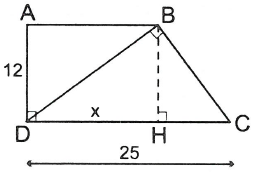
Ảnh đính kèm

Suy ra $B H = A D = 12 c m$ và $A B = D H$ .

Xét $Δ B D C$ vuông tại B, đường cao BH ta có:

$B H^{2} = H D . H C$ (hệ thức 2).

Đặt $H D = x$ thì $H C = 25 - x$ ta được:

$12^{2} = x (25 - x) \Leftrightarrow x^{2} - 25 x + 144 = 0$

hay $(x - 16) (x - 9) = 0$ .

Suy ra $x = 16$ hoặc $x = 9$ .

Với $x = 16$ thì $A B = 16$ .

Diện tích hình thang là: $S = \frac{(16 + 25) . 12}{2} = 246 (c m^{2})$ .

Với $x = 9$ thì AB=9.

Diện tích hình thang là: $S = \frac{(9 + 25) . 12}{2} = 204 (c m^{2})$ .

Ví dụ 3. Cho tam giác ABC vuông tại A, đường cao AH, BC = 2a. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Tính giá trị lớn nhất của diện tích tứ giác AEHD.

Giải

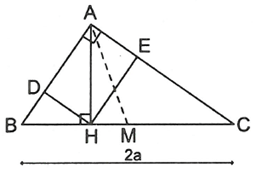
Ảnh đính kèm

Vẽ đường trung tuyến AM thì $A M = \frac{1}{2} B C = a$ .

Tứ giác AEHD có ba góc vuông nên là hình chữ nhật. Diện tích hình chữ nhật này là: $S = A D . A E$ .

Xét $Δ A B H$ vuông tại H ta có: $A H^{2} = A B . A D$ (hệ thức 1), suy ra $A D = \frac{A H^{2}}{A B}$

Tương tự ta có $A E = \frac{A H^{2}}{A C}$ . Do đó $S = \frac{A H^{2}}{A B} . \frac{A H^{2}}{A C} = \frac{A H^{4}}{A B . A C}$ .

Mặt khác $A B . A C = B C . A H$ (hệ thức 3) nên $S = \frac{A H^{4}}{B C . A H} = \frac{A H^{3}}{B C}$ .

Suy ra $S \leq \frac{A M^{3}}{B C}$ (vì $A H \leq A M$ )

Do đó $S \leq \frac{a^{3}}{2 a} = \frac{a^{2}}{2}$ (dấu "=" xảy ra $\Leftrightarrow Δ A B C$ vuông cân tại A).

Vậy $\max S = \frac{a^{2}}{2}$ khi $Δ A B C$ vuông cân tại A.

Ví dụ 4. Cho ba điểm A, B, C, trong đó A, B cố định, $A B = B C = a$ . Vẽ tam giác ADE vuông tại A sao cho AC là đường cao. Tìm giá trị nhỏ nhất của tổng $\frac{1}{A D^{2}} + \frac{1}{A E^{2}}$ .

Giải

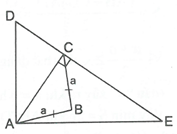
Ảnh đính kèm

Ta có AC là đường cao của tam giác ADE vuông tại A nên

$\frac{1}{A D^{2}} + \frac{1}{A E^{2}} = \frac{1}{A C^{2}}$ (hệ thức 4)

Tổng $\frac{1}{A D^{2}} + \frac{1}{A E^{2}}$ có giá trị nhỏ nhất có giá trị nhỏ nhất $\Leftrightarrow \frac{1}{A C^{2}}$ có giá trị lớn nhất.

Xét ba điểm $A, B, C$ ta có $A C \leq A B + B C = 2 a$ (dấu “=” xảy ra khi B là trung điểm của AC).

Vậy $\min (\frac{1}{A D^{2}} + \frac{1}{A E^{2}}) = \frac{1}{{(2 a)}^{2}} = \frac{1}{4 a^{2}}$ khi B là trung điểm AC.

Ví dụ 5. Cho hình thang ABCD, $\hat{A} = \hat{D} = 90 °$ , hai đường chéo vuông góc với nhau. Cho biết $A B = a, C D = b$ .

a) Tìm giá trị nhỏ nhất của diện tích hình thang ABCD.

b) Chứng minh rằng các độ dài AC, BD và $A B + C D$ có thể là độ dài ba cạnh của một tam giác vuông.

Giải

a) $Δ A D B$ và $Δ D C A$ có: $\hat{A} = \hat{D} = 90 °$ ; $\hat{A D B} = \hat{D C A}$ (cùng phụ với góc BDC).

Do đó $Δ A D B ~ Δ D C A$ (g.g).

Suy ra $\frac{A B}{D A} = \frac{A D}{D C} \Rightarrow A D^{2} = A B . C D = a . b$

Do đó $A D = \sqrt{a b}$ .

Diện tích hình thang ABCD là:

$S = \frac{(A B + C D) A D}{2} = \frac{(a + b) \sqrt{a b}}{2}$

Vì $\frac{a + b}{2} \geq \sqrt{a b}$ (bất đẳng thức Cô-si) nên $S \geq \sqrt{a b} . \sqrt{a b} = a b$

(dấu “=” xảy ra khi a = b hay khi ABCD là hình vuông).

Vậy $\min S = a b$ khi ABCD là hình vuông.

b) Xét $Δ A D B$ vuông tại A ta có:

$B D^{2} = A B^{2} + A D^{2}$ $= a^{2} + a b$ $= a (a + b)$

Xét tổng $A C^{2} + B D^{2}$ $= b (a + b) + a (a + b)$ $= {(a + b)}^{2}$ mà ${(A B + C D)}^{2} = {(a + b)}^{2}$ . Vậy $A C^{2} + B D^{2} = {(A B + C D)}^{2}$ .

Do đó theo định lí Py-ta-go đảo thì AC, BD và $A B + C D$ có thể là độ dài ba cạnh của một tam giác vuông.

C. Bài tập vận dụng

Vận dụng hệ thức (1)

1.1. Cho tam giác ABC vuông tại A, $A B = c, A C = b$ . Vẽ đường cao AH. Gọi E và F lần lượt là hình chiếu của H trên AB và AC. Tính theo b và c giá trị của các tỉ số:

a) $\frac{H B}{H C}$ ;

b) $\frac{B E}{C F}$ .

1.2. Cho tam giác ABC vuông tại A, $B C = 20 c m$ . Biết tỉ số hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là $9 : 16$ . Tính diện tích tam giác ABC.

1.3. Cho tam giác ABC cân tại A. Các tia phân giác của góc A và góc B cắt nhau tại O. Biết $O A = 2 \sqrt{3} c m$ , $O B = 2 c m$ , tính độ dài AB.

1.4. Cho tam giác ABC cân tại A, góc A nhọn, trực tâm H. Biết $H A = 7 c m$ , $H B = H C = 15 c m$ . Tính diện tích tam giác ABC.

Vận dụng hệ thức (2)

1.5. Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích các tam giác ABH và ACH lần lượt là $54 c m^{2}$ và $96 c m^{2}$ . Tính độ dài BC.

1.6. Cho hình thang cân ABCD, $A B / / C D$ , $A D ⊥ A C$ . Biết $A B = 7 c m, C D = 25 c m$ . Tính diện tích hình thang.

1.7. Cho hình thang ABCD, $\hat{A} = \hat{D} = 90 °$ . Hai đường chéo vuông góc với nhau tại O. Biết $O B = 5, 4 c m$ ; $O D = 15 c m$ .

a) Tính diện tích hình thang;

b) Qua O vẽ một đường thẳng song song với hai đáy, cắt AD và BC lần lượt tại M và N. Tính độ dài MN.

1.8. Cho trước các đoạn thẳng a và b ( $a \geq b$ ). Hãy dựng một đoạn thẳng thứ ba x sao cho x là trung bình nhân của hai đoạn thẳng a và b.

Vận dụng hệ thức (4)

1.9. Cho hình vuông ABCD cạnh 1. Gọi M là một điểm nằm giữa B và c. Tia AM cắt đường thẳng CD tại N. Tính giá trị của biểu thức $P = \frac{1}{A M^{2}} + \frac{1}{A N^{2}}$ .

1.10. Cho hình thoi ABCD, $A B = 2 c m$ , $\hat{A} = 120 °$ . Trên cạnh BC lấy điểm E sao cho $\hat{B A E} = 15 °$ . Tia AE cắt đường thẳng CD tại F. Chứng minh rằng $\frac{1}{A E^{2}} + \frac{1}{A F^{2}} = \frac{1}{3}$ .

1.11. Cho hình thang ABCD, $\hat{A} = \hat{D} = 90 °$ , $A D = C D$ và hai đáy không bằng nhau. Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng $\frac{1}{A D^{2}} = \frac{1}{C B^{2}} + \frac{1}{C E^{2}}$ .

1.12. Cho hình thoi ABCD, đường cao AH. Cho biết $A C = m$ ; $B D = n$ và $A H = h$ .

Chứng minh rằng $\frac{1}{h^{2}} = \frac{1}{m^{2}} + \frac{1}{n^{2}}$ .

1.13. Cho tam giác ABC vuông tại A, $A B = 15 c m, A C = 20 c m$ . Vẽ hình chữ nhật DEFG nội tiếp tam giác ABC sao cho D thuộc cạnh AB; E thuộc cạnh AC; F và G thuộc cạnh BC. Xác định vị trí của D và E để diện tích hình chữ nhật DEFG là lớn nhất. Tính diện tích lớn nhất đó.

Vận dụng hệ thức (5) Định lí Py-ta-go

1.14. Cho tam giác ABC, đường trung tuyến AM.

Chứng minh rằng $A B^{2} + A C^{2} = 2 A M + \frac{B C^{2}}{2}$ .

Áp dụng: Tam giác ABC có $A B = 5, A C = 7$ và $B C = 10$ . Tính độ dài đường trung tuyến AM.

1.15. Cho tam giác ABC, $\hat{A} = 60 °$ . Đặt $B C = a, C A = b, A B = c$ .

Chứng minh rằng $a^{3} < b^{3} + c^{3}$ .

1.16. Cho tam giác ABC, điểm M nằm giữa B và C. Chứng minh rằng:

$A B^{2} . M C + A C^{2} . M B - A M^{2} . B C = M B . M C . B C$

1.17. Cho tam giác ABC. Đặt $B C = a, C A = b, A B = c$ . Chứng minh rằng:

a) Nếu $\hat{A} < 90 °$ thì $a^{2} < b^{2} + c^{2}$ ;

b) Nếu $\hat{A} > 90 °$ thì $a^{2} > b^{2} + c^{2}$ ;

c) Nếu $\hat{A} = 90 °$ thì $a^{2} = b^{2} + c^{2}$ .

1.18. Cho tam giác ABC. Đặt $B C = a, C A = b, A B = c$ . Chứng minh rằng:

a) Nếu $a^{2} < b^{2} + c^{2}$ thì $\hat{A} < 90 °$ ;

b) Nếu $a^{2} > b^{2} + c^{2}$ thì $\hat{A} > 90 °$ ;

c) Nếu $a^{2} = b^{2} + c^{2}$ thì $\hat{A} = 90 °$ .

1.19. Cho tam giác ABC, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Độ dài các đường cao tương ứng là $h_{a}, h_{b}, h_{c}$ . Chứng minh rằng nếu $\frac{1}{h_{a}^{2}} = \frac{1}{h_{b}^{2}} + \frac{1}{h_{c}^{2}}$ thì $h_{b} = c$ và $h_{c} = b$ .

1.20. Cho hình thang ABCD, $\hat{A} = \hat{D} = 90 °$ , hai đường chéo vuông góc với nhau tại O. Cho biết $A D = 12 c m$ ; $C D = 16 c m$ . Tính các độ dài OA, OB, OC, OD.

1.21. Cho tam giác ABC vuông tại A, đường cao $A H = h, B C = a$ . Vẽ $H D ⊥ A B$ , $H E ⊥ A C$ . Ta đặt $B D = m, C E = n$ . Chứng minh rằng:

a) $h^{3} = a . m . n$ ;

b) $\sqrt[3]{a^{2}} = \sqrt[3]{m^{2}} + \sqrt[3]{n^{2}}$

1.22. Cho tam giác nhọn ABC. Ba đường cao AD, BE, CF cắt nhau tại H. Trên các đoạn thẳng HA, HB, HC lần lượt lấy các điểm M, N, P sao cho $\hat{B M C} = \hat{C N A} = \hat{A P B} = 90 °$ . Chứng minh rằng:

a) Các tam giác ANP, BMP và CMN là những tam giác cân;

b) Diện tích tam giác MBC là trung bình nhân của diện tích các tam giác ABC và HBC.

1.23. Cho năm đoạn thẳng a, b, c, d, e trong đó bất cứ ba đoạn thẳng nào cũng lập thành một tam giác. Chứng minh rằng tồn tại ba đoạn thẳng lập thành một tam giác có ba góc nhọn.

1.24. Cho tứ giác ABCD, AC = 6, BD = 4. Chứng minh rằng:

a) Tồn tại hai cạnh của tứ giác nhỏ hơn 5;

b) Tồn tại một cạnh của tứ giác lớn hơn 3,6.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông hay và khó có đáp án

Xem thêm các chương trình khác: