Chứng minh 2 đường thẳng song song trong đường tròn có đáp án

459 lượt xem

Bài trước

Bài sau

CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG

A. Phương pháp giải

Để chứng minh hai đường thẳng song song, ta có các cách sau:

- Chứng minh các cặp góc so le trong, đồng vị bằng nhau; cặp góc trong cùng phía bù nhau

- Chứng minh hai đường thẳng cùng vuông góc, cùng song song với đường thẳng thứ 3

- Sử dụng các định lý Thales đảo, định lý đường trung bình để chứng minh song song.

B. Ví dụ minh họa

Ví dụ 1. Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).

Hướng dẫn giải

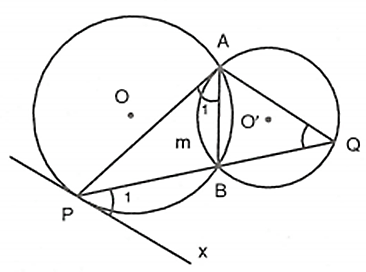
Ảnh đính kèm

Ta có $\hat{P_{1}} = \hat{A_{1}}$ (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung $\overset{⏜}{B P}$ ). $\hat{Q} = \hat{A_{1}}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $\overset{⏜}{A m B}$ ).

Suy ra $\hat{P_{1}} = \hat{Q}$ .

Do đó $P x$ // AQ (vì có cặp góc so le trong bằng nhau).

Ví dụ 2. Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Gọi P là điểm thuộc (O). Các đường thẳng PA, PB lần lượt cắt (O') tại A', B'. Chứng minh đường thẳng A'B' song song với tiếp tuyến tại P của đường tròn (O).

Hướng dẫn giải

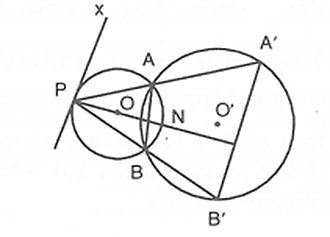
Ảnh đính kèm

Kéo dài PO cắt đường tròn (O) tại N. Ta có $\hat{P A B} = \hat{B'}$ (cùng bù với $\hat{B A A'}$ )

Mặt khác $\hat{P A B} = \hat{P N B}$ .

Do PN là đường kính nên $\hat{P N B} + \hat{B P N} = 90 °$

Từ đây $\hat{B'} + \hat{B P N} = 90 °$ .

Hay $P O ⊥ A' B'$ (3)

Từ $P x$ là tiếp tuyến với (O), ta có $O P ⊥ P x$ (4)

Từ (3) và (4) ta có $P x$ // A'B'.

Ví dụ 3. Cho đường tròn (O) tiếp xúc trong với đường tròn (O') ở P. Qua P vẽ hai cát tuyến PAA' và PBB' ( $A, B \in (O)$ và $A', B' \in (O')$ ). Chứng minh AB // A'B'.

Hướng dẫn giải

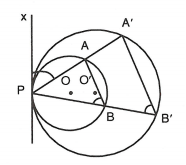
Ảnh đính kèm

Do vai trò của hai cát tuyến PAA' và PBB' là như nhau nên không mất tính tổng quát ta có thể giả sử tia PA nằm giữa hai tia $P x$ ( $P x$ là tiếp tuyến tại P của hai đường tròn) và PB (hình vẽ).

Trong đường tròn (O), ta có

$s d \overset{⏜}{A P x} = \frac{1}{2} s d \overset{⏜}{P A}$

(góc tạo bởi tiếp tuyến Px và dây PA ).

$s d \overset{⏜}{P B A} = \frac{1}{2} \overset{⏜}{P A}$

(góc nội tiếp chắn cung $\overset{⏜}{P A}$ ).

Suy ra $s d \overset{⏜}{A P x} = s d \overset{⏜}{P B A}$ , hay $\hat{A P x} = \hat{P B A}$ (5)

Chứng minh tương tự, trong đường tròn (O'), ta có $\hat{A P x} = \hat{A' B' P}$ (6)

Từ (5) và (6) suy ra $\hat{A B P} = \hat{A' B' P}$ , do đó AB // A'B' (hai góc ở vị trí đồng vị bằng nhau).

C. Bài tập tự luyện

Bài 1. Cho hai đường tròn (O) và $(O')$ tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyến của đường tròn (O) tại điểm B cắt đường tròn $(O')$ tại C và D (C nằm giữa B và D). Các tia CA, DA cắt đường tròn (O) theo thứ tự tại E và F.

a) Chứng minh rằng $E F / / C D .$

b) Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Tính số đo góc $\hat{B A M} .$

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Chứng minh 2 đường thẳng song song trong đường tròn có đáp án

Xem thêm các chương trình khác: