Bài toán quỹ tích cực hay có đáp án

175 lượt xem

BÀI TOÁN QUỸ TÍCH

A. Phương pháp giải

1. Các quỹ tích cơ bản

Để tìm quỹ tích trong mặt phẳng, người ta thường dựa vào các quỹ tích cơ bản. Một số quỹ tích sau đây thường được mọi người thừa nhận là quỹ tích cơ bản:

Quỹ tích 1: Quỹ tích những điểm cách đều hai điểm A và B cố định là đường trung trực của đoạn thẳng AB.

Quỹ tích 2: Quỹ tích những điểm cách đều hai cạnh của một góc là đường phân giác của góc đó.

Quỹ tích 3: Quỹ tích những điểm cách đều đường thẳng xy cố định một khoảng a cho trước là hai đường thẳng song song với xy và cách xy một khoảng a cho trước.

Quỹ tích 4: Quỹ tích những điểm cách đều điểm O cố định một khoảng R cho trước là đường tròn có tâm là O và bán kính bằng R.

Quỹ tích 5: Quỹ tích những điểm nhìn đoạn thẳng AB cố định dưới một góc $α$ không đổi ( $0 ° < α < 180 °$ ) là hai cung chứa góc $α$ dựng trên đoạn thẳng AB.

Đặc biệt, nếu $α = 90 °$ thì ta nhận được.

Quỹ tích 5a: Quỹ tích những điểm nhìn đoạn thẳng AB cố định dưới một góc vuông là đường tròn đường kính AB.

2. Các bước giải một bài toán quỹ tích

- Muốn chứng minh quỹ tích (tập hợp) các điểm M thỏa mãn tính chất $τ$ là một hình H nào đó, ta phải chứng minh hai phần:

- Phần thuận: Mọi điểm có tính chất $τ$ đều thuộc hình H.

- Giới hạn. Xem điểm M chỉ thuộc một phần $H_{1}$ của hình H hay cả hình H.

- Phần đảo: Mọi điểm thuộc hình H hoặc thuộc phần $H_{1}$ (nếu có giới hạn) đều có tính chất $τ$ .

Kết luận: Quỹ tích (tập hợp) các điểm M có tính chất $τ$ là hình H (hoặc thuộc phần $H_{1}$ ).

B. Ví dụ minh họa

Ví dụ 1. Cho nửa đường tròn đường kính BC. Một điểm A di động sao cho tam giác ABC có ba góc nhọn và trọng tâm G của tam giác nằm trên nửa đường tròn đó. Tìm quỹ tích điểm A.

Hướng dẫn giải

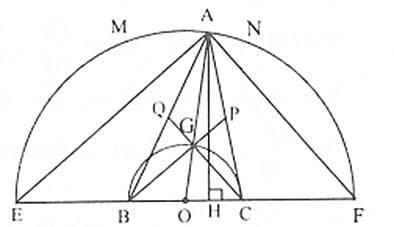
Ảnh đính kèm

Phần thuận.

Cách 1. Trên đường thẳng BC lấy hai điểm E, F sao cho B là trung điểm CE, C là trung điểm BF.

Ta có: $E F = 3 B C$ cố định (1)

Gọi P và Q lần lượt là giao điểm của BG và AC; CG và AB

CQ là đường trung bình của $Δ A B F$ nên $C Q / / A F$ .

BP là đường trung bình của $Δ A C E$ nên $B P / / A E$

Mà $C Q ⊥ B P$ nên $A F ⊥ A E$ $\Rightarrow \hat{E A F} = 90 °$ (2)

Từ (1) và (2), suy ra A di động trên đường tròn đường kính EF.

Phần đảo.

Lấy điểm A biết bất kì thuộc cung nhỏ MN, gọi G là giao điểm của OA với nửa đường tròn đường kính BC $\Rightarrow A O$ là đường trung tuyến của $Δ A B C$ .

Ta có: $O G = \frac{1}{2} B G$ $= \frac{1}{3} O A \Rightarrow G$ là trọng tâm $Δ A B C$ .

Kết luận. Vậy tập hợp điểm A là cung nhỏ MN (trừ hai điểm M, N).

Ví dụ 2. Cho ba điểm A, B, C cố định nằm trên đường thẳng d (B nằm giữa A và C). Một đường tròn $(O)$ thay đổi luôn đi qua A và B, gọi DE là đường kính của đường tròn $(O)$ vuông góc với d. CD và CE cắt đường tròn $(O)$ lần lượt tại M và N. Khi đường tròn $(O)$ thay đổi thì hai điểm M và N di động trên đường cố định nào?

Hướng dẫn giải.

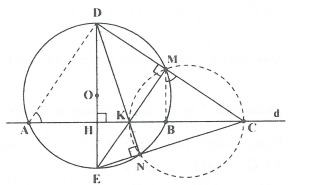
Ảnh đính kèm

Gọi H, K lần lượt là giao điểm của CA với DE và EM. Do A, B, C cố định nên H cố định.

- $Δ C M K$ và $Δ C H D$ có: $\hat{M} = \hat{H} = 90 °$

$\hat{D C H}$ là góc chung.

Vậy: $Δ C M K ~ Δ C H D$ (g.g)

$\Rightarrow \frac{C K}{C D} = \frac{C M}{C H}$

$\Rightarrow C K . C H = C M . C D$ (1)

- $Δ C M B$ và $Δ C A D$ có: $\hat{C M B} = \hat{C A D}$ (do tứ giác ABMD nội tiếp); $\hat{A C D}$ là góc chung.

Vậy: $Δ C M B ~ Δ C A D$ (g.g)

$\Rightarrow \frac{C M}{C A} = \frac{C B}{C D}$ $\Rightarrow C M . C D = C A . C B$ (2)

Từ (1) và (2) $\Rightarrow C K . C H = C A . C B$ $\Rightarrow C K = \frac{C A . C B}{C H}$ (không đổi)

$\Rightarrow K$ là điểm cố định.

- Tam giác CDE có K là trực tâm nên DN cũng đi qua điểm K cố định.

Mà $\hat{D M E} = \hat{D N E} = 90 °$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \hat{K M C} = \hat{K N C} = 90 °$ .

Vậy: Khi đường tròn $(O)$ thay đổi thì hai điểm M và N di động trên đường tròn cố định đường kính CK, với $C K = \frac{C A . C B}{C H}$ .

Ví dụ 3. Cho đường tròn ( $O; R$ ) và điểm P cố định nằm trong đường tròn). Dây cung AB thay đổi luôn đi qua P. Tiếp tuyến tại A và B với đường tròn cắt nhau tại M. Tìm quỹ tích điểm M.

Hướng dẫn giải.

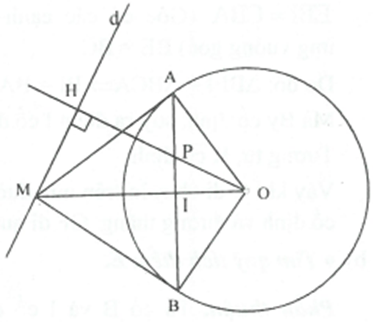
Ảnh đính kèm

Phần thuận. Gọi H là hình chiếu của M trên đường thẳng OP.

Gọi I là giao điểm của AB và MO.

Suy ra $A B ⊥ M O$ từ đó ta có $Δ O H M ~ Δ O I P$ (g.g)

$\Rightarrow \frac{O M}{O P} = \frac{O H}{O I}$ $\Rightarrow O M . O I = O H . O P$ (1)

Mặt khác $Δ O A M$ vuông tại A có:

$A I ⊥ M O$ nên $O A^{2} = O M . O I$ (2)

Từ (1) và (2) suy ra $O H . O P = O A^{2}$

$\Rightarrow O H = \frac{R^{2}}{O P}$ không đổi

$\Rightarrow M$ thuộc đường thẳng d vuông góc với OP tại điểm H và cách O một khoảng cách $O H = \frac{R^{2}}{O P}$ .

Phần đảo. Trên đường thẳng d lấy điểm $M'$ bất kì. Từ $M'$ kẻ tiếp tuyến $M' A', M' B'$ . Đường thẳng $A' B'$ cắt $M' O$ tại $I'$ .

Giả sử OH cắt $A' B'$ tại $P'$

Ta có

$O P' . O H = O I' . O M' = R^{2}$

$\Rightarrow O P' = \frac{R^{2}}{O H}$ $\Rightarrow P' \equiv P$ .

Kết luận. Quỹ tích của điểm M là đường thẳng d vuông góc với OP tại điểm H thỏa mãn $O H = \frac{R^{2}}{O P}$ .

C. Bài tập tự luyện

Bài 1. Cho đường tròn tâm O đường kính AB cố định, BC là dây cung bất kì. Trên tia đối của tia CB lấy điểm D sao cho $C D = B C$ . Gọi P là giao điểm của AC và DO. Tìm quỹ tích điểm P.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Các dạng bài tập Toán 9

Bài toán quỹ tích cực hay có đáp án

Xem thêm các chương trình khác: