Bài toán thực tế hình học có đáp án

211 lượt xem

Bài trước

Bài sau

CHUYÊN ĐỀ THỰC TẾ - BÀI TOÁN LIÊN QUAN ĐẾN HÌNH HỌC

A. Phương pháp giải

Áp dụng hợp lý các công thức hệ thức lượng trong tam giác vuông, định lý Py – ta – go, công thức tính diện tích chu vi các hình tam giác, chữ nhật, hình tròn, hình quạt tròn, … công thức tính diện tích xung quanh, diện tích toàn phần, thể tích hình nón, hình trụ, hình cầu.

B. Ví dụ minh họa

Ví dụ 1: Một máy bay đang bay trên độ cao 10km. Khi hạ cánh xuống mặt đất, đường bay của máy bay tạo một góc nghiêng so với mặt đất.

a) Nếu phi công muốn tạo góc nghiêng 50 thì cách sân bay bao nhiêu ki-lô-mét phải bắt đầu cho máy bay hạ cánh?

b) Nếu cách sân bay 350km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu?

Hướng dẫn giải:

a) Ta có hình vẽ như sau:

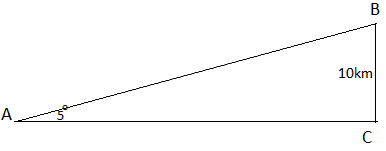
Ảnh đính kèm

Gọi các điểm như trên hình vẽ

Khi đó khoảng cách giữa máy bay và sân bay là AB

Xét tam giác vuông ABC có:

$sinA = \frac{BC}{AB}$ $\Rightarrow AB = \frac{B C}{\sin A} = \frac{10}{\sin 5^{\circ}} = 114, 7 k m$

b) Ta có hình vẽ như sau:

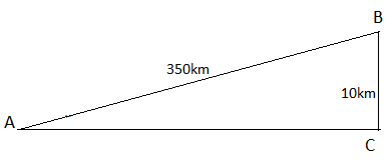
Ảnh đính kèm

Gọi các điểm như trên hình vẽ

Khi đó góc nghiêng tạo giữa máy bay và mặt đất là góc A

Xét tam giác vuông ABC, ta có:

$sinA = \frac{BC}{AC} = \frac{10}{350}$ $\Rightarrow A = 1^{0} 38^{'}$

Vậy góc nghiêng tạo giữa máy bay và mặt đất là 1^o38'.

Ví dụ 2: Một khối gỗ hình lập phương được sơn màu cả 6 mặt. Sau đó người ta cắt nó thành các khối lập phương đều nhau. Biết rằng tổng số mặt của các khối lập phương nhỏ được sơn bằng tổng số mặt các khối lập phương nhỏ chưa được được sơn. Hỏi có bao nhiêu khối lập phương nhỏ?

Hướng dẫn giải

Gọi x là số khối gỗ lập phương nhỏ đếm được trên 1 cạnh.

Vậy tổng số khối gỗ lập phương nhỏ $x^{3}$

Tổng số mặt gỗ lập phương nhỏ $6 . x^{3}$

Tổng số mặt của các khối lập phương nhỏ được sơn bằng tổng số mặt các khối lập phương nhỏ chưa được được sơn nên bằng $3 . x^{3}$

Tổng số mặt gỗ lập phương nhỏ được sơn $6 . x^{2}$

Vậy $3 x^{3} = 6 x^{2}$

$x = 2$

Số khối lập phương nhỏ $2.2.2 = 8$

Ví dụ 3: Một phễu đổ bê tông gồm một hình trụ phía trên gắn liền với một hình nón cụt, phía dưới có các kích thước như hình vẽ. Tính diện tích tôn thiết cần để gò nên phễu? (làm tròn đến mét vuông).

Ảnh đính kèm

Hướng dẫn giải

Diện tích xung quanh phần hình trụ trên là:

$S_{1} = π . d . h_{1} = 1, 2.0, 4 π$ $= 0, 48 π (m^{2})$

Độ sinh đường sinh hình nón cụt là:

$1 = \sqrt{1^{2} + 0, 5^{2}} = \frac{\sqrt{5}}{2} (m)$

Diện tích xung quanh phần nón cụt phía dưới là:

$S_{2} = π . (R + r) . l = (0, 6 + 0, 1) \frac{\sqrt{5}}{2} π$ $= 0, 35 π \sqrt{5} (m^{2})$ .

Diện tích xung quanh hay diện tích miếng tôn cần để đóng phễu đổ bê tông là:

$S = S_{1} + S_{2}$ $= 0, 48 π + 0, 35 π \sqrt{5} \approx 4 (m^{2})$ .

C. Bài tập tự luyện

Bài 1. Thang AB dài 7,6m tựa vào bức tường tạo thành góc 55^o so với phương nằm ngang. Hỏi chiều cao của bức tường (làm tròn đến chữ số thập phân thứ hai)?

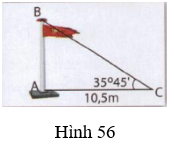
Bài 2. Tính chiều cao của cột cờ, biết bóng của cột cờ được chiếu bởi ánh sáng Mặt Trời xuống đất dài 10,5m và góc tạo bởi tia sáng với mặt đất là 35^o45’ (h.56).

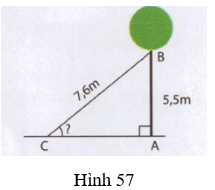
Ảnh đính kèm

Bài 3. Một con mèo ở trên cành cây cao 5,5m. Để bắt mèo xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó. Khi đó góc giữa thang với mặt đất là bao nhiêu, biết chiếc thang dài 7,6m (h.57)?

Ảnh đính kèm

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài toán thực tế hình học có đáp án

Xem thêm các chương trình khác: