CÁC BÀI TOÁN LIÊN QUAN ĐẾN TIẾP TUYẾN
A. Phương pháp giải
+) Sử dụng tính chất của hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến cùa một đường tròn cắt nhau tại một điểm thì:
Điếm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính (đi qua các tiếp điểm)
+) Sử dụng định nghĩa về tiếp tuyến, góc tạo bởi tia tiếp tuyến và dây cung và kiến thức hình học khác để giải quyết bài toán.
B. Ví dụ minh họa
Ví dụ 1: Cho đường tròn (O), điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm).
a) Chứng minh rằng OA ⊥ MN
b) Vẽ đường kính NOC. Chứng minh rằng MC//AO.
c) Tính độ dài các cạnh của tam giác AMN biết QM=3cm, OA=5cm.
Hướng dẫn giải
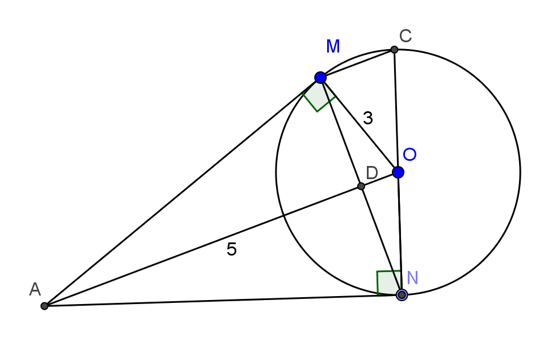
a) Ta có:
AM = AN ( theo tính chất của 2 tiếp tuyến cắt nhau)
Mà OM = ON ( vì cùng bằng R)
Suy ra AO là đường trung trực của MN.
Suy ra OA ⊥ MN
b) Xét tam giác MNC có: NC là đường kính nên suy ra ∠ NMC = 90o
NM ⊥ MC
Mà OA ⊥ MN (chứng minh trên)
MC//OA.
c) Xét tam giác vuông AMO. Theo định lý Py-ta-go ta có:
Vì AM = AN nên AN = 4cm.
Ta có: OA ⊥ MN (chứng minh trên)
Xét tam giác vuông AMO. Theo hệ thức lượng trong tam giác vuông ta có:
AO.MD = AM.MO
5.MD = 4.3
Suy ra MD = 12/5
Vì MN = 2 MD = 2.12/5 = 24/5(cm)
Vậy AM = AN = 4cm; MN = 24/5 cm.
Ví dụ 2: Cho đường tròn (O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua điểm I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD=4cm, tính chu vi tam giác MPQ.
Hướng dẫn giải
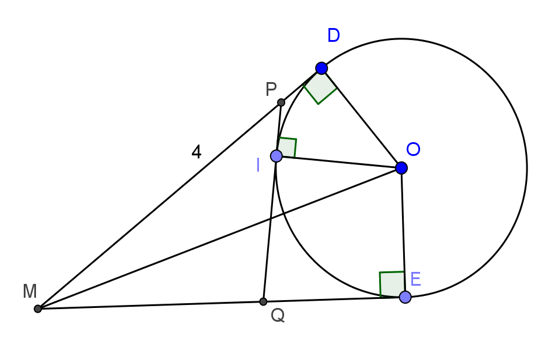
Ta có:
+ PD và PI là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại P
Suy ra PD = PI
+ QI và QE là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại Q
Suy ra QI = QE
+ MD và ME là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại M
Suy ra MD = ME
Chu vi tam giác MPQ là: MP + PQ + MQ
= MD- PD + PI + IQ + ME - QE
= MD - PI + PI + QE + MD - QE
= 2MD = 2.4 = 8(cm)
Vậy chu vi tam giác MPQ là 8cm.
Ví dụ 3: Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB đi qua tâm O của đường tròn đó.
a) Chứng minh rằng .
b) Khi cho tính bán kính đường tròn?
Hướng dẫn giải

a) Xét hai tam giác BMT và TMA có:
M chung
(cùng chắn cung nhỏ AT)
Suy ra tam giác BMT đồng dạng với tam giác TMA
Vậy .
b) Gọi bán kính đường tròn là R. Ta có
Thay số ta có
.
C. Bài tập tự luyện
Bài 1. Từ điểm A nằm bên ngoài đường tròn (O). Kẻ các tiếp tuyến AM, AN với đường tròn đó (M, N là các tiếp điểm).
a) Chứng minh rằng
b) Vẽ đường kính NOC, chứng minh rằng MC∥ AO.
c) Tính độ dài các cạnh của tam giác AMN biết
Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

