VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
I. LÝ THUYẾT
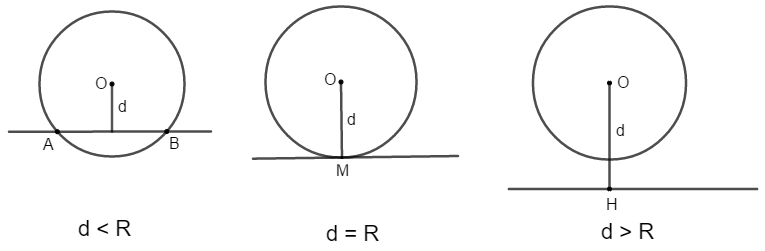
1. Gọi d là khoảng cách từ tâm O của đường tròn (O; R) đến đường thẳng thì:
cắt .
tiếp xúc với .
không cắt
2. Đường thẳng và đường tròn tiếp xúc nhau:
Định lí: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
II. BÀI TẬP VẬN DỤNG
Bài 1. Cho đường tròn (O; R), đường thẳng a cắt đường tròn tại hai điểm A và B. Gọi H là chân của đường vuông góc kẻ từ O đến đường thẳng a. Hãy so sánh OH với R.
Bài 2. Quan sát hình bên, hãy tìm số điểm chung giữa đường thẳng a và đường tròn (O; R) rồi so sánh OH với R (với C là tiếp điểm và H là chân đường vuông góc kẻ từ O đến đường thẳng a)
Bài 3. Gọi d là khoảng cách từ tâm đường tròn (O; R) đến đường thẳng a. Hãy điền vào bảng tóm tắt sau:
|
Vị ví tương đối giữa đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa d và R |
|
Đường thẳng và đường tròn cắt nhau |
|
|
|
Đường thẳng và đường tròn tiếp xúc nhau |
|
|
|
Đường thẳng và đường tròn không giao nhau |
|
|
Bài 4. Cho tam giác ABC vuông tại A có , . Từ C làm tâm vẽ các đường tròn , và . Hãy xét mối quan hệ của AB đối với mỗi đường tròn trên.
Bài 5. Điền vào các chỗ trống trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng).
|
R |
d |
Vị trí tương đối |
|
5cm |
3cm |
… |
|
6cm |
… |
Tiếp xúc nhau |
|
4cm |
7cm |
… |
Bài 6. Trên mặt phẳng tọa độ cho điểm A là (3, 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) với các trục tọa độ?
Bài 7. Cho điểm M cách đường thẳng xy một khoảng 8cm. Vẽ đường tròn (M; 10cm)
a) Chứng minh đường tròn (O) cắt đường thẳng xy
b) Gọi A và B là giao điểm của xy với (M). Tính AB
Bài 8. Cho , phân giác Az. Trên tia Az lấy điểm M sao cho AM = 8cm.
a) Vẽ đường tròn (M; 3cm), đường tròn này có cắt tia Ax hay Ay không? Vì sao?
b) Vẽ đường tròn (M; r), r bằng bao nhiêu để dường tròn này tiếp xúc với tia Ax? Đường tròn ấy có tiếp xúc với Ay không? Vì sao?
Bài 9. Cho đường tròn (O), điểm I nằm ngoài đường tròn. Vẽ đường tròn (I; IO) cắt đường tròn (O) tại A và B, cắt tia OI tại M. CMR hai tia MA, MB tiếp xúc với đường tròn (O).
Bài 10. Cho nửa đường tròn (O) đường kính AB = 2R. Hai điểm C, D di động trên nửa đường tròn sao cho CD = R. Gọi M, N là chân các đường vuông góc kẻ từ A, B đến đường thẳng CD. Tính diện tích lớn nhất của tứ giác AMNB.
Bài 11: Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ Ax và By vuông góc với AB. Trên Ax, By lần lượt lấy C và D sao cho . Kẻ .
a) Chứng minh H thuộc đường tròn tâm O đường kính AB
b) Xác định vị trí tương đối của đường thẳng CD với dường tròn (O).

