DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
I. LÝ THUYẾT
1. Tính chất của tiếp tuyến
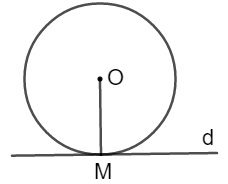
Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Để nhận biết một đường thẳng là tiếp tuyến của một đường tròn ta có hai dấu hiệu sau:
+ Dấu hiệu 1: Chứng minh khoảng cách từ tâm đến đường thẳng bằng R.
+ Dấu hiệu 2: Đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.
Ký hiệu:
tại H
là tiếp tuyến của
II. BÀI TẬP VẬN DỤNG
Bài 1. Cho đường tròn O ngoại tiếp tam giác đều ABC, AH là đường cao. Hãy vẽ tiếp tuyến của đường tròn tại A.
Bài 2. Cho điểm A nằm ngoài đường tròn . Hãy vẽ hai tiếp tuyến AB và AC.
Bài 3. Cho đường tròn (O) và một đường thẳng xy. Hãy dựng tiếp tuyến của đường tròn song song với xy.
Bài 4. Cho tam giác có . Vẽ đường tròn . Chứng minh rằng là tiếp tuyến của đường tròn.
Bài 5. Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn đi qua điểm B tiếp xúc với đường thẳng d tại A.
Bài 6. Cho đường tròn , dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C.
a) Chứng minh rằng CB là tiếp tuyến của đường tròn.
b) Cho biết bán kính của đường tròn bằng . Tính độ dài OC.
Bài 7 Cho đường tròn có bán kính , dây vuông góc với tại trung điểm của .
a) Tứ giác là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại , nó cắt đường thẳng tại . Tính độ dài theo .
Bài 8. Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ các tia tiếp tuyến Ax, By thuộc
cùng một nửa mặt phẳng bờ AB. Từ một điểm C trên nửa đường tròn vẽ một tiếp tuyến cắt
Ax, By lần lượt tại D và E.
a) Chứng minh rằng tích AD.BE không đổi;
b) Tính diện tích nhỏ nhất của tứ giác ABED.
Bài 9. Cho đường tròn tâm O và một dây . Gọi I là trung điểm của dây và trả cắt đường tròn tại điểm .
a) Chứng minh rằng tiếp tuyến với đường tròn tại điểm thì song song với dây .
b) Suy ra cách dựng các tiếp tuyến của đường tròn song song với một dây cho trước. Bài
toán này có bao nhiêu nghiệm?
Bài 10. Cho một hình thoi , các đường chéo và giao nhau tại điểm . Từ kẻ các đường thẳng theo thứ tự vuông góc với các cạnh
a) Chứng minh các điểm thẳng hàng và bốn điểm nằm trên một đường tròn.
b) Chứng minh đường tròn tâm , đi qua các điểm tiếp xúc với các cạnh của hình thoi.
c) Biết . Tính các cạnh của hình thoi và bán kính đường tròn đi qua bốn điểm .
Bài 11. Cho tam giác ABC cân tại A, BC = 2a. Vẽ đường tròn có tâm O trên BC và tiếp
xúc với hai cạnh bên. Một tiếp tuyến của đường tròn (O) cắt hai cạnh AB, AC lần lượt tại
M và N. Tính tích BM.CN.
Bài 12. Cho đường tròn (O; r) nội tiếp tam giác ABC, tiếp xúc với các cạnh BC, CA, AB
lần lượt tại D, E, F. Gọi p là nửa chu vi và S là diện tích của tam giác ABC. Chứng minh
rằng:
a)
b)
Bài 13. Cho tam giác ABC. BC = a; CA = b; AB = c. Vẽ đường tròn (K) bàng tiếp trong góc
A của tam giác ABC, tiếp xúc với các đường thẳng BC, CA, AB lần lượt tại D, E, F. Chứng
minh rằng:
a) (p là nửa chu vi của );
b) .
Bài 14. Cho nửa đường tròn (O; R) đường kính AB. Một đường thẳng xy tiếp xúc với đường tròn tại C. Gọi D và E lần lượt là hình chiếu của A và B trên xy. Chứng minh rằng:
a) C là trung điểm của DE;
b) Tổng AD + BE không đổi khi C di động trên nửa đường tròn;
c) Tích
Bài 15. Cho đường thẳng xy, một điểm A và đường tròn (O) nằm trên một nửa mặt phẳng bờ xy. Hãy dựng điểm sao cho nếu vẽ tiếp tuyến MB với đường tròn (O) thì .
Bài 16. Từ điểm M ở ngoài đường tròn (O; R) vẽ tiếp tuyến MA với đường tròn. Vẽ dây . Chứng minh rằng MB là tiếp tuyến của đường tròn.
Bài 17. Cho tam giác ABC, hai đường cao BD, CE cắt nhau tại H.
a) Chứng minh rằng bốn điểm A, D, H, E cùng nằm trên một đường tròn đường kính AH.
b) Gọi M là trung điểm của BC, chứng minh rằng MD là tiếp tuyến của đường tròn đường kính AH.
Bài 18. Một hình vuông cạnh 8 được chia thành 64 ô vuông nhỏ bằng nhau. Vẽ đường tròn (O; 4) với O là tâm hình vuông.
a) Chứng minh rằng đường tròn này tiếp xúc với bốn cạnh của hình vuông;
b) Có bao nhiêu ô vuông nhỏ nằm hoàn toàn trong đường tròn?

