Bài tập tính diện tích hình tròn và chu vi hình tròn cực hay, chi tiết

161 lượt xem

Bài trước

Bài sau

TÍNH DIỆN TÍCH, CHU VI HÌNH TRÒN, HÌNH QUẠT TRÒN, HÌNH VIÊN PHÂN

A. Phương pháp giải

Áp dụng các công thức sau để tính toán:

1. Hình tròn

Công thức tính diện tích hình tròn: $S = π R^{2}$ , trong đó R là bán kính của hình tròn.

Chu vi của hình tròn: $P = 2 π R$

2. Hình quạt tròn

Công thức tính diện tích hình quạt tròn bán kính R, cung $n °$ : $S = \frac{π . R^{2} . n}{360 °}$ hay $S = \frac{l R}{2}$ .

Chu vi hình quạt tròn bán kính R, cung $n °$ : $2 R + l$

Trong đó, R là bán kính hình tròn; n là số đo góc ở tâm, l là số đo cung bị chắn.

7. Hình viên phân, hình khác:

Đối với các hình khác, ta cắt ghép các hình đã cho đưa về hình quen thuộc, rồi sử dụng các công thức đã biết để tính toán.

B. Ví dụ minh họa

Ví dụ 1: Cho hình thang ABCD (AD//BC) có: $\hat{A} = \hat{D} = 60 °$ và AD = 4cm. Cạnh BC là đường kính của nửa đường tròn nội tiếp (như hình vẽ). Tính diện tích phần nằm trong hình thang và nằm ngoài nửa hình tròn.

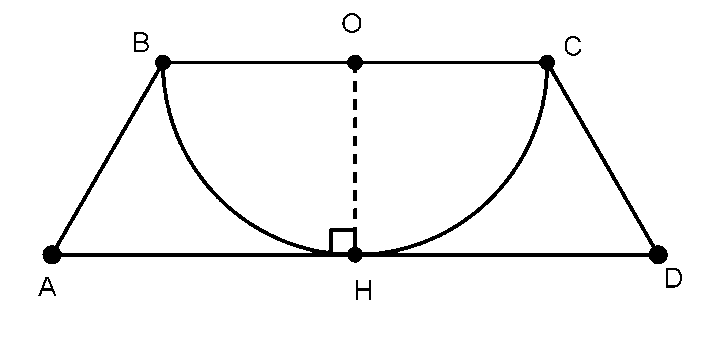
Ảnh đính kèm

Hướng dẫn giải

Từ B hạ BK $⊥$ AD, đặt AK = x

Xét $Δ A B K$ vuông tại K, ta có:

$\tan \hat{B A K} = \frac{B K}{A K}$ $\Leftrightarrow \tan 60 ° = \frac{B K}{x}$ $\Leftrightarrow B K = \sqrt{3} x$ $\Rightarrow O H = \sqrt{3} x$

Vì H thuộc nửa đường tròn đường kính BC

$\Rightarrow B C = 2 O H = 2 \sqrt{3} x$

Mà $A D = 2 A H + B C$ $= 2 x + 2 \sqrt{3} x$ $= (2 + 2 \sqrt{3}) x = 4$ $\Leftrightarrow x = \sqrt{3} - 1$

$\Rightarrow B C = 2 \sqrt{3} . (\sqrt{3} - 1)$ $= 6 - 2 \sqrt{3}, O H$ $= \sqrt{3} . (\sqrt{3} - 1)$ $= 3 - \sqrt{3}$

Diện tích hình thang ABCD là:

$S_{1} = \frac{(4 + 6 - 2 \sqrt{3}) (3 - \sqrt{3})}{2}$ $= 18 - 8 \sqrt{3} (c m^{2})$

Diện tích nửa hình tròn đường kính BC là:

$S_{2} = \frac{1}{2} π {(3 - \sqrt{3})}^{2}$ $= (6 - 3 \sqrt{3}) π (c m^{2})$

Diện tích hình cần tìm là:

$S_{1} - S_{2} = 18 - 8 \sqrt{3} - (6 - 3 \sqrt{3}) π (c m^{2})$ .

Ví dụ 2: Một đường hầm có mặt cắt vuông góc là một phần đường tròn như hình bên. Mặt cắt này có chiều cao lớn nhất là 5m, chiều rộng $10 \sqrt{3} m$ . Tính diện tích mặt cắt của đường hầm.

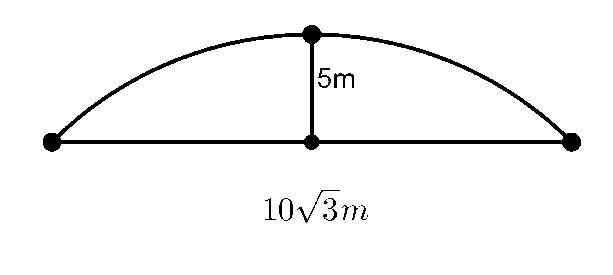
Ảnh đính kèm

Hướng dẫn giải

Vẽ đường tròn tâm O, bán kính R chứa phần đường tròn trên

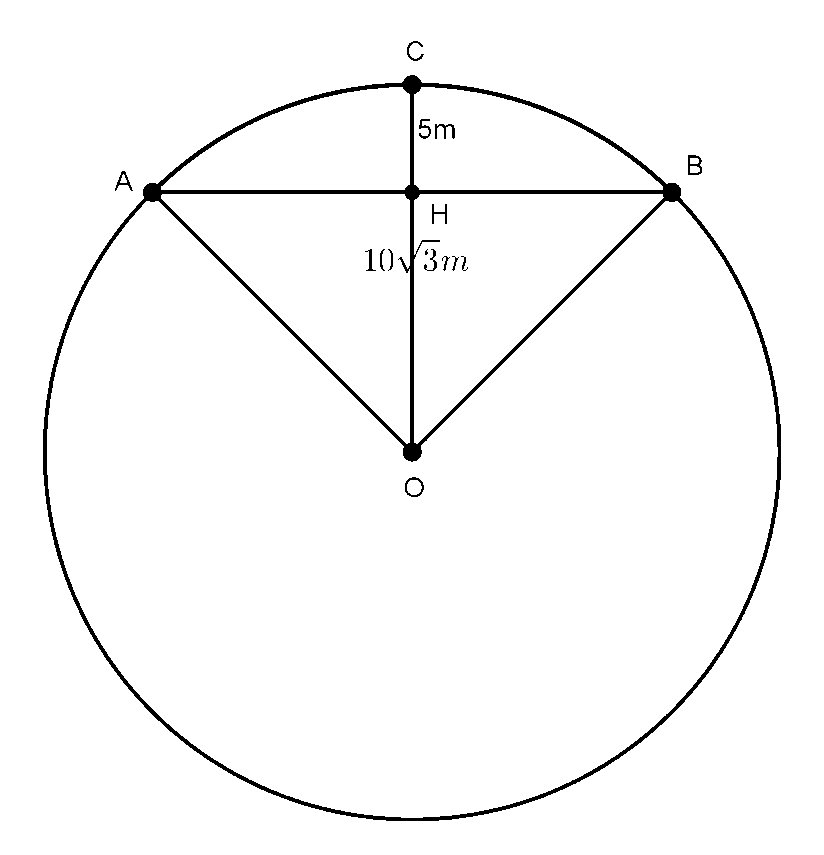
Ảnh đính kèm

Gọi AB là dây cung tương ứng với chiều rộng của mặt cắt đường hầm, C là điểm trên cung nhỏ AB sao cho OC $⊥$ AB, H là giao điểm của AB và OC. Khi đó, ta có: H là trung điểm của AB.

$\Rightarrow A B = 10 \sqrt{3} m,$ $C H = 5 m,$ $A H = B H = 5 \sqrt{3} m$

$\Rightarrow O H = C O - C H$ $= R - 5 (m)$

Xét $Δ O A H$ vuông tại H, có: $O A^{2} = O H^{2} + A H^{2}$ ( định lý Py – ta – go)

$\begin{array}{l} \Leftrightarrow R^{2} = {(R - 5)}^{2} + {(5 \sqrt{3})}^{2} \\ \Leftrightarrow R^{2} = R^{2} - 10 R + 25 + 75 \\ \Leftrightarrow - 10 R = - 100 \\ \Leftrightarrow R = 10 (m) \end{array}$

$\Rightarrow O H = 5 (m)$

Ta lại có:

$\sin \hat{H O A} = \frac{H A}{O A} = \frac{5 \sqrt{3}}{10} = \frac{\sqrt{3}}{2}$ $\Rightarrow \hat{H O A} = 60 °$ $\Rightarrow \hat{A O B} = 120 °$

Diện tích hình quạt AOB là:

$S_{1} = \frac{π {. 10}^{2} . 120}{360} = \frac{100 π}{3} (m^{2})$

Diện tích tam giác AOB là:

$S_{2} = \frac{1}{2} . A B . O H$ $= \frac{1}{2} . 10 \sqrt{3} . 5$ $= 25 \sqrt{3} (m^{2})$

Khi đó diện tích mặt cắt hầm là:

$S = S_{1} - S_{2}$ $= \frac{100 π}{3} - 25 \sqrt{3} (m^{2})$ .

Ví dụ 3: Cho hai đường tròn (O; 4cm) và (O’; 2cm) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài tiếp xúc (O) tại B và (O’) tại C. Tính diện tích phần gạch sọc biết BC =5cm và $\hat{A O B} = 60 °$

Ảnh đính kèm

Hướng dẫn giải

Diện tích hình thang OO’CB là:

$S_{1} = \frac{(O B + O' C) . B C}{2}$ $= \frac{(4 + 2) 5}{2} = 15 (c m^{2})$

Diện tích hình quạt OAB là:

$S_{2} = \frac{π {. 4}^{2} . 60}{360} = \frac{8}{3} π (c m^{2})$

Vì O’C//OB $\Rightarrow \hat{A O B} + \hat{A O' C} = 180 °$ (hai góc trong cùng phía bù nhau)

$\Rightarrow \hat{A O' C} = 120 °$

Diện tích hình quạt AO’C là:

$S_{3} = \frac{π {. 2}^{2} . 120}{360} = \frac{4}{3} π (c m^{2})$

Diện tích phần gạch sọc:

$S = S_{1} - S_{2} - S_{3}$ $= 15 - \frac{8}{3} π - \frac{4}{3} π$ $= 15 - 4 π (c m^{2})$

C. Bài tập tự luyện

Bài 1. Hãy tính diện tích hình viên phân AmB biết góc ở tâm $\hat{A O B} = 60^{0}$ và bán kính đường tròn là 5,1 cm.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập tính diện tích hình tròn và chu vi hình tròn cực hay, chi tiết

Xem thêm các chương trình khác: