Bài tập hai đường thẳng vuông góc trong đường tròn có lời giải chi tiết

191 lượt xem

Bài trước

Bài sau

CHỨNG MINH HAI ĐƯỜNG THẲNG VUÔNG GÓC

A. Kiến thức cần nhớ

Để chứng minh hai đường thẳng vuông góc với nhau, ta có các cách sau:

- Hai đường thẳng đó cắt nhau và tạo ra một góc 90.

- Hai đường thẳng đó chứa hai tia phân giác của hai góc kề bù.

- Hai đường thẳng đó chứa hai cạnh của tam giác vuông.

- Tính chất từ vuông góc đến song song: Có một đường thẳng thứ 3 vừa song song với đường thẳng thứ nhất vừa vuông góc với đường thẳng thứ hai.

- Sử dụng tính chất đường trung trực của đoạn thẳng. Tính chất: Mọi điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

- Sử dụng tính chất trực tâm của tam giác.

- Sử dụng tính chất đường phân giác, trung tuyến ứng với cạnh đáy của tam giác cân.

- Hai đường thẳng đó chứa hai đường chéo của hình vuông, hình thoi.

- Sử dụng tính chất đường kính và dây cung trong đường tròn.

- Sử dụng tính chất tiếp tuyến trong đường tròn

B. Ví dụ minh họa

Ví dụ 1. Cho hai đường tròn $(O_{1})$ và $(O_{2})$ cắt nhau tại A và B. Đường thẳng $O_{1} A$ cắt $(O_{2})$ tại C, đường thẳng $O_{2} A$ cắt $(O_{1})$ tại D, đường thẳng qua B song song với AD cắt $(O_{1})$ tại E. Chứng minh rằng nếu DE song song với AC thì $O_{2} C$ vuông góc với CD.

Hướng dẫn giải

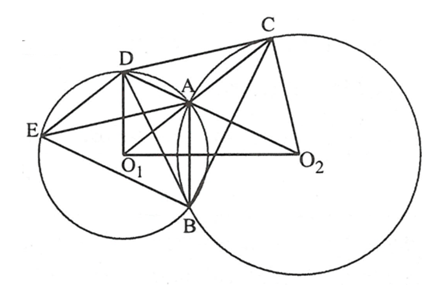
Ảnh đính kèm

Tứ giác $A B E D$ nội tiếp $\Rightarrow ∠ O_{2} A B = ∠ B E D$

$\Rightarrow ∠ A C B = \frac{1}{2} ∠ A O_{2} B = ∠ A O_{2} O_{1}$

$= 90 ° - ∠ O_{2} A B = 90 ° - ∠ B E D$

$∠ A B C = \frac{1}{2} ∠ A O_{2} C$ $= 90 ° - ∠ O_{2} A C$

$= 90 ° - ∠ O_{1} A D$

Theo giả thiết, BE song song AD và DE song song $O_{1} A$

$\Rightarrow ∠ O_{1} A D = ∠ B E D$ $\Rightarrow ∠ A B C = 90 ° - ∠ B E D$

$\Rightarrow ∠ A B C = ∠ A C B \Rightarrow$ tam giác $A B C$ cân tại $A \Rightarrow A B = A C$

Tứ giác $O_{1} D C O_{2}$ có $∠ C A O_{2} = ∠ D A O_{1}$ (đối đỉnh)

Mà tam giác $A D O_{1}$ và tam giác $A C O_{2}$ cân

$\Rightarrow ∠ A O_{1} D = ∠ A O_{2} C$ $\Rightarrow ∠ C O_{1} D = ∠ D O_{2} C \Rightarrow$ tứ giác $O_{1} D C O_{2}$ nội tiếp.

Mặt khác $∠ A O_{2} O_{1} = 90 ° - ∠ B E D$ và $∠ O_{1} D A = ∠ O_{1} A D = ∠ B E D$

$\Rightarrow ∠ D O_{2} O_{1} + ∠ O_{1} D O_{2}$ $= (90 ° - ∠ B E D) + ∠ B E D = 90 °$

$\Rightarrow ∠ D O_{1} O_{2} = 90 °$ $\Rightarrow ∠ D C O_{2} = 90 ° \Rightarrow O_{2} C$ vuông góc với CD

Ví dụ 2. Cho tứ giác $ABCD$ nội tiếp đường tròn. AC và BD cắt nhau tại $P, AD$ và BC cắt nhau tại Q thỏa mãn PQ vuông góc với AC. E là trung điểm AB. Chứng minh rằng PE vuông góc với BC.

Hướng dẫn giải

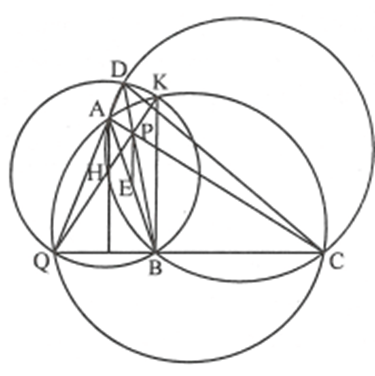
Ảnh đính kèm

Gọi K là giao điểm của đường tròn ngoại tiếp tam giác AQC và đường tròn ngoại tiếp tam giác QBD.

Tứ giác ABCD nội tiếp đường tròn, giao điểm của đường tròn $(ABCD)$ và đường tròn $(AQC)$ là A và C, giao điểm của $(ABCD)$ và đường tròn $(QBD)$ là B và D

$\Rightarrow Q, P, K$ thẳng hàng

$\Rightarrow ∠ DQK = ∠ DBK .$

$∠ ADB = ∠ ACB$ $\Rightarrow ∠ QDB = ∠ ACQ$

$\Rightarrow$ tam giác $QAC$ và tam giác $QBD$ đồng dạng (g.g) $\Rightarrow ∠ QAC = ∠ QBD .$

Theo giả thiết ta có $QP$ vuông góc với $AC,$

$\Rightarrow 90 ° = ∠ AQP + ∠ QAP$ $= ∠ PBK + ∠ QBD$

$\Rightarrow ∠ KBQ = 90 °$ hay KB vuông góc với BC

Gọi H là trực tâm tam giác $QAC \Rightarrow AH$ vuông góc với $QC, QP$ vuông góc với $AC \Rightarrow H$ nằm trên BK. Theo tính chất trực tâm tam giác thì $PH = PK .$

Theo giả thiết, $EA = EB \Rightarrow PE$ song song với $KB \Rightarrow PE$ vuông góc với BC

Ví dụ 3. Cho tam giác nhọn ABC. Tiếp tuyến tại B và C với đường tròn ngoại tiếp tam giác ABC cắt nhau tại P. Gọi D là điểm đối xứng của B qua AC, E là điểm đối xứng của C qua $AB, O$ là tâm đường tròn ngoại tiếp tam giác PDE. Chứng minh rằng AO vuông góc với BC.

Hướng dẫn giải

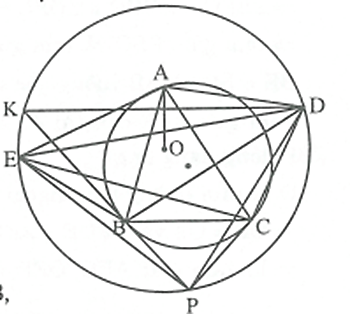
Ảnh đính kèm

Theo giả thiết tiếp tuyến tại B và C cắt nhau tại P

$\Rightarrow PB = PC$

D là điểm đối xứng của B qua AC, E là điểm đối xứng của C qua AB

$\begin{array}{l} \Rightarrow CD = CB \Rightarrow ∠ BCD = 2 ∠ ACB . \\ BE = BC \Rightarrow ∠ CBE = 2 ∠ ABC \\ ∠ PBC = ∠ PCB = ∠ BAC \\ \Rightarrow ∠ PCD = ∠ PCB + ∠ BCD \\ = ∠ BAC + 2 ∠ ACB, \\ ∠ PBE = 360 ° - ∠ PBC - ∠ CBE \\ = 360 ° - ∠ BAC - 2 ∠ ABC \\ = 2 (∠ ABC + ∠ BCA + ∠ CAB) - ∠ BAC - \\ 2 ∠ ABC \\ = ∠ BAC + 2 ∠ ACB \end{array}$

$\Rightarrow ∠ PBE = ∠ PCD \Rightarrow$ tam giác PBE và tam giác PCD bằng nhau (c.g.c)

$\Rightarrow PE = PD \Rightarrow$ tam giác $PDE$ cân tại P $\Rightarrow ∠ PDE = ∠ PED$

$\Rightarrow$ hai tam giác cân $PBC, PED$ đồng dạng (g.g) $\Rightarrow ∠ PBC = ∠ PED .$

Gọi K là giao điểm của PB và đường tròn ngoại tiếp tam giác PDE

$\Rightarrow ∠ BKD = ∠ PED = ∠ PBC \Rightarrow BC$ song song với $KD \Rightarrow ∠ BAC = ∠ BKD .$

Theo giả thiết $CB = CD$ và AC vuông góc với $BD \Rightarrow AB = AD$

$\Rightarrow ∠ BAC = ∠ CAD$ $\Rightarrow ∠ BAD = 2 ∠ BAC = 2 ∠ BKD$

$\Rightarrow A$ là tâm của đường tròn ngoại tiếp tam giác $DKB .$

O là tâm đường tròn ngoại tiếp tam giác $PDK \Rightarrow O$ và A nằm trên trung trực $DK \Rightarrow AO$ vuông góc DK. Mà DK song song $BC \Rightarrow AO$ vuông góc với BC

C. Bài tập tự luyện

Bài 1. Cho đường tròn tâm $(O)$ và dây cung AB. M là điểm trên AB. Đường tròn $(O_{1})$ qua A, M tiếp xúc với $(O)$ , đường tròn tâm $(O_{2})$ qua M, B và tiếp xúc với $(O)$ . Hai đường tròn $(O_{1})$ và $(O_{2})$ cắt nhau tại điểm tại điểm thứ hai là N. Chứng minh rằng tam giác MON vuông.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập hai đường thẳng vuông góc trong đường tròn có lời giải chi tiết

Xem thêm các chương trình khác: