CHỨNG MINH BA ĐIỂM THẲNG HÀNG
A. Phương pháp giải
+ Chứng minh một điểm thuộc đường thẳng chứa hai điểm còn lại
+ Chứng minh qua 3 điểm xác định được một góc bẹt
+ Chứng minh hai góc ở vị trí đối đỉnh mà bằng nhau
+ Chứng minh 3 điểm xác định được hai đường thẳng cùng vuông góc hay cùng song song với một đường thẳng thứ ba
+ Dùng tính chất đường trung trực
+ Dùng tính chất tia phân giác
+ Sử dụng tính chấy đồng quy của các đường: trung tuyến, phân giác, đường cao trong tam giác
+ Sử dụng tính chất đường chéo của các tứ giác đặc biiệt
+ Sử dụng tính chất tâm và đường kính của đường tròn
+ Sử dụng tính chất hai đường tròn tiếp xúc nhau
B. Ví dụ minh họa
Ví dụ 1: Cho đường tròn (O), đường kính AB. Lấy điểm C nằm giữa O và B, lấy điểm D trên đường tròn (O) sao cho AD = BC. Kẻ CH vuông góc với AD (H thuộc AD). Tia phân giác của góc DAB cắt đường tròn (O) tại điểm thứ hai E và cắt CH tại F. DF cắt đường tròn (O) tại điểm thứ hai N
a) Chứng minh CH // BD
b) Chứng minh tứ giác AFCN nội tiếp
c) Chứng minh ba điểm N, C, E thẳng hàng
Hướng dẫn giải
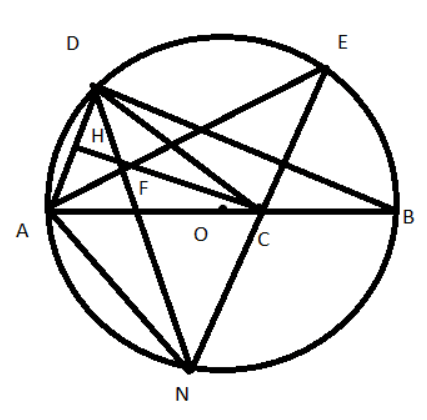
a) Có nhìn đường kính AB nên suy ra AD vuông góc với DB
+ Có CH vuông góc với AD (giả thiết)
Suy ra CH song song với BD (từ vuông góc đến song song)
b) suy ra (đồng vị)
lại có (cùng chắn cung AD)
Suy ra
+ Tứ giác AECN có:
Hai góc cùng nhìn một cạnh
Suy ra 4 điểm thuộc một đường tròn hay tứ giác AECN nội tiếp.
c) + Tứ giác AFCN nội tiếp đường tròn có (3) và
(4)
Ta có (2 góc ke bù)
Từ (4) và (5) suy ra:
+ Xét và
chung
Suy ra hai tam giác NAE đồng dạng với tam giác FCE
Suy ra hai góc ( 2 góc tương ứng bằng nhau) (6)
Từ (3) và (6) suy ra
Suy ra thẳng hàng.
Ví dụ 2: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Đường thẳng AO cắt (O) tại E và đường thẳng AO’ cắt (O’) tại F. Chứng minh rằng E, B, F thẳng hàng.
Hướng dẫn giải
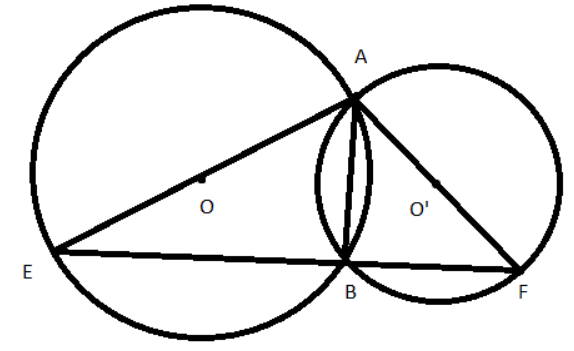
+ Có nhìn đường kính AE nên
+ Có nhìn đường kính AF nên
+ Có
Suy ra 3 điểm E, B, F thẳng hàng.
C. Bài tập tự luyện
Bài 1: Từ điểm S nằm ngoài đường tròn (O), vẽ tiếp tuyến SA (A là tiếp điểm) và cát tuyến SBC đến đường tròn (O) (A thuộc cung nhỏ BC). Gọi H là trung điểm của BC
a, Chứng minh SA2 = SB.SC và tứ giác SAHO nội tiếp đường tròn
b, Kẻ đường kính AK của (O). Tia SO cắt CK tại E. Chứng minh EK.BH = AB.OK
c, Tia AE cắt (O) tại D. Chứng minh ba điểm B, O, D thẳng hàng
Bài 2: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B (O và O’ nằm về hai phía đối với dây cung AB). Kẻ AC và AD thứ tự là đường kính của hai đường tròn (O) và (O’)
a, Chứng minh ba điểm C, B, D thẳng hàng
b, Đường thẳng AC cắt đường tròn (O’) tại E, đường thẳng AD cắt đường tròn (O) tại F (E, F khác A). Chứng minh tứ giác CDEFF nội tiếp đường tròn
Bài 3: Cho tam giác ABC có ba góc nhọn nội tiếp (O) (AB <AC). Các đường cao AD, BE và CF cắt nhau tại H
a, Chứng minh các tứ giác AEHF và ACD là các tứ giác nội tiếp
b, Gọi I là điểm dối xứng với E qua bC, BC cắt AI, EI lần lượt lại L và K. Vẽ LN vuông góc với AC tại N. Chứng minh
c, Chứng minh ba điểm F, D, I thẳng hàng
Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

