Bài tập sự tương giao giữa parabol và đường thằng cực hay, chi tiết (bài toán tính khoảng cách, diện tích, chu vi)

209 lượt xem

Bài trước

Bài sau

BÀI TOÁN TƯƠNG GIAO GIỮA PARABOL VÀ ĐƯỜNG THẲNG

BÀI TOÁN KHOẢNG CÁCH, TÍNH DIỆN TÍCH, CHU VI

A. Phương pháp giải

+) Đối với tính khoảng cách từ một điểm đến một đường thẳng, giữa hai điểm: Sử dụng hệ thức lượng trong tam giác vuông, hoặc định lý Py – ta – go để tính toán.

+) Tính diện tích: Sử dụng công thức tính diện tích tam giác, hình thang, hình chữ nhật, hình vuông, …

+) Tính chu vi: Sử dụng công thức tính chu vi để tính toán

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình: $y = \frac{1}{2} x^{2}$ và hai điểm A, B thuộc (P) có hoành độ lần lượt là $x_{A} = - 1$ , $x_{B} = 2$ .

a) Tìm tọa độ của hai điểm A, B.

b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.

c) Tính khoảng cách từ điểm O (gốc tọa độ) tới đường thẳng (d).

Hướng dẫn giải

a) Hai điểm A, B thuộc (P) có hoành độ lần lượt là $x_{A} = - 1$ , $x_{B} = 2$ nên ta có:

$x_{A} = - 1$ $\Rightarrow y_{A} = \frac{1}{2} {(- 1)}^{2} = \frac{1}{2}$ $\Rightarrow A = (- 1; \frac{1}{2})$

$\Rightarrow y_{A} = \frac{1}{2} {(2)}^{2} = 2$ $\Rightarrow B (2; 2)$

Vậy tọa độ của hai điểm $A = (- 1; \frac{1}{2})$ , $B (2; 2)$

b) Gọi phương trình đường thẳng (d) là: $y = ax + b$

Đường thẳng (d) đi qua hai điểm A, B nên ta có phương trình:

$\{\begin{cases} \frac{1}{2} = - a + b \\ 2 = 2 a + b \end{cases}$ $\Leftrightarrow \{\begin{cases} 3 a = \frac{3}{2} \\ 2 a + b = 2 \end{cases}$ $\Leftrightarrow \{\begin{cases} a = \frac{1}{2} \\ b = 1 \end{cases}$

Vậy phương trình đường thẳng (d) là:

$y = \frac{1}{2} x + 1$

c) Đường thẳng (d) cắt trục Oy tại điểm $C (0; 1)$ $\Rightarrow OC = 1$ .

Đường thẳng (d) cắt trục Ox tại điểm $D (- 2; 0)$ $\Rightarrow OD = 2$ .

Gọi OH là khoảng cách từ O tới đường thẳng (d).

Áp dụng hệ thức lượng về cạnh và đường cao trong tam giác vuông OCD, ta có:

$\frac{1}{{OH}^{2}} = \frac{1}{{OC}^{2}} + \frac{1}{{OD}^{2}}$ $\Leftrightarrow \frac{1}{{OH}^{2}} = \frac{1}{1^{2}} + \frac{1}{2^{2}}$ $\Leftrightarrow \frac{1}{{OH}^{2}} = \frac{5}{4}$ $\Rightarrow OH = \frac{2}{\sqrt{5}}$

Ví dụ 2: Cho hai đường thẳng $(d_{1})$ : $y = mx + 2$ và $(d_{2})$ : $y = (m - 2) x + 4$ .

a) Tìm m để $d_{1} ⊥ d_{2}$

b) Vẽ đồ thị của 2 hàm số trên với m vừa tìm được

c) Tính diện tích của tam giác tạo bởi 2 đường thẳng $d_{1}$ , $d_{2}$ và trục Ox khi $d_{1} ⊥ d_{2}$

Hướng dẫn giải

a) Để $d_{1} ⊥ d_{2}$ thì ta có:

$m (m - 2) = - 1$

$\Leftrightarrow m^{2} - 2 m + 1 = 0$ $\Leftrightarrow {(m - 1)}^{2} = 0$ $\Rightarrow m = 1$

Vậy $m = 1$ thì $d_{1} ⊥ d_{2}$ .

b) Với $m = 1$ ta có phương trình hai đường thẳng $(d_{1})$ và $(d_{2})$ như sau:

$(d_{1})$ : $y = x + 2$ và $(d_{2})$ : $y = - x + 4$

+) Vẽ đồ thị hàm số $y = x + 2$ .

Ta có:

Đồ thị đi qua điểm $A (- 2; 0)$

Và qua điểm $B (1; 3)$

+) Vẽ đồ thị hàm số $y = - x + 4$ .

Ta có:

Đồ thị đi qua điểm $C (4; 0)$

Và qua điểm $B (1; 3)$

Vậy đồ thị của 2 hàm số $(d_{1})$ và $(d_{2})$ như hình bên.

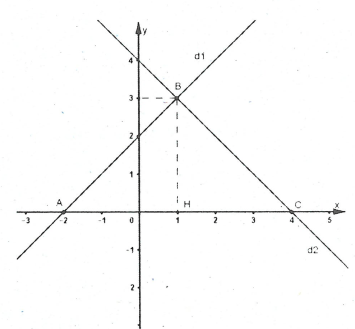
Ảnh đính kèm

c) Diện tích của tam giác tạo bởi 2 đường thẳng $d_{1}$ , $d_{2}$ và trục Ox khi $d_{1} ⊥ d_{2}$ , chính là diện tích tam giác ABC vuông tại B.

$\Rightarrow S_{ΔABC} = \frac{1}{2} BA . BC$

+) Với $BA = \sqrt{{BH}^{2} + {HA}^{2}}$ $= \sqrt{3^{2} + 3^{2}} = 3 \sqrt{2}$

$BC = \sqrt{{BH}^{2} + {HC}^{2}}$ $= \sqrt{3^{2} + 3^{2}} = 3 \sqrt{2}$

Vậy: $S_{ΔABC} = \frac{1}{2} BA . BC$ $= \frac{1}{2} . 3 \sqrt{2} . 3 \sqrt{2} = 9$

Vậy diện tích của tam giác tạo bởi 2 đường thẳng $d_{1}$ , $d_{2}$ và trục Ox khi $d_{1} ⊥ d_{2}$ là 9 (đvdt)

C. Bài tập tự luyện

Bài 1.

1) Cho parabol $(P) : y = \frac{1}{4} x^{2}$ và đường thẳng $d : y = - \frac{1}{2} x + 2$ .

a) Tìm tọa độ giao điểm của $(P)$ và d bằng phép tính.

b*) Gọi A và B là các giao điểm chung của $(P)$ và d . Tính diện tích tam giác OAB.

2) Cho parabol $(P) : y = - x^{2}$ và đường thẳng $d : y = - 3 x + 2$ .

a) Tìm tọa độ giao điểm của $(P)$ và d bằng phép tính.

b*) Gọi M và N là các giao điểm chung của $(P)$ và d . Tính diện tích tam giác OMN.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập sự tương giao giữa parabol và đường thằng cực hay, chi tiết (bài toán tính khoảng cách, diện tích, chu vi)

Xem thêm các chương trình khác: