Bài tập về tỉ số lượng giác của góc nhọn có đáp án

203 lượt xem

Bài trước

Bài sau

HỆ THỨC GIỮA CÁC TỈ SỐ LƯỢNG GIÁC CỦA CÁC GÓC $α$ VÀ $2 α$ $(0 ° < α < 45 °)$

A. Đặt vấn đề

Trong chuyên đề này ta sẽ thiết lập các hệ thức liên hệ giữa các tỉ số lượng giác của góc $α$ và góc $2 α$ . Nhờ đó mà ta tính được các tỉ số lượng giác của góc $α$ khi biết tỉ số lượng giác của góc $2 α$ và ngược lại.

B. Một số ví dụ

Ví dụ 1. Cho $α < 45 °$ , chứng minh rằng $\sin 2 α = 2 \sin α \cos α$

Áp dụng: Cho $\sin α = 0, 6$ tính $\sin 2 α$

Giải

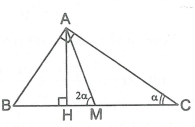
Ảnh đính kèm

Xét $Δ A B C$ vuông tại A, $\hat{C} < 45 °$

Vẽ đường cao AH và đường trung tuyến AM.

Khi đó

$M A = M B = M C = \frac{1}{2} B C$

Ta có $Δ A M C$ cân tại M, do đó

$\hat{A M B} = 2 \hat{C} = 2 α$

$Δ A B C$ vuông tại A, ta có $\sin α = \frac{A B}{B C}$ ; $\cos α = \frac{A C}{B C}$

Xét $Δ A H M$ vuông tại H, ta có $\sin 2 α = \frac{A H}{A M}$ $(1)$

Ta có

$2 \sin α . \cos α = 2 \frac{A B}{B C} . \frac{A C}{B C}$ $= \frac{2 . A B . A C}{B C^{2}}$ $= \frac{2 A H . B C}{B C^{2}}$ $= \frac{2 A H}{B C}$ $= \frac{2 A H}{2 A M}$ $= \frac{A H}{A M}$ $(2)$

Từ $(1)$ và $(2)$ suy ra

$\sin 2 α = 2 \sin α \cos α$

Áp dụng: Nếu $\sin α = 0, 6$ thì $\cos^{2} α = 1 - \sin^{2} α$ $= 1 - {(0, 6)}^{2} = 0, 64$

Do đó $\cos α = \sqrt{0, 64} = 0, 8$ .

Vậy $\sin 2 α = 2 \sin α . \cos α$ $= 2.0, 6.0, 8 = 0, 96$

Ví dụ 2. Cho $α < 45 °$ . Chứng minh các hệ thức sau:

a) $\cos 2 α = \cos^{2} α - \sin^{2} α$

b) $\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}$

Giải

a) Ta có

$\cos^{2} 2 α = 1 - \sin^{2} 2 α$ $= 1 - {(2 \sin α \cos α)}^{2}$ $= 1 - 4 \sin^{2} α \cos^{2} α$

$= {(\cos^{2} α + \sin^{2} α)}^{2} - 4 \sin^{2} α \cos^{2} α$

$= \cos^{4} α - 2 \sin^{2} α \cos^{2} α + \sin^{4} α$

$= {(\cos^{2} α - \sin^{2} α)}^{2}$

Do đó:

$\cos 2 α = \sqrt{{(\cos^{2} α - \sin^{2} α)}^{2}}$

$= |\cos^{2} α - \sin^{2} α|$

Vì $α < 45 °$ nên $\sin α < \cos α$ (xem bài 2.26).

Vậy $\cos 2 α = \cos^{2} α - \sin^{2} α$

Lưu ý: Tiếp tục biến đổi các hệ thức trên ta được các hệ thức sau

$\cos^{2} α - \sin^{2} α$ $= \cos^{2} α - (1 - \cos^{2} α)$ $= 2 \cos^{2} α - 1$

$\cos^{2} α - \sin^{2} α$ $= (1 - \sin^{2} α) - \sin^{2} α$ $= 1 - 2 \sin^{2} α$

Vậy $\cos 2 α = \cos^{2} α - \sin^{2} α$ $= 2 \cos^{2} α - 1 = 1 - 2 \sin^{2} α$

b) Ta có $\tan 2 α = \frac{\sin 2 α}{\cos 2 α}$ $= \frac{2 \sin α \cos α}{\cos^{2} α - \sin^{2} α}$

Chia cả tử và mẫu cho $\cos^{2} α$ ta được:

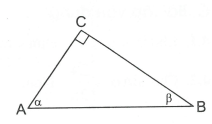
Ảnh đính kèm

$\tan 2 α = \frac{2 \sin α \cos α}{\cos^{2} α} : \frac{\cos^{2} α - \sin^{2} α}{\cos^{2} α}$ $= \frac{2 \sin α}{\cos α} : (1 - \tan^{2} α)$ $= \frac{2 \tan α}{1 - \tan^{2} α}$

Ví dụ 3. Cho tam giác ABC vuông tại C, $\hat{A} = α$ , $\hat{B} = β$ với $α < β$ .

Chứng minh rằng: ${(\sin α + \sin β)}^{2} = 1 + \sin 2 α$

Giải

$Δ A B C$ vuông tại C nên $\hat{A} + \hat{B} = 90 °$

Mặt khác, $\hat{A} < \hat{B}$ nên $\hat{A} = α < 45 °$

Ta có $α + β = 90 °$ nên $\sin β = \cos α$

Do đó ${(\sin α + \sin β)}^{2} = {(\sin α + \cos α)}^{2}$

$= \sin^{2} α + \cos^{2} α + 2 \sin α . \cos α$ $= 1 + \sin 2 α$

Ví dụ 4. Không dùng máy tính hoặc bảng số hãy tính:

$\sin 22 ° 30'$ , $\cos 22 ° 30'$ , $\tan 22 ° 30'$

Giải

Ta có $\cos 2 α = 1 - 2 \sin^{2} α$ $\Rightarrow \sin^{2} α = \frac{1 - \cos 2 α}{2}$

Với $α = 22 ° 30'$ , $2 α = 45 °$ ta được:

$\sin^{2} 22 ° 30' = \frac{1 - \cos 45 °}{2}$ $= \frac{1}{2} (1 - \frac{\sqrt{2}}{2})$ $= \frac{1}{2} . \frac{2 - \sqrt{2}}{2}$ $= \frac{2 - \sqrt{2}}{4}$

Suy ra $\sin 22 ° 30' = \frac{\sqrt{2 - \sqrt{2}}}{2}$

Ta có $\cos 2 α = 2 \cos^{2} α - 1$ $\Rightarrow \cos^{2} α = \frac{1 + \cos 2 α}{2}$

Với $α = 22 ° 30'$ , $2 α = 45 °$ ta được:

$\cos 22 ° 30' = \frac{1 + \cos 45 °}{2}$ $= \frac{1}{2} (1 + \frac{\sqrt{2}}{2})$ $= \frac{1}{2} . \frac{2 + \sqrt{2}}{2}$ $= \frac{2 + \sqrt{2}}{4}$

Suy ra $\cos 22 ° 30' = \frac{\sqrt{2 + \sqrt{2}}}{2}$

$\tan 22 ° 30' = \frac{\sin 22 ° 30'}{\cos 22 ° 30'}$ $= \frac{\sqrt{2 - \sqrt{2}}}{2} : \frac{\sqrt{2 + \sqrt{2}}}{2}$ $= \sqrt{\frac{2 - \sqrt{2}}{2 + \sqrt{2}}} = \sqrt{\frac{\sqrt{2} (\sqrt{2} - 1)}{\sqrt{2} (\sqrt{2} + 1)}}$ $= \sqrt{\frac{{(\sqrt{2} - 1)}^{2}}{1}} = \sqrt{2} - 1$

C. Bài tập vận dụng

4.1. Cho $0 ° < α < 45 °$ , chứng minh rằng $\sqrt{1 + \sin 2 α} = \sin α + \cos α$

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập về tỉ số lượng giác của góc nhọn có đáp án

Xem thêm các chương trình khác: