Bài tập chứng minh đường thẳng tiếp tuyến đường tròn cực hay, chi tiết

222 lượt xem

Bài trước

Bài sau

CHỨNG MINH MỘT ĐƯỜNG THẲNG LÀ TIẾP TUYẾN CỦA MỘT ĐƯỜNG TRÒN

A. Phương pháp giải

+) Phương pháp chứng minh đường thẳng d là tiếp tuyển của đường tròn (O; R):

– Cách 1: Nếu d và (O;R) có một điểm chung. Ta cần chứng minh đường thẳng d vuông góc với bán kính của đường tròn.

– Cách 2: Nếu d vuông góc với bán kính. Chứng minh khoảng cách từ tâm O của đường tròn đến đường thẳng d bằng bán kính R của đường tròn.

+) Sử dụng các tính chất của tiếp tuyến, hai tiếp tuyến cắt nhau, góc tạo bởi tia tiếp tuyến và dây cung để chứng minh các hệ thức về góc, hệ thức về cạnh, ...

B. Ví dụ minh họa

Ví dụ 1: Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA² = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).

Hướng dẫn giải

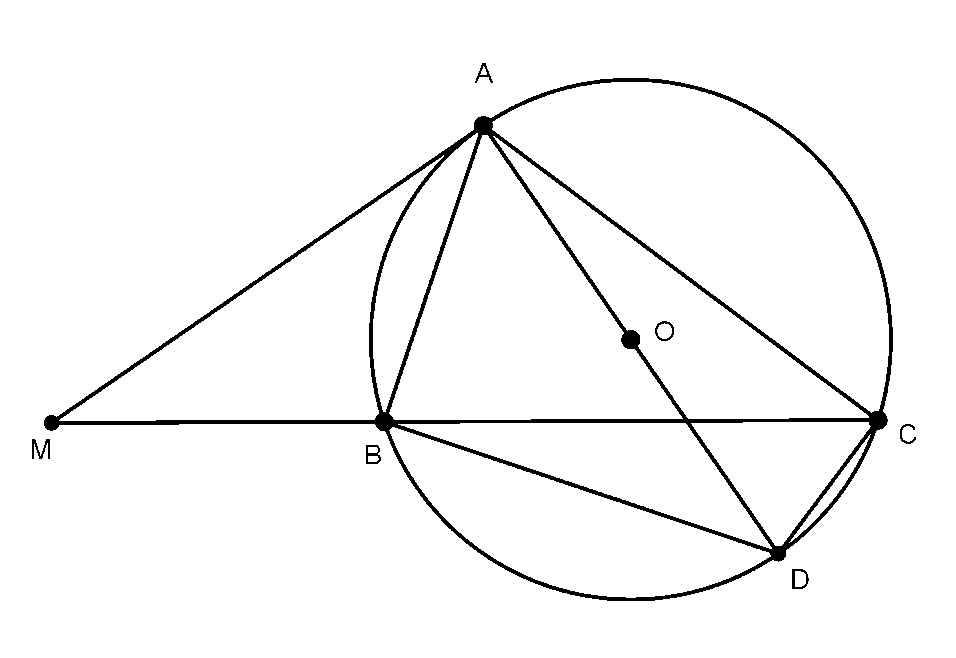
Ảnh đính kèm

Vì MA² = MB.MC

$\Rightarrow \frac{M A}{M B} = \frac{M C}{M A}$

Xét ΔMAC và ΔMBA có

$\hat{M}$ : góc chung

$\frac{M A}{M B} = \frac{M C}{M A}$

$\Rightarrow$ ΔMAC ∼ ΔMBA (c.g.c)

$\Rightarrow \hat{M A B} = \hat{M C A}$ (1)

Kẻ đường kính AD của (O)

Ta có: $\hat{A C B} = \hat{A D B}$ (hai góc nội tiếp cùng chắn cung AB )

Mà $\hat{M A B} = \hat{M C A}$ (chứng minh trên)

Suy ra $\hat{M A B} = \hat{A D B}$ (3)

Lại có $\hat{A B D} = 90 °$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \hat{B A D} + \hat{B D A} = 90 °$ (4)

Từ (3) và (4) suy ra $\hat{B A D} + \hat{M A B} = 90 °$ hay $\hat{M A O} = 90 °$

$\Rightarrow$ OA ⊥ MA

Do A ∈ (O)

$\Rightarrow$ MA là tiếp tuyến của (O).

Ví dụ 2: Cho đường tròn tâm O đường kính AB. C là một điểm thay đổi trên đường tròn (O). Tiếp tuyến tại C của (O) cắt AB tại D. Đường thẳng qua O và vuông góc với phân giác của $\hat{O D M}$ , cắt CD tại M. Qua M kẻ đường thẳng d song song với AB. Chứng minh d là tiếp tuyến của (O).

Hướng dẫn giải

Ảnh đính kèm

Kẻ OH $⊥$ d $\Rightarrow \hat{O H M} = 90 °$

Ta có CD là tiếp tuyến của (O) nên $O C ⊥ C D$ tại C $\Rightarrow \hat{O C M} = 90 °$

Gọi E là giao điểm của tia phân giác $\hat{O D M}$ với OM

Xét tam giác MDO có: DE là phân giác $\hat{O D M}$ , DE là đường cao

$\Rightarrow Δ D O M$ cân tại D

$\Rightarrow \hat{D M O} = \hat{D O M}$ (hai góc ở đáy)

Ta lại có : d//AB $\Rightarrow \hat{H M O} = \hat{D O M}$ (hai góc so le trong)

$\Rightarrow \hat{H M O} = \hat{D M O}$

Xét $Δ O H M$ và $Δ O C M$ , có:

$\hat{O H M} = \hat{O C M} = 90 °$

OM: cạnh chung

$\hat{H M O} = \hat{D M O}$ (cmt)

$\Rightarrow Δ O H M = Δ O C M$ (cạnh huyền – góc nhọn)

$\Rightarrow O H = O C = R$ (hai cạnh tương ứng)

$\Rightarrow H \in (O; R)$

Do đó d là tiếp tuyến của (O;R).

Ví dụ 3: Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC, cắt AB,AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm của AI. Chứng minh MF là tiếp tuyến của (O).

Hướng dẫn giải

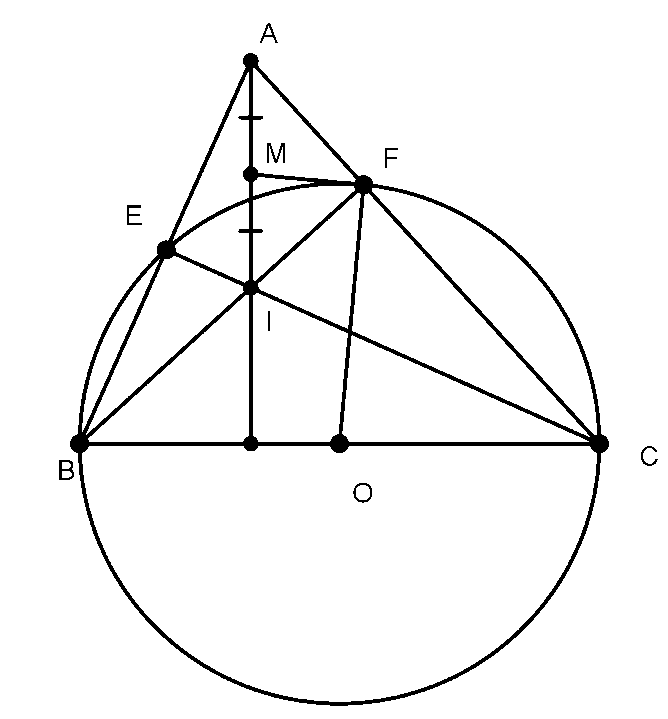
Ảnh đính kèm

Ta có: $\hat{B F C} = \hat{B E C} = 90 °$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow B F ⊥ A C, C E ⊥ A B$

Xét tam giác ABC, có $B F \cap C E = \{I\}$

$\Rightarrow$ I là trực tâm tam giác ABC

Gọi H là giao điểm của AI với BC

$\Rightarrow A I ⊥ B C$ tại H

Xét tam giác AFI vuông tại F, có M là trung điểm của AI

$\Rightarrow F M = M A = M I$

$\Rightarrow Δ F M A$ cân tại M

$\Rightarrow \hat{M A F} = \hat{M F A}$ (hai góc ở đáy) (1)

Xét tam giác OFC, có OF=OC

$\Rightarrow F O C$ cân tại O

$\Rightarrow \hat{O F C} = \hat{O C F}$ (hai góc ở đáy) (2)

Xét tam giác AHC vuông tại H, có: $\hat{MAF} + \hat{O C F} = 90 °$ (hai góc phụ nhau)(3)

Từ (1), (2) và (3)

$\Rightarrow \hat{MFA} + \hat{O F C} = 90 °$

Mà $\hat{M F O} + \hat{MFA} + \hat{O F C} = 180 °$

$\Rightarrow \hat{M F O} = 90 °$

$\Rightarrow M F ⊥ O F$

Vậy MF là tiếp tuyến của (O).

C. Bài tập tự luyện

Bài 1. Cho tam giác ABC có $A B = 3,$ $A C = 4,$ $B C = 5 .$ Vẽ $(B; B A) .$ Chứng minh rằng AC là tiếp tuyến của đường tròn.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập chứng minh đường thẳng tiếp tuyến đường tròn cực hay, chi tiết

Xem thêm các chương trình khác: