Bài tập tính thể tích các hình hỗn hợp có đáp án

175 lượt xem

Bài trước

Bài sau

TÍNH THỂ TÍCH CÁC HÌNH HỖN HỢP

A. Phương pháp giải

Phân cắt hình đã cho thành các hình quen thuộc như hình trụ, hình nón, hình nón cụt, hình cầu để tính toán.

B. Vi dụ minh họa

Ví dụ 1. Hãy tính thể tích, diện tích bề mặt các chi tiết máy theo kích thước đã cho trên hình vẽ.

Hướng dẫn giải

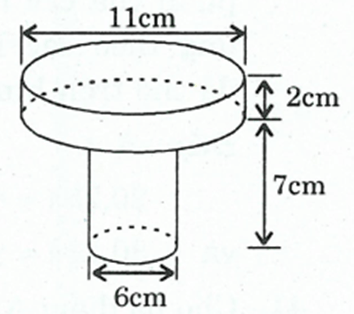
Ảnh đính kèm

Diện tích cần tính gồm diện tích xung quanh hai hình trụ và diện tích hai hình tròn.

-Hình trụ thứ nhất có đường kính đáy 11cm và chiều cao 2cm, có diện tích:

$S_{1} = π . 11.2 = 22 π (c m^{2})$

- Hình trụ thứ hai có đường kính đáy 6cm và chiều cao 7cm, có diện tích:

$S_{2} = π . 6.7 = 42 π (c m^{2})$

- Phần còn lại có liên quan đến

+ Một hình tròn bán kính đáy 5,5cm.

+ Một hình vành khăn bán kính lớn là 5,5cm và bán kính nhỏ là 3cm.

+ Một hình tròn có bán kính 3cm.

Tổng diện tích các hình tròn này thì bằng 2 lần diện tích hình tròn bán kính 5,5cm:

$S_{3} = π . {(5, 5)}^{2} + π . (5, 5^{2} - 3^{2}) + π 3^{2}$ $= 2 π {(5, 5)}^{2}$ $= 60, 5 . π$

Diện tích chi tiết máy là

$22 π + 42 π + 60, 5 π = 124, 5 π$ $\approx 390, 93 \Rightarrow S \approx 391 (c m^{2})$

Thể tích của chi tiết là

$π . {(5, 5)}^{2} . 2 + π . 3^{2} . 7$ $= 123, 5 π$

$\Rightarrow V \approx 387, 79$ hay $V \approx 388 c m^{3}$

Ví dụ 2. Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R. GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (hình bên). Cho hình vẽ quay xung quanh trục GO. Chứng minh rằng:

a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.

b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.

Hướng dẫn giải

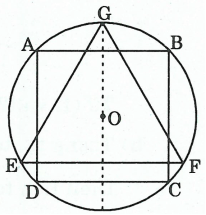
Ảnh đính kèm

a) Gọi r là bán kính đường tròn ngoại tiếp, ta có:

- Cạnh hình vuông: $A B = A D = r \sqrt{2}$

- Cạnh tam giác đều: $E F = r \sqrt{3}$ .

Khi quay xung quanh GO, hình vuông tạo thành một hình trụ

có bán kính đáy: $R = \frac{1}{2} A B - \frac{r \sqrt{2}}{2}$ ;

chiều cao: $h = A D = r \sqrt{2}$

Thể tích: $V_{1} = π {(\frac{r \sqrt{2}}{2})}^{2} . r \sqrt{2}$ $= \frac{π r^{3} \sqrt{2}}{2}$

Khi quay xung quanh GO, tam giác đều GEF tạo thành hình nón có bán kính đáy:

$R' = \frac{1}{2} E F = \frac{r \sqrt{3}}{2}$ .

Chiều cao bằng chiều cao tam giác đều GEF

$h' = r \sqrt{3} . \frac{\sqrt{3}}{2} = \frac{3 r}{2}$

Thể tích: $V_{2} = \frac{1}{3} π R'^{2} h'$ $= \frac{1}{2} π {(\frac{r \sqrt{3}}{2})}^{2} . \frac{3 r}{2}$ $= \frac{3}{8} π r^{3}$

Khi quay xung quanh GO, hình tròn tạo thành hình cầu bán kính r và:

Thể tích: $V_{3} = \frac{4}{3} π r^{3}$ .

Ta có: $V_{1}^{2} = {(\frac{π r^{3} \sqrt{2}}{2})}^{2}$ $= \frac{π^{2} r^{6}}{2}$ $(1)$

$V_{2} . V_{3} = \frac{3}{8} π r^{3} . \frac{4}{3} π r^{3}$ $= \frac{π^{2} r^{6}}{2}$ $(2)$

Từ $(1)$ và $(2)$ suy ra:

$V_{1}^{2} = V_{2} . V_{3}$ .

b) Tương tự, ta có diện tích toàn phần hình trụ:

$S_{1} = 3 π r^{2}$

Diện tích toàn phần hình nón:

$S_{2} = \frac{9}{4} π r^{2}$

Diện tích mặt cầu: $S_{3} = 4 π r^{2}$ .

Từ đây ta có:

$S_{1}^{2} = {(3 π r^{2})}^{2} = 9 π^{2} r^{4}$

$S_{2} . S_{3} = \frac{9}{4} π r^{2} . 4 π r^{2}$ $= 9 π^{2} r^{4}$

Vậy: $S_{1}^{2} = S_{2} . S_{3}$ .

C. Bài tập tự luyện

Bài 1. Một khối gỗ dạng hình trụ, bán kính đáy là R chiều cao 2R (đơn vị cm). Người ta khoét rỗng hai nửa hình cầu như hình bên. Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập tính thể tích các hình hỗn hợp có đáp án

Xem thêm các chương trình khác: