Các bài toán hệ thức lượng trong tam giác vuông nâng cao có ví dụ minh họa

230 lượt xem

Bài trước

Bài sau

MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG

A. Kiến thức cần nhớ

1. Định lí

Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

• Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;

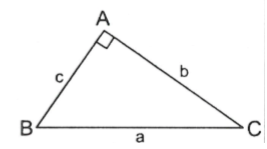
Ảnh đính kèm

• Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề

Trong hình bên thì:

$\begin{array}{l} b = a \sin B = a \cos C; c = a \sin C = a \cos B \\ b = c \tan B = c \cot C; c = b \tan C = b \cot B \end{array}$

2. Giải tam giác vuông

Là tìm tất cả các cạnh và góc của tam giác vuông B khi biết hai yếu tố của nó (trong đó ít nhất có một yếu tố về độ dài).

B. Một số ví dụ

Ví dụ 1. Cho tam giác ABC vuông tại A, đường cao AH, $\hat{B} = α$ . Tính giá trị của a để BH = 3CH.

Giải

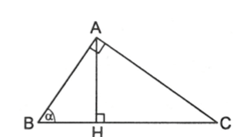
Ảnh đính kèm

Đặt AH = h.

Xét DABH vuông tại H ta có:

BH = AH.cot B = h.cot a.

Xét DACH vuông tại H ta có:

CH = AH.cot C = AH.tan B = h.tan a.

$\begin{array}{l} B H = 3 C H \Leftrightarrow h . \cot α = 3 h . \tan α \\ \Leftrightarrow \frac{1}{\tan α} = 3 \tan α \\ \tan^{2} α = \frac{1}{3} \Leftrightarrow \tan α \\ = \frac{\sqrt{3}}{3} = \tan 30 ° \\ \Leftrightarrow α = 30 ° \end{array}$

Nhận xét: Trong bài giải ta đã biểu diễn BH và CH theo AH và theo một tỉ số lượng giác của góc a. Từ mối quan hệ giữa BH và CH ta tìm được giá trị của a.

Ví dụ 2. Giải tam giác ABC biết $\hat{B} = 35 °, \hat{C} = 50 °$ và đường cao AH = 5,0cm.

Giải

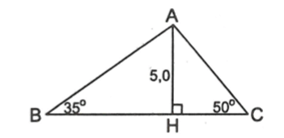
Ảnh đính kèm

Ta phải tìm $\hat{A}$ , AB, AC và BC.

$\hat{A} = 180 ° - (\hat{B} + \hat{C}) = 95 °$

• Xét DABH vuông tại H ta có:

$A H = A B . \sin B$ $\Rightarrow A B = \frac{A H}{\sin B} = \frac{5, 0}{\sin 35^{ο}} \approx 8, 7 c m$

$B H = A H . c o t B$ $\approx 5, 0 . c o t 35^{\circ} \approx 7, 1 c m$

• Xét DACH vuông tại H ta có:

$A H = A C . \sin C$ $\Rightarrow A C = \frac{A H}{\sin C} = \frac{5, 0}{\sin 50 °} \approx 6, 5 (c m)$

$C H = A H . \cot C$ $\approx 5, 0 . \cot 50 ° \approx 4, 2 (c m)$

Do đó

$B C = B H + C H$ $= 7, 1 + 4, 2 = 11, 3 (c m)$

Vậy $\hat{A} = 95 °; A B = 8, 7 c m;$ $A C = 6, 5 c m; B C = 11, 3 c m$

Ví dụ 3. Cho tam giác ABC, cạnh BC cố định. Biết BC = 4cm, AB + AC = 8cm. Tính giá trị lớn nhất của góc A.

Giải

Vẽ đường phân giác AD. Vẽ BH ^ AD và CK ^ AD.

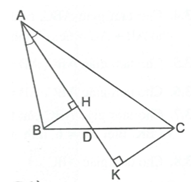
Ảnh đính kèm

Xét DABH vuông tại H, DACK vuông tại K, ta có:

$B H = A B . \sin \frac{A}{2}; C K = A C \sin \frac{A}{2}$

Vậy $B H + C K = (A B + A C) \sin \frac{A}{2} = 8 \sin \frac{A}{2}$

Mặt khác ,

$B H + C K \leq B D + C D = B C = 4 (c m)$

nên $8 \sin \frac{A}{2} \leq 4 \Rightarrow \sin \frac{A}{2} \leq \frac{1}{2} = \sin 30 °$

Do đó $\frac{\hat{A}}{2} \leq 30 ° \Rightarrow \hat{A} \leq 60 °$

vậy $\max \hat{A} = 60 °$ khi D, H, K trùng nhau Û DABC đểu.

Ví dụ 4. Chứng minh định lí côsin: Trong một tam giác nhọn, bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia trừ đi hai lần tích của hai cạnh ấy với côsin của góc xen giữa của chúng.

Giải

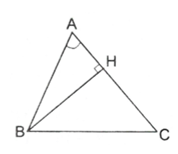
Ảnh đính kèm

Vẽ đường cao BH. Xét DHBC vuông tại H ta có:

$\begin{array}{l} B C^{2} = H B^{2} + H C^{2} \\ = H B^{2} + {(A C - A H)}^{2} \\ = H B^{2} + A C^{2} - 2 A C . A H + A H^{2} \\ = (H B^{2} + A H^{2}) + A C^{2} - 2 A C . A H \\ = A B^{2} + A C^{2} - 2 A C . A H (1) \end{array}$

Xét DABH vuông tại H ta có : AH = AB. cosA

Thay vào (1) ta được

$B C^{2} = A B^{2} + A C^{2} - 2 A C . A B . c o s A$

Nhận xét: Trong một tam giác nhọn, nếu biết hai cạnh và góc xen giữa thì nhờ định lí côsin ta có thế tính được cạnh thứ ba.

C. Bài tập vận dụng

• Vận dụng hệ thức về cạnh và góc trong tam giác vuông để chứng minh hoặc tính toán

3.1. Cho tam giác nhọn ABC. Vẽ các đường cao AD, BE, CF. Chứng minh rằng:

a) AD.BE.CF = AB.BC.CA.sin A.sin B.sin C;

b) AE.BF.CD = AB.BC.CA.cos A.cos B.cos C.

3.2. Cho tam giác nhọn ABC. Vẽ các đường cao AA', BB', CC’. Chứng minh rằng:

$A B' . B C' . C A' = A' B . B' C . C' A$ $= A B . B C . C A . \cos A . \cos B . \cos C$

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Các bài toán hệ thức lượng trong tam giác vuông nâng cao có ví dụ minh họa

Xem thêm các chương trình khác: