Bài tập sự xác định đường tròn. Tính chất đối xứng của đường tròn

181 lượt xem

SỰ XÁC ĐỊNH ĐƯỜNG TRÒN

TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN

I. LÝ THUYẾT

· Đường tròn tâm O bán kính R (với R > 0) là hình gồm các điểm cách O một khoảng bằng R. Ta kí hiệu đường tròn tâm O bán kính R là (O;R).

· Qua ba điểm không thẳng hàng ta vẽ được một và chỉ một đường tròn.

· Trong một tam giác vuông, trung điểm của cạnh huyền là tâm của đường tròn ngoại tiếp tam giác vuông đó.

· Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác thì đó là tam giác vuông

· Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.

· Đường tròn là hình có trục đối xứng. Bất kì đường thẳng nào qua tâm đường tròn cũng là trục đối xứng của đường tròn.

II. BÀI TẬP VẬN DỤNG

Bài 1. Hình vẽ:

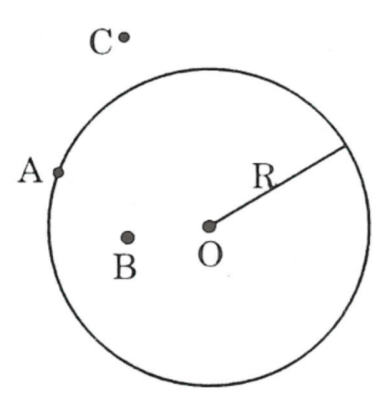
Ảnh đính kèm

Cho đường tròn tâm O bán kính R. Gọi A là điểm nằm trên đường tròn, B nằm trong đường tròn; C nằm ngoài đường tròn. Hãy điền dấu >, < hoặc = vào ô trống:

Bài 2. Cho đường tròn tâm O bán kính 3cm, điểm M nằm ngoài đường tròn, điểm N nằm trong đường tròn. Hãy so sánh độ dài OM và ON.Cho đoạn thẳng $A B = 6 c m$ . Hãy vẽ hai đường tròn tâm $O$ và $O^{'}$ qua hai điểm A, B. Có nhận xét gì về quan hệ giữa đường thẳng $O O^{'}$ và $A B$ ? Có thể vẽ được bao nhiêu đường tròn như vậy?

Bài 3. Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của hai đường trung trực của AB và BC. So sánh độ dài của OA, OB, OC. Vẽ đường tròn qua ba điểm A, B, C.

Bài 4. Cho tam giác MNP vuông tại M. Hãy vẽ đường tròn ngoại tiếp tam giác MNP.

Bài 5. Cho tam giác ABC vuông tại C có O là trung điểm của cạnh huyền AB. Từ O kẻ đường thẳng d vuông góc với CA. Chứng minh rằng đường thẳng d là trung trực của đoạn CA.Từ đó suy ra $O A = O B = O C$ .

Bài 6. Cho tam giác MNP nội tiếp đường tròn tâm O đường kính MN. Chứng minh rằng $O M = O N = O P$ . Từ đó suy ra góc MPN vuông.

Bài 7. Cho đường tròn (O), A là điểm nằm trên đường tròn. Tìm điểm $A^{'}$ đối xứng với $A$ qua tâm O. Lấy một điểm B khác A cũng thuộc đường tròn.

a) Tìm điểm $B^{'}$ đối xứng với $B$ qua tâm $O$ .

b) Có nhận xét gì về hai điểm $A^{'}$ và $B^{'}$ đối với đường tròn (O).

Bài 8. Cho đường tròn (O), d là đường thẳng đi qua tâm. Lấy M là điểm nằm trên đường tròn. Tìm điểm $M^{'}$ đối xứng của M qua d. Có nhận xét gì về giao điểm $M^{'}$ ? Hãy chứng minh điều này.

Bài 9. Cho tam giác MNP nội tiếp đường tròn đường kính MN. Vẽ điểm đối xứng của P qua trục đối xứng là đường kính MN.

Bài 10. Các phát biểu nào sau đây xác định duy nhất một đường tròn?

a) Đường tròn đi qua hai điểm cố định.

b) Đường tròn đi qua ba điểm không thẳng hàng.

c) Đường tròn có tâm O, bán kính 2cm.

d) Đường tròn đường kính AB cho trước.

Bài 11. Cho đường tròn tâm O, bán kính 5cm. Cho biết $O A = 3 c m, O B = 4 c m$ , $O C = 7 c m$ , $O D = 5 c m$ . Hãy cho biết mỗi điểm $A, B, C, D$ nằm trong, nằm trên hay nằm ngoài đường tròn.

Bài 12. Trên mặt phẳng tọa độ $O x y$ , hãy xác định vị trí tương đối của mỗi điểm $M (- 1; 1)$ , $N (\sqrt{2}; - \sqrt{2})$ , $P (1; - 2)$ đối với đường tròn $(O; 2)$ .

Bài 13. Cho đường tròn $(O; \sqrt{10} c m)$ . Cho biết $O I = 3 c m, O J = 4 c m, O K = \sqrt{10} c m$ . Hãy xác định vị trí tương đối của $I, J, K$ đối với đường tròn này.

Bài 14. Cho hình chữ nhật $A B C D$ có $A D = 18 c m, C D = 12 c m$ . Chứng minh rằng bốn điểm

$A, B, C, D$ cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Bài 15. Cho tam giác $A B C$ . Vẽ đường tròn $(O)$ đi qua B và C và tâm đường tròn nằm trên

AC. Khi nào thì tâm đường tròn $(O)$ trùng với điểm A?

Bài 16. Trên mặt phẳng tọa độ $O x y$ , cho đường tròn tâm O bán kính 3. Cho các điểm $A (0; 0), B (2; 3),$ $C (1; 5, 2), D (\sqrt{10}; 2)$

Hãy xác định vị trí các điểm $A, B, C, D$ đối với đường tròn $(O)$ .

Bài 17. Cho hình vuông $A B C D$ .

a) Chứng minh rẳng bốn đỉnh hình vuông nằm trên một đường tròn. Hãy chỉ rõ tâm của đường tròn đó.

b) Tính bán kính của đường tròn, biết cạnh hình vuông là 4cm.

Bài 18. Cho hình thang cân $A B C D (A B / / C D)$ . Chứng minh rằng bốn điểm $A, B, C, D$ cùng

thuộc một đường tròn. Xác định tâm O của đường tròn này.

Bài 19. Cho tam giác $A B C$ nhọn, hai đường cao $B E$ và $C F$ cắt nhau tại H.

a) Chứng minh rằng bốn điểm $B, F, E, C$ cùng thuộc một đường tròn.

b) Gọi O là trung điểm $A H$ . Chứng minh rằng $E, F$ thuộc dường tròn $(O; O A)$ .

Bài 20. Một tam giác vuông có cạnh góc vuông bằng 5 cm và 12 cm. Bán kính của một đường tròn ngoại tiếp tam giác đó là bao nhiêu?

Bài 21. Cho đường tròn (O), bán kính bằng 3. Trên mặt phẳng toạ độ Oxy, hãy xác định vị trí của mỗi điểm A, B, C đối với đường tròn (O), biết toạ độ của các điểm: $A (2, 2); B (- \sqrt{3}, \sqrt{6}), C (3, - \sqrt{6})$

Bài 22. Cho $Δ A B C$ gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Gọi O là tâm đường tròn đường kính NP

a) Đường tròn (O) có đi qua M và A không? Vì sao?

b) Đường tròn (O) cắt BC tại H. Đường thẳng AH có vai trò gì đôi với $Δ A B C$

Bài 23. Cho $Δ A B C$ , M là trung điểm của BC. Vẽ $M D ⊥ A B$ và $M E ⊥ A C$ . Trên các tia BD và CE lần lượt lấy các điểm I, K sao cho D là trung điểm của BI, E là trung điểm của CK.

a) Chứng minh bốn điểm B, I, K, C nằm trên cùng một đường tròn

b) Tam giác BIC và BKC là tam giác gì?

c) Gọi H là giao điểm của BK và CI. Chứng minh AH vuông góc với BC

Bài 24. Cho tam giác ABC, vuông tại A, đường cao AH. Biết $A H = 14 c m, H B = 7 c m$ . Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Bài 25. Cho tam giác ABC cân, có góc $\hat{A} = 120 °$ , nội tiếp đường tròn $(O; R)$ . Tính diện tích tam giác ABC theo R.

Bài 26. Cho tam giác đều ABC, trực tâm H, cạnh a:

a) Tâm của đường tròn ngoại tiếp tam giác ABC là điểm nào?

b) Tính bán kính của đường tròn đó theo a.

c) Gọi K là điểm đối xứng với H qua BC. Xác định vị trí tương đối của điểm K và đường tròn đó.

Bài 27. Trên các cạnh AB, BC, CD và DA của hình vuông ABCD ta lấy lần lượt các điểm E, F, G, H sao cho $A E = B F = C G = D H$ . Các đường chéo AC và BD cắt nhau ở O.

a) Chứng minh rằng ba điểm F, O, H thẳng hàng.

b) Chứng minh rằng O cách đều bốn điểm E, F, G, H.

c) Biết $\hat{B E C} = 60 °, B C = 6 c m$ , hãy tính BE.

Các dạng bài tập Toán 9

Bài tập sự xác định đường tròn. Tính chất đối xứng của đường tròn

Xem thêm các chương trình khác: