Bài tập tìm tâm và bán kính đường tròn có đáp án chi tiết

226 lượt xem

XÁC ĐỊNH TÂM, BÁN KÍNH VÀ CÁC ĐẠI LƯỢNG LIÊN QUAN ĐẾN ĐƯỜNG TRÒN NỘI TIẾP VÀ ĐƯỜNG TRÒN NGOẠI TIẾP

A. Phương pháp giải

+ Đa giác đều n cạnh có độ dài mỗi cạnh là a, R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp đa giác. Ta có:

$R = \frac{a}{2 . \sin \frac{180 °}{n}};$ $r = \frac{a}{2 . \tan \frac{180 °}{n}}$

+ Ngoài ra có thể sử dụng hệ thức lượng trong tam giác vuông, định lý Py – ta – go,… để tính R và r.

B. Ví dụ minh họa

Ví dụ 1: Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó

Hướng dẫn giải:

Ảnh đính kèm

Giả sử: OA = OB = R, OC = r

Ta có: $\hat{A O B} = \frac{360 °}{n}$

$\Rightarrow \hat{C O B} = \frac{\frac{360 °}{n}}{2} = \frac{180 °}{n}$

Trong tam giác COB, ta có: $\hat{O C B} = 90 °$

Nên $\sin \hat{C O B} = \frac{C B}{O B} = \frac{\frac{a}{2}}{R} = \frac{a}{2 R}$

$\Rightarrow 2 R = \frac{a}{\sin \frac{180 °}{n}}$ $\Leftrightarrow R = \frac{a}{2 \sin \frac{180 °}{n}}$ .

Ta lại có:

$\tan \hat{C O B} = \frac{C B}{O C} = \frac{\frac{a}{2}}{r} = \frac{a}{2 r}$

$\Rightarrow 2 r = \frac{a}{\tan \frac{180 °}{n}}$ $\Leftrightarrow r = \frac{a}{2 \tan \frac{180 °}{n}}$ .

Ví dụ 2: a) Vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).

Hướng dẫn giải

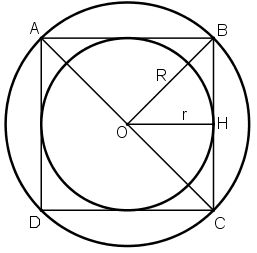
Ảnh đính kèm

a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).

c) Vẽ OH ⊥ BC.

$\Rightarrow$ OH là khoảng cách từ tâm O đến BC

Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)

$\Rightarrow$ O là tâm đường tròn nội tiếp hình vuông ABCD

OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.

Tam giác vuông OBC có OH là đường trung tuyến

$\Rightarrow O H = \frac{1}{2} B C = B H$ .

Xét tam giác vuông OHB có:

$r^{2} + r^{2} = O B^{2} = 2^{2}$ $\Leftrightarrow 2 r^{2} = 4$ $\Leftrightarrow r^{2} = 2$ $\Leftrightarrow r = \sqrt{2} (c m)$ .

Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

Ví dụ 3: a) Vẽ tam giác đều ABC cạnh a = 3cm.

b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.

c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.

d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).

Hướng dẫn giải

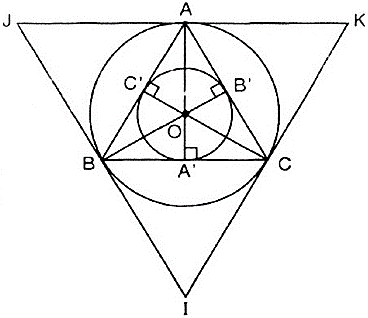
Ảnh đính kèm

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).

+ Dựng đoạn thẳng AB = 3cm.

+ Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b) * Vẽ đường tròn:

Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực cắt nhau tại O.

Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.

* Tính bán kính đường tròn.

+ Gọi A’ là trung điểm BC $\Rightarrow A' C = \frac{B C}{2} = \frac{a}{2} .$

và AA’ ⊥ BC

$\Rightarrow A A' = \sqrt{A C^{2} - A' C^{2}}$ $= \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = \frac{a \sqrt{3}}{2}$ .

+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến

$\Rightarrow$ Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến

Suy ra O là trọng tâm tam giác ABC.

$\Rightarrow O A = \frac{2}{3} A A' = \frac{2}{3} . \frac{a \sqrt{3}}{2}$ $= \frac{a}{\sqrt{3}} = \sqrt{3}$

Vậy R = $\sqrt{3}$ (cm).

c) * Vẽ đường tròn:

Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc $\hat{B A C};$ $\hat{A B C};$ $\hat{A C B} .$

Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.

Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.

* Tính r:

$r = O A' = \frac{1}{3} A A'$ $= \frac{1}{3} . \frac{a \sqrt{3}}{2}$ $= \frac{a}{2 \sqrt{3}}$ $= \frac{\sqrt{3}}{2}$

Vậy $r = \frac{\sqrt{3}}{2} .$

d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).

C. Bài tập tự luyện

Bài 1: Cho lục giác đều ABCDEF có tâm O. Đặt R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp lục giác. Viết biểu thức liên hệ giữa R và r.

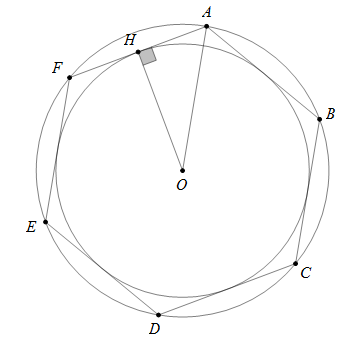
Ảnh đính kèm

Hướng dẫn giải

Lục giác đều ABCDEF nên chia đường tròn ngoại tiếp thành 6 cung bằng nhau, suy ra

$\hat{A O F} = \frac{360 °}{6} = 60 °$

Tam giác AOF cân tại O có $\hat{A O F} = 60 °$ nên $Δ A O F$ đều

Vẽ đường cao AH của $Δ A O F$

Khi đó $O H = r,$ $A H = \frac{R}{2}$

Xét $Δ A O H$ vuông tại H nên

$\begin{array}{l} A O^{2} = O H^{2} + A H^{2} \\ \Leftrightarrow R^{2} = r^{2} + {(\frac{R}{2})}^{2} \\ \Leftrightarrow r^{2} = \frac{3 R^{2}}{4} \\ \Leftrightarrow r = \frac{R \sqrt{3}}{2} . \end{array}$

Bài 2: Đường tròn nội tiếp hình vuông cạnh a có bán kính là

A. $a \sqrt{2}$ B. $\frac{a \sqrt{2}}{2}$ C. $\frac{a}{2}$ D. $\frac{a \sqrt{3}}{2}$

Hướng dẫn giải

Đáp án C

Áp dụng công thức: $r = \frac{a}{2 . \tan \frac{180 °}{4}} = \frac{a}{2}$ .

Bài 3: Cho tam giác ABC cân tại A, có $\hat{B A C} = 120 °$ và BC = 6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Các dạng bài tập Toán 9

Bài tập tìm tâm và bán kính đường tròn có đáp án chi tiết

Xem thêm các chương trình khác: