Bài tập về phương trình bậc hai một ẩn

209 lượt xem

Bài trước

Bài sau

BÀI TẬP TỔNG HỢP

A. KIẾN THỨC CẦN NHỚ

Hàm số bậc hai $y = a x^{2} (a \neq 0) :$

$a > 0$

$a < 0$

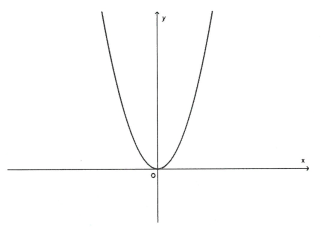
- Hàm số đồng biến khi $x > 0 .$

Hàm số nghịch biến khi $x < 0 .$

- Giá trị nhỏ nhất của hàm số là $y = 0$ khi $x = 0 .$

- Đồ thị là hàm số là một parabol nằm phía trên trục hoành và nhận trục tung làm trục đối xứng, gốc tọa độ O làm đỉnh của parabol.

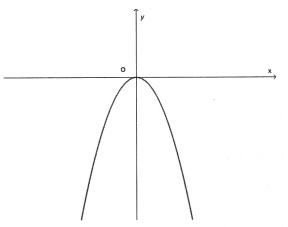
Ảnh đính kèm

- Hàm số đồng biến khi $x < 0 .$

Hàm số nghịch biến khi $x > 0 .$

- Giá trị lớn nhất của hàm số là $y = 0$ khi $x = 0 .$

- Đồ thị là hàm số là một parabol nằm phía dưới trục hoành và nhận trục tung làm trục đối xứng, gốc tọa độ O làm đỉnh của parabol.

Ảnh đính kèm

Phương trình bậc hai một ẩn: $a x^{2} + b c + c = 0 (a \neq 0) .$

$Δ = b^{2} - 4 a c$		$Δ' = b'^{2} - a c$ với $b = 2 b'$
$Δ < 0$	Phương trình vô nghiệm	$Δ' < 0$	Phương trình vô nghiệm
$Δ > 0$	Phương trình có hai nghiệm phân biệt: $x_{1} = \frac{- b + \sqrt{Δ}}{2 a}$ và $x_{2} = \frac{- b - \sqrt{Δ}}{2 a}$	$Δ' > 0$	Phương trình có hai nghiệm phân biệt: $x_{1} = \frac{- b' + \sqrt{Δ'}}{a}$ và $x_{2} = \frac{- b' - \sqrt{Δ'}}{a}$
$Δ = 0$	Phương trình có nghiệm kép: $x_{1} = x_{2} = - \frac{b}{2 a}$	$Δ' = 0$	Phương trình có nghiệm kép: $x_{1} = x_{2} = - \frac{b'}{a}$

Hệ thức Vi-et:

Nếu $x_{1}; x_{2}$ là hai nghiệm của phương trình

$a x^{2} + b c + c = 0 (a \neq 0)$ thì:

$\{\begin{cases} S = x_{1} + x_{2} = - \frac{b}{a} \\ P = x_{1} x_{2} = \frac{c}{a} \end{cases}$

Để áp dụng hệ thức Vi-et phải chú ý đến điều kiện phương trình là phương trình bậc hai có nghiệm

$\{\begin{cases} a \neq 0 \\ Δ \geq 0 \end{cases}$

Ứng dụng:

- Nhẩm nghiệm:

Trường hợp $a + b + c = 0$ thì phương trình có hai nghiệm

$x_{1} = 1$ và $x_{2} = \frac{c}{a} .$

Trường hợp $a - b + c = 0$ thì phương trình có hai nghiệm

$x_{1} = - 1$ và $x_{2} = - \frac{c}{a} .$

- Tìm hai số khi biết tổng và tích:

Nếu hai số có tổng là S là tích là P thì hai số đó là nghiệm của phương trình $x^{2} - S x + P = 0$

Điều kiện để có hai số là: $S^{2} - 4 P \geq 0 .$

- Phân tích thành nhân tử:

Nếu phương trình $a x^{2} + b c + c = 0 (a \neq 0)$ có hai nghiệm $x_{1}; x_{2}$ thì ta viết được:

$a x^{2} + b x + c = a (x - x_{1}) (x - x_{2})$

- Xét dấu của nghiệm:

P < 0	Phương trình có hai nghiệm trái dấu
P > 0 và S > 0	Phương trình có hai nghiệm dương
P > 0 và S < 0	Phương trình có hai nghiệm âm

B. BÀI TẬP TỰ LUYỆN

PHẦN I – TỰ LUẬN

Bài 1. Cho hàm số $y = (3 m^{2} + 4 m + 1) x^{2}$ . Tìm m biết:

a) Hàm số đi qua điểm $A (1; 1) .$

b) Hàm số đồng biến khi $x > 0 .$

c) Hàm số có giá trị lớn nhất bằng 0 khi x = 0.

Bài 2. Cho hàm số $y = x^{2} (P)$ và hàm số $y = 5 x - 6 (d)$ .

a) Vẽ parabol $(P)$ và đường thẳng $(d)$ trên cùng một hệ trục tọa độ Oxy.

b) Xác định tọa độ giao điểm của $(P)$ và $(d)$ .

Bài 3. Vẽ đồ thị hàm số: $y = \{\begin{cases} \frac{1}{4} x^{2}, 0 \leq x \leq 4 \\ x^{2}, - 2 \leq x \leq 0 \end{cases}$

Bài 4. Đưa các phương trình sau về dạng ${ax}^{2} + bx + c = 0$ và xác định các hệ số a, b, c.

a) $4 x^{2} - x + 1 = - 1 - 2 x$

b) $x + 3 = 1 + x - x^{2}$

c) $- 2 x^{2} - x = m$ (với m là hằng số)

d) $2 x^{2} - x = m^{2} - mx - m$ (với m là hằng số)

Bài 5. Giải phương trình bằng cách đặt nhân tử chung để đưa về phương trình tích.

a) $x^{2} - 4 x = 5$

b) $x^{2} - 5 = 0$

c) $\frac{1}{2} x^{2} - x + 1 = 0$

d) $y^{2} - 3 y = \frac{9}{4}$

Bài 6. Giải các phương trình sau:

a) $3 x^{2} - 3 x + 1 = 0$

b) $0, 7 x^{2} - x + 0, 3 = 0$

c) $\sqrt{3} x^{2} + 2 \sqrt{3} x + \sqrt{3} = 0$

d) $4 x^{2} + 2 \sqrt{3} x - 1 + \sqrt{3} = 0$

Bài 7. Giải các phương trình sau:

a) $3 x^{2} = 5 - x^{2}$

b) $(2 - \sqrt{3}) x^{2} - 3 x = 0$

c) $8 x^{2} - x + 4 = 3 (2 x + 1)$

d) $x^{4} - 3 x^{3} + x^{2} + 4 = 0$

e) $x^{4} - 2 x^{3} - 3 x^{2} + 8 x - 4 = 0$

f) ${(x^{2} - x)}^{2} = - 2 x^{3} + \sqrt{2} (x^{2} + 1)$

g) $5 + \sqrt{2 x^{2} + 3 x + 2} = (x - 1) (2 x + 5)$

h) $2 x^{4} - 21 x^{3} + 74 x^{2} - 105 x + 50 = 0$

i) $\frac{x + 2}{x - 5} + 3 = \frac{6}{2 - x}$

j) ${(2 x + 1)}^{3} + {(2 x + 5)}^{3} = 26$

k) $\frac{6 x}{4 x^{2} + 3 x - 1} + \frac{7 x}{4 x^{2} - x - 1} = 8$

Bài 8. Giải phương trình:

a) $5 {(x - 2)}^{2} + 4 = {(x + 8)}^{2}$

b) $\frac{{(x + 3)}^{2}}{5} + 1 - \frac{{(3 x - 1)}^{2}}{5} = \frac{x (2 x - 3)}{2}$

c) $\frac{1}{x^{2} - 9} + \frac{2}{x - 3} + \frac{3}{x + 3} = 1$

d) $4 - \frac{x - 1}{x + 1} = \frac{2 (x + 7)}{x - 1} - \frac{x + 11}{x^{2} - 1}$

Bài 9. Giải phương trình:

a) $x^{3} - x^{2} - 4 x + 4 = 0$

b) $2 x^{3} - 5 x^{2} + 5 x - 2 = 0$

c) $x^{3} + 8 - 4 x^{2} - 2 x = 0$

d) $x^{3} - 4 x^{2} + x + 6 = 0$

e) $x^{3} - 3 x^{2} - x + 3 = 0$

f) ${(x^{2} + 2 x - 1)}^{2} = {(x^{2} - x + 1)}^{2}$

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập về phương trình bậc hai một ẩn

Xem thêm các chương trình khác: