Bài tập về hai đường tròn cắt nhau có lời giải

202 lượt xem

Bài trước

Bài sau

BÀI TOÁN HAI ĐƯỜNG TRÒN CẮT NHAU

A. Phương pháp giải

1) Vẽ dây chung, vẽ đường nối tâm.

2) Dùng tính chất đường nối tâm là trung trực của dây chung.

B. Ví dụ minh họa

Ví dụ 1. Cho đường tròn $(O; R)$ và đường thẳng d không giao nhau. Gọi M là một điểm tùy ý trên d. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Chứng minh rằng đường thẳng AB luôn đi qua một điểm cố định.

Hướng dẫn giải

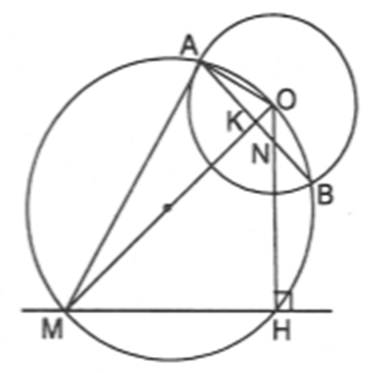
Ảnh đính kèm

Vẽ $O H ⊥ d$ . Đoạn thẳng OH cố định.

Gọi các giao điểm của AB với OH và OM lần lượt là N và K.

Ta có $A B ⊥ O M$ (tính chất dây chung); góc $\hat{O A M} = 90^{0}$ (vì điểm A nằm trên đường tròn đường kính OM).

∆OKN $~$ ∆OHM (g.g)

Suy ra $\frac{O K}{O H} = \frac{O N}{O M}$ $\Rightarrow O K . O M = O N . O H (1)$

Mặt khác:

$O K . O M = O A^{2} = R^{2} (2)$

Từ (1) và (2) suy ra $O N . O H = R^{2}$

$\Rightarrow O N = \frac{R^{2}}{O H}$ (không đổi)

Suy ra N là một điểm cố định.

Vậy AB luôn đi qua một điểm cố định là điểm N.

Ví dụ 2. Cho đường thẳng xy cắt đường tròn (O) tại hai điểm A và B (xy không đi qua O). Trên dây AB lấy một điểm M. Vẽ đường tròn (I) đi qua M và tiếp xúc với đường tròn (O) tại A. Vẽ đường tròn (K) đi qua M và tiếp xúc với đường tròn (O) tại B. Chứng minh rằng:

a) Hai đường tròn (I) và (K) cắt nhau;

b) Bán kính của đường tròn (O) bằng tổng bán kính của hai đường tròn (I) và (K).

Hướng dẫn giải

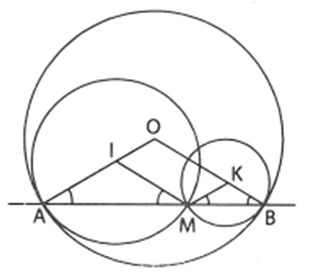
Ảnh đính kèm

a) Đường tròn (I) tiếp xúc với đường tròn (O) tại A.

Suy ra ba điểm O, I, A thẳng hàng.

Tương tự ba điểm O, K, B thẳng hàng.

Các tam giác IAM, KBM và OAB là những tam giác cân.

Suy ra:

$\hat{I A M} = \hat{I M A} = \hat{K M B} = \hat{K B M}$

Do đó $O A ∥ K M,$ $O B ∥ I M$

Vậy tứ giác OKMI là hình bình hành, dẫn tới $O I = K M,$ $O K = I M$ .

Gọi R, R₁, R₂ lần lượt là bán kính của đường tròn (O), (I) và (K).

Xét $Δ O I K$ có $|O I - O K| < I K < O I + O K$ hay $|R_{1} - R_{2}| < I K < R_{1} + R_{2}$

Do đó đường tròn (I) và (K) cắt nhau.

b) Ta có $O B = O K + K B = I M + K B$ . Suy ra $R = R_{1} + R_{2}$

Ví dụ 3. Cho hình vuông ABCD. Vẽ cung tròn $(A; A B)$ cắt nửa đường tròn (O) đường kính CD tại M. Tia CM cắt AB tại N. Chứng minh rằng N là trung điểm của AB.

Hướng dẫn giải

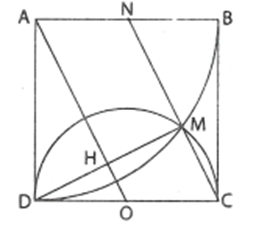
Ảnh đính kèm

Vẽ dây cung DM cắt OA tại H.

Theo tính chất dây chung ta có $H D = H M$ .

Xét $Δ M D C$ có OH là đường trung bình

Suy ra $O H ∥ C M$ $h a y O A ∥ C N$

Mặt khác, $A N ∥ O C$ nên tứ giác ANCO là hình bình hành.

Suy ra $A N = O C$ $= \frac{1}{2} C D = \frac{1}{2} A B$ .

Do đó N là trung điểm của AB.

C. Bài tập tự luyện

Bài 1. Cho hai đường tròn $(O_{1}; R_{1})$ cắt $(O_{2}; R_{2})$ tại A và B $(R_{1} > R_{2}) .$ Hãy cho biết số tiếp tuyến chung của hai đường tròn, đồng thời nêu rõ các bước vẽ các tiếp tuyến chung này.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập về hai đường tròn cắt nhau có lời giải

Xem thêm các chương trình khác: