Bài tập vị trí tương đối của hai đường tròn (Lý thuyết và bài tập)

VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

I. LÝ THUYẾT

1. Ba vị trí tương đối của hai đường tròn

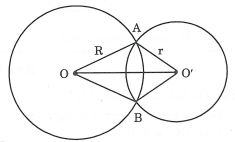
* Hai đường tròn có hai điểm chung (hình a) được gọi là hai đường tròn cắt nhau. Hai điểm chung gọi là hai giao điểm. Đoạn thẳng nối hai điểm đó gọi là dây chung.

* Hai đường tròn chỉ có một điểm chung (hình b, c) được gọi là hai đường tròn tiếp xúc nhau. Điểm chung gọi là tiếp điểm.

* Hai đường tròn không có điểm chung (hình dưới) được gọi là hai đường tròn không giao nhau.

2. Tính chất của đường tròn nối tâm – định lí

a) Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.

b) Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.

3. Các hệ thức giữa đoạn nối tâm và các bán kính

a) Hai đường tròn cắt nhau

Nếu hai đường tròn (O) và (O') cắt nhau thì

$R-r<\mathrm{OO}\text{'}<R+r$

b) Hai đường tròn tiếp xúc nhau

* Nếu hai đường tròn tiếp xúc ngoài với nhau thì: $\mathrm{OO}\text{'}=R+r$

* Nếu hai đường tròn (O) và (O') tiếp xúc trong với nhau thì:

$\mathrm{OO}\text{'}=R-r$

c) Hai đường tròn không giao nhau

Hai đường tròn ở ngoài nhau $\mathrm{OO}\text{'}>R+r$

4. Tiếp tuyến chung của hai đường tròn

Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn. Có hai loại tiếp tuyến chung là:

II. BÀI TẬP VẬN DỤNG

Bài 1. Cho ba đường tròn $\left(O;R\right)$, $\left(O\text{'};R\text{'}\right)$ và $\left(O\text{'}\text{'};R\text{'}\text{'}\right)$ đôi một tiếp xúc ngoài nhau. Tính R, R'và R'' biết $OO\text{'} = 5cm$, $OO\text{'}\text{'} = 6cm$ và $O\text{'}O\text{'}\text{'} = 7cm$

Bài 2. Cho hai đường tròn (O; 5 cm) và (O’; 5cm) cắt nhau tại A và B. Tính độ dài dây chung AB biết OO’ = 8 cm.

Bài 3. Cho hai đường tròn $\left(O;R\right)$ và $\left(O\text{'};R\text{'}\right)$ cắt nhau tại A và B với $R > R\text{'}$. Vẽ các đường kính AOC và BOD. Chứng minh rằng ba điểm B, C, D thẳng hàng

Bài 4. Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ cát tuyến chung MAN sao cho $MA = AN$. Đường vuông góc với MN tại A cắt tại I. Chứng minh I là trung điểm của $OO\text{'}$

Bài 5. Cho hai đường tròn (O) và (O') tiếp xúc ngoài nhau tại A. Gọi M là giao điểm của một trong hai tiếp tuyến chung ngoài BC $\left(B\in \left(O\right)\right), \left(C;\left(O\text{'}\right)\right)$ và tiếp tuyến chung trong tại A. Chứng minh rằng BC là tiếp tuyến của đường tròn đường kính $OO\text{'}$ tại M.

Bài 6. Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, $B\in \left(O\right), C;\left(O\text{'}\right)$. Tiếp tuyến chung ngoài, $B\in \left(O\right), C;\left(O\text{'}\right)$ . Tiếp tuyến chung trong A cắt BC tại M. Gọi E là giao điểm của OM và AB,  là giao điểm của $O\text{'}M$ và AC . Chứng minh rằng:

a) Tứ giác AEMF là hình chữ nhật

b) $OO\text{'}$là tiếp tuyến của đường tròn đường kính BC.

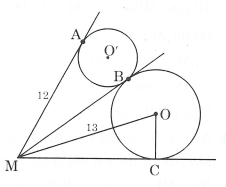
Bài 7. Ở hình dưới, đường tròn (O) và (O') tiếp xúc ngoài tại B; MB là tiếp tuyến chung trong của (O) và (O'), MA là tiếp tuyến của (O'), MC là tiếp tuyến của (O). Biết $MA = 12$, $MO = 13$. Tính bán kính của đường tròn $\left(O\right)$.

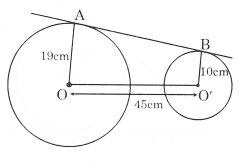
Bài 8. Ở hình dưới, AB là tiếp tuyến chung ngoài của đường tròn (O) và (O'). Biết đoạn nối tâm $OO\text{'} = 45cm$, $OA = 19cm$, $O\text{'}B = 10cm$. Tính AB

Bài 9. Cho đường tròn (O), đường kính AB. Vẽ đường tròn (O’) đường kính OA. Dây cung AC cắt đường tròn (O’) tại M. Chứng minh:

a) Đường tròn (O’) tiếp xúc với đường tròn (C) tại A.

b) O’M song song với OC.

c) OM song song với BC.

Bài 10. Cho hai đường tròn tâm O, O’ cắt nhau tại A và B (O và O’ thuộc hai nửa mặt phẳng bờ là AB). Kẻ đường kính BOC và BO’D.

a) Chứng minh ba điểm C, A, D thẳng hàng.

b) Biết OO’ =5cm, OB =4cm, O’B =3cm. Tính diện tích tam giác BCD.

Bài 11. Cho hai đường tròn (O) và (O’) cắt nhau. Tiếp tuyến chung của hai đường tròn (O) và (O’) lần lượt tại A và B. Đường thẳng AB cắt đường nối tâm OO’ tại M. Tính khoảng cách từ M đến O, O’ biết đoạn nối tâm OO’ =12cm và độ dài các bán kính của hai đường tròn (O), (O’) lần lượt là 9cm và 5cm.

Bài 12. Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài tại A. Vẽ tiếp tuyến chung ngoài BC ( BÎ (O), C Î(O’), tiếp tuyến trong tại A cắt BC tại M.

a) Chứng minh tam giác ABC và tam giác MOO’ là các tam giác vuông.

b) Tính diện tích tứ giác BCO’O, biết R= 9cm, r =4cm.

Bài 13. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Một đường thẳng kẻ qua A cắt (O) tại B, cắt (O’) tại C. Qua B và C kẻ tiếp tuyến Bx với đường tròn (O), Cy với đường tròn (O’). Chứng minh:

a) OB // O’C

b) Bx // Cy

Bài 14. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Đường nối tâm OO’ cắt đường tròn (O) ở B, cắt đường tròn (O’) tại C. Gọi DE là tiếp tuyến chung ngoài của hai đường tròn ( DÎ (O), E Î (O’)). Gọi M là giao điểm của hai đường thẳng BD và CE. Chứng minh:

a) $\widehat{DME}={90}^0$ 

b) MA là tiếp tuyến chung của hai đường tròn (O), (O’)

c) MD . MB =ME .MC

Bài 15. Cho tam giác ABC vuông tại A (AB <AC). Vẽ các đường tròn (B ; BA) và ( C; CA).

a) Chứng minh rằng hai đường tròn trên cắt nhau.

b) Vẽ bán kính CE của đường tròn ( C) vuông góc với AC.Gọi D là giao điểm thứ hai của

hai đường tròn (B) và (C). Tiếp tuyến của đường tròn (C) tại E cắt DA ở K. Chứng minh rằng: AK = BC.

Bài 16. Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC ( BÎ (O), C Î(O’).

a) Tính $\widehat{BAC}$.

b) Tính BC.

c) Gọi D là giao điểm CA với đường tròn tâm O ( D ≠ A). Chứng minh ba điểm B, O, D thẳng hàng.

Bài 17. Cho đường thẳng xy cắt đường tròn (O) tại hai điểm A và B (xy không đi qua O). Trên dây AB lấy một điểm M. Vẽ đường tròn (I) đi qua M và tiếp xúc với đường tròn (O) tại A. Vẽ đường tròn (K) đi qua M và tiếp xúc với đường tròn (O) tại B. Chứng minh rằng:

(a)    Hai đường tròn (I) và (K) cắt nhau;

(b)   Bán kính của đường tròn (O) bằng tổng bán kính của hai đường tròn (I) và (K).

Bài 18. Cho hình vuông ABCD. Vẽ cung tròn $(A;AB)$ cắt nửa đường tròn (O) đường kính CD tại M. Tia CM cắt AB tại N. Chứng minh rằng N là trung điểm của AB.

Bài 19. Cho hình bình hành ABCD, hai đường chéo cắt nhau tại M. Vẽ các đường tròn ngoại tiếp tam giác AMD và tam giác CMB. Chứng minh rằng hai đường tròn này tiếp xúc với nhau.

Bài 20. Cho góc vuông xOy. Một đường tròn có bán kính R không đổi và tâm I di động trên tia Ox sao cho $OI>R$. Vẽ đường tròn tâm K bán kính KO với K thuộc Oy sao cho hai đường tròn (I) và (K) tiếp xúc ngoài với nhau.

(a)     Gọi A là tiếp điểm của hai đường tròn. Chứng minh rằng tiếp tuyến chung của hai đường tròn tại A luôn đi qua một điểm cố định.

(b)    Đặt $OI=d$. Xác định giá trị của d để bán kính của đường tròn (K) bằng $\frac{3}{2}$ bán kính của đường tròn (I).

Bài 21. Cho đường tròn $(O;5cm)$ và đường tròn $(O\text{'};2cm);\mathrm{OO}\text{'}=9cm$. Vẽ tiếp tuyến chung ngoài tiếp xúc với đường tròn (O) tại A, tiếp xúc với đường tròn (O’) tại B. Vẽ tiếp tuyến chung trong tiếp xúc với đường tròn (O) và (O’) lần lượt tại C và D. Chứng minh rằng:

a)     Hai đường tròn (O) và (O’) không giao nhau;

b) $CD=\frac{2}{3}AB$.

Bài 22. Cho đường tròn (D) và hai điểm P, Q nằm trong đường tròn đó. Chứng minh rằng tồn tại một đường tròn nằm trong đường tròn (O) và đi qua P, Q.

Bài 23. Cho tứ giác ABCD. Vẽ đường tròn (O₁) nội tiếp tam giác ABC tiếp xúc với AC tại M. Vẽ đường tròn (O₂) nội tiếp tam giác ADC tiếp xúc với AC tại N.

a)     Chứng minh rằng $AM=\frac{AB+AC-BC}{2}$ và $AN=\frac{AD+AC-CD}{2}$

b)    Cho biết $AB+CD=AD+BC$, chứng minh rằng hai đường tròn (O₁) và (O₂) tiếp xúc ngoài với nhau.

Bài 24. Cho các đường tròn (A), (B), (C) tiếp xúc ngoài với nhau từng đôi một. Vẽ đường tròn (O) tiếp xúc trong với cả ba đường tròn (A), (B), (C). Chứng minh rằng các tam giác OAB, OBC, OCA có chu vi bằng nhau.

Bài 25. Cho hai đường tròn $(O;R)$ và $(O\text{'};R\text{'})$ tiếp xúc ngoài tại A. Trên một nửa mặt phẳng bờ OO’ vẽ các bán kính OB và O’C song song với nhau.

a)     Chứng minh rằng tam giác ABC vuông tại A.

b)    Vẽ $AH\perp BC$, tính độ dài lớn nhất của AH.

Bài 26. Cho hình vuông ABCD cạnh 11cm. Lấy tùy ý ba điểm M, N, P ở trong hình vuông. Chứng minh tồn tại một điểm nằm trên cạnh hình vuông sao cho các khoảng cách từ điểm đó đến mỗi điểm M, N, P đã cho đều lớn hơn 5cm.

Bài 27. Cho đường tròn $\left(O;R\right)$, đường kính $AB=2R$. Lấy điểm C trên đường tròn sao cho $CA<CB$. Vẽ dây CD vuông góc với AB tại H.

a)     Chứng minh rằng tam giác ABC vuông và $C{D}^2=4AH.HB$.

b)    Đường thẳng (d) tiếp xúc với đường tròn (O) tại C. Gọi M, N lần lượt là hình chiếu vuông góc của A và B trên (d). Xét vị trí tương đối của đường tròn $\left(A;AM\right)$ và đường tròn $\left(B;BN\right).$

Bài 28. Từ điểm A ngoài đường tròn $\left(O;R\right)$ sao cho $OA=2R$ vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm).

a)     Tính R theo độ dài AB.

b)    Đường cao BH của tam giác ABO kéo dài cắt đường tròn (O) tại C. Chứng minh

rằng AC là tiếp tuyến của đường tròn (O)

c)     Gọi E là giao điểm của OA với đường tròn (O) (E nằm giữa O và A). Chứng minh

rằng E là tâm đường tròn nội tiếp tam giác ABC.

Bài 29. Từ điểm M ngoài đường tròn $\left(O;R\right),$ kẻ tiếp tuyến $MA,MB$ với đường tròn (O) (A, B là hai tiếp điểm).

a)     Chứng minh rằng OM là trung trực của AB

b)    Kẻ đường kính BD của đường tròn (O). Chứng minh rằng $AD//MO.$

c)     Gọi N là giao điểm của MO với đường tròn (O) (N nằm giữa M và O). Đường thẳng BN cắt đường thẳng DA tại E. Gọi K là giao điểm của AD với DN. Chứng minh rằng $EK\perp DB$

Bài 30. Cho đường tròn $\left(O;R\right),AB$ là đường kính. Trên (O) lấy điểm C sao cho $AC=R.$

a)     Tính BC theo R

b)    Tiếp tuyến với đường tròn (O) tại C cắt đường thẳng AB tại M. Lấy trên (O) điểm D sao cho $MD=MC.$Chứng minh rằng MD là tiếp tuyến của đường tròn (O)

c)     Chứng minh rằng $M{C}^2=MA.MB$.

d)    Kẻ đường kính DE của đường tròn (O). ME cắt (O) tại F. Gọi H là giao điểm của CD với MO. Chứng minh rằng: $MF.ME=MH.MO.$

Bài 31. Cho tam giác ABC nội tiếp đường tròn $\left(O;R\right)$ có AB là đường kính $\left(AC<BC\right).$ Đường thẳng song song với AC vẽ từ O cắt đường tròn (O) tại $I(A,C,I,B$ theo thứ tự).

a)     Chứng minh rằng $OI\perp BC$.

b)    Tiếp tuyến với đường tròn (O) tại B cắt đường thẳng OI tại M. Chứng minh rằng MC là tiếp tuyến của (O)

c)     Kẻ CH vuông góc với AB tại H gọi K là giao điểm của AM với CH. Chứng minh rằng K là trung điểm của CH

Bài 32. Cho đường tròn (O) đường kính $BC=2R.$ Lấy điểm A thuộc đường tròn sao cho

$AB<AC.$ Tiếp tuyến tại A cắt tiếp tuyến tại B và C của đường tròn tại E và F

a)     Chứng minh rằng $EF=EB+FC.$

b)    Chứng minh rằng $BE.CF=R^2$.

c)     Gọi M là giao điểm của EC và BF. Kẻ đường cao AH của tam giác ABC (H thuộc BC). Chứng minh rằng ba điểm $A,M,H$ thẳng hàng.

d)    Trường hợp cho $AB=R,$chứng minh rằng tam giác AFC đều, tính theo R diện tích tam giác AFC