Bài tập tính chất của hai tiếp tuyến cắt nhau chọn lọc

253 lượt xem

TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU

I. LÝ THUYẾT

1. Định lí:

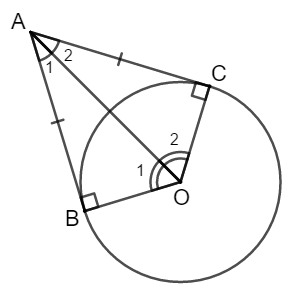Ảnh đính kèm Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm

thì:

- Điểm đó cách đều hai tiếp điểm.

- Tia từ điểm đó kẻ qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.

Ta có: $A B = A C; \hat{A_{1}} = \hat{A_{2}}; \hat{O_{1}} = \hat{O_{2}}$ .

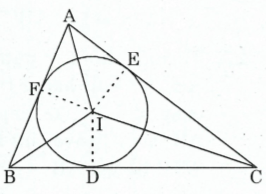2. Ảnh đính kèm Đường tròn nội tiếp tam giác:

- Đường tròn tiếp xúc với ba cạnh của tam giác là đường tròn nội tiếp tam giác.

- Tâm của đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác trong của tam giác.

3. 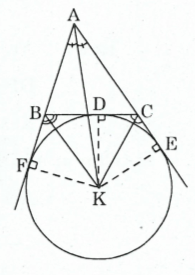Ảnh đính kèm Đường tròn bàng tiếp tam giác:

- Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh kia là đường tròn bàng tiếp của tam giác.

- Tâm của đường tròn bàng tiếp là giao điểm của hai đường phân giác ngoài của hai góc ngoài của tam giác.

- Mỗi tam giác có 3 đường tròn bàng tiếp.

II. BÀI TẬP VẬN DỤNG

Bài 1. Cho đường tròn $(O)$ , điểm nằm bên ngoài đường tròn. Kẻ các tiếp tuyến $A B, A C$ với đường tròn ( $B, C$ là các tiếp điểm).

a) Chứng minh rằng $O A$ vuông góc với $B C$ .

b) Vẽ đường kính $C D$ . Chứng minh rằng $B D$ song song với $A O$ .

c) Tính độ dài các cạnh của tam giác $A B C$ biết $O B = 2 c m, O A = 4 c m$ .

Bài 2. Từ một điểm A nằm bên ngoài đường tròn $(O)$ , kẻ các tiếp tuyến $A B, A C$ với đường tròn ( $B, C$ là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn $(O)$ nó cắt các tiếp tuyến $A B$ và $A C$ theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác $A D E$ bằng $2 A B$ .

Bài 3. Cho góc $x A y$ khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc nằm trên đường nào?

Bài 4. Cho góc $x A y$ khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn $(O)$ tiếp xúc với Ax tại B và tiếp xúc với Ay.

Bài 5. Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi $A x, B y$ là các tia vuông góc với $A B$

(Ax và By nằm cùng phía với nửa đường tròn đối với đường thẳng AB). Qua một điểm M thuộc nửa đường tròn, kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:

a) $\hat{C O D} = 90^{0}$ .

b) $C D = A C + B D$ .

c) Tích $A C . B D$ không đổi khi M điểm di chuyển trên nửa đường tròn.

Bài 6. Cho tam giác đều $A B C$ ngoại tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng:

Hãy chọn câu trả lời đúng.

Bài 7. Trên hình bên dưới, tam giác ABC ngoại tiếp đường tròn (O).

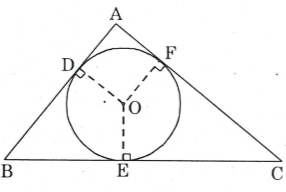
Ảnh đính kèm

a) Chứng minh rằng: $2 A D = A B + A C - B C$ .

b) Tìm các hệ thức tương tự như hệ thức ở câu a.

Bài 8. Cho đường tròn (O) đường kính AB, lấy điểm M sao cho A nằm giữa B và M. Kẻ đường thẳng MC tiếp xúc với đường tròn (O) tại C. Từ O hạ đường thẳng vuông góc với AC và cắt tia MC tại N. Chứng minh rằng đường thẳng NA là tiếp tuyến của đường tròn (O).

Bài 9. Cho $Δ A B C$ $(\hat{A} > 90^{0})$ nội tiếp đường tròn (O), kẻ đường kính BD song song với AC

a) Chứng minh đường cao BH của $Δ A B C$ là tiếp tuyến của đường tròn (O)

b) Chứng minh: $H B^{2} = H A . H C$

Bài 10. Cho $Δ A B C$ vuông tại A, đường cao AH. Đường tròn (I) đường kính BH cắt AB tại D, đường tròn (K) đường kính HC cắt AC tại E. CMR

a) AH là tiếp tuyến chung của hai đường tròn (I) và (K) tại H.

b) DE là tiếp tuyến của đường tròn (I) tại D, tiếp tuyến của đường tròn (K) tại E

Bài 11. Cho đường tròn (O; 5cm), điểm M nằm ngoài đường tròn, kẻ tiếp tuyến MA, MB (A, B là tiếp điểm). Biết $\hat{A M B} = 60^{0}$

a) Chứng minh $Δ A M B$ đều

b) Tính chu vi $Δ A M B$

c) Tia AO cắt đường tròn (O) tại C. tứ giác OCBM là hình gì? Vì sao?

Bài 12. Cho hình thang vuông ABCD ( $\hat{A} = \hat{D} = 90^{0}$ ), điểm O là trung điểm của AD và $\hat{B O C} = 90^{0}$ . Gọi E là giao điểm của BO và CD. CMR

a) Tam giác BCE can tại C

b) BC là tiếp tuyến của đường tròn đường kính AD

Bài 13. Từ một điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn. Trên tia OB lấy điểm C sao cho BC=BO. Chứng minh rằng $\hat{B M C} = \frac{1}{2} \hat{B M A}$

Bài 14. Cho đường tròn $(O; R)$ và một điểm A ở ngoài đường tròn. Vẽ các tiếp tuyến AB, AC. Chứng minh rằng $\hat{B A C} = 60^{o}$ khi và chỉ khi OA=2R

Bài 15. Từ một điểm A ở ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn. Đường thẳng vuông góc với OB tại O cắt AC tại N.Đường thằng vuông góc với OV tại O cắt AB tại M.

a) Chứng minh tứ giác AMON là hình thoi

b) Điểm A phải cách O một khoảng bao nhiêu để MN mà tiếp tuyến của (O)

Bài 16. Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Các tiếp tuyến của đường tròn vẽ từ A và C cắt nhau tại M. Trên tia AM lấy điểm D sao cho AD=BC. Chứng minh rằng:

a) Tứ giác ABCD là hình bình hành

b) Ba đường thằng AC, BD, OM đồng quy

Bài 17. Cho đường tròn (O), dây cung CD. Qua O vẽ $O H ⊥ C D$ tại H, cắt tiếp tuyến tại C của đường tròn (O) tại M. Chứng minh MD là tiếp tuyến của (O).

Bài 18. Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tia $A x ⊥ A B$ và $B y ⊥ A B$ ở cùng phía nửa đường tròn. Gọi I là một điểm trên nửa đường tròn. Tiếp tuyến tại I cắt Ax tại C và By tại D.Chứng minh $A C + B D = C D$

Bài 19. Cho đường tròn (O;5cm). Từ điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho $M A ⊥ M B$ tại M.

a) Tính MA và MB

b) Qua trung điểm I của cung nhỏ AB, vẽ một tiếp tuyến OA, OB tại C và D. Tính CD.

Bài 20. Cho đường tròn (O), Từ điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho $\hat{A M B} = 60^{o}$ .Biết chu vi tam giác MAB là 18cm. Tính độ dài dây AB

Bài 21. Cho đường tròn tâm O, bán kính $R = 6 c m$ và một điểm P cách tâm O một khoảng $O P = 10 c m$ . Từ P kẻ hai tiếp tuyến PM và PM' đến đường tròn.

1. Tính độ dài các tiếp tuyến $P M, P M'$ và dây $M M'$ .

2. Trên $O A$ , ta lấy một điểm B sao cho $A B = 8 c m$ . Tia $M B$ cắt đường tròn tại điểm C và tia $M' B$ cắt đường tròn tại điểm D.

a) Chứng minh MC là tia phân giác của góc $M' M O$ .

b) Chứng minh ba điểm $C; D; O$ thẳng hàng.

Bài 22. Cho nửa đường tròn đường kính AB, các tiếp tuyến Ax, By. Qua điểm C trên nửa đường tròn vẽ một tiếp tuyến cắt Ax, By lần lượt tại M và N. Gọi D là giao điểm của AN và BM. Đường thẳng CD cắt AB tại E. Chứng minh rằng:

a) $C D ⊥ A B$ ;

b) D là trung điểm của CE.

Bài 23. Cho đường tròn (O) và hai điểm A, B nằm ngoài đường tròn sao cho đường thẳng AB không cắt đường tròn. Vẽ các tiếp tuyến AM, BN với đường tròn (M, N là các tiếp điểm). Chứng minh rằng: $A M + B N > A B > |A M - B N|$ .

Bài 24. Cho hình vuông ABCD cạnh dài 3cm. Vẽ cung AC có tâm D bán kính 3cm. Gọi M là một điểm trên cung này. Từ M vẽ một tiếp tuyến với cung AC, cắt AB, BC lần lượt tại E và F. Chứng minh rằng: $2 c m < E F < 3 c m$

Bài 25. Từ một điểm A ở ngoài đường tròn (O; R) vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên cung nhỏ BC lấy điểm D. Tiếp tuyến của đường tròn tại D cắt AB, AC lần lượt tại M và N. Biết $\hat{B A C} = 90 °$ chứng minh rằng: $\frac{2}{3} R < M N < R$

Bài 26. Một tam giác có chu vi không đổi là 2p ngoại tiếp đường tròn (O). Vẽ một tiếp tuyến song song với một cạnh của tam giác. Tìm độ dài lớn nhất của đoạn tiếp tuyến giới hạn bởi hai cạnh kia của tam giác.

Các dạng bài tập Toán 9

Bài tập tính chất của hai tiếp tuyến cắt nhau chọn lọc

Xem thêm các chương trình khác: