Bài tập sự tương giao của hai đồ thị có lời giải chi tiết

195 lượt xem

Bài trước

Bài sau

BÀI TOÁN TƯƠNG GIAO CỦA HAI ĐỒ THỊ

A. Phương pháp giải

+) Cho đồ thị hai hàm số $(d_{1}) : y = a x + b$ và $(d_{2}) : y = a' x + b'$ .

Xét phương trình hoành độ giao điểm của $(d_{1})$ và $(d_{2})$ , ta có:

$a x + b = a' x + b'$ (1)

Khi đó hoành độ giao điểm của $(d_{1})$ và $(d_{2})$ là nghiệm của phương trình (1), sau đó thay lại vào đồ thị hàm số $(d_{1})$ hoặc $(d_{2})$ ta được tung độ của giao điểm.

+) Tọa độ giao điểm của $(d_{1}) : y = a x + b$ và trục hoành:

Ox: y = 0 $\Rightarrow 0 = a x + b \Leftrightarrow x = - \frac{b}{a}$

+) Tọa độ giao điểm của $(d_{1}) : y = a x + b$ và trục tung:

Oy: x = 0 $\Rightarrow y = a . 0 + b \Leftrightarrow y = b$

B. Ví dụ minh họa

Ví dụ 1. Cho hai hàm số $y = 3 x + 2$ có đồ thị là đường thẳng $(d_{1});$ $y = - 2 x + 7$ có đồ thị là đường thẳng $(d_{2}) .$

a) Vẽ $(d_{1})$ và $(d_{2})$ trên cùng một hệ trục tọa độ $O x y .$

b) Trên hình vẽ và bằng phép tính, hãy xác định giao điểm M của $(d_{1})$ và $(d_{2}) .$

Hướng dẫn giải

+) Xét đường thẳng $(d_{1}) : y = 3 x + 2$

Ta có bảng giá trị sau:

x	0	-1
$y = 3 x + 2$	2	-1

Trên mặt phẳng tọa độ Oxy, lấy các điểm A(0 ;2) và B(-1 ; -1). Nối các điểm A, B lại ta được đồ thị của đường thẳng $(d_{1})$ .

+) Xét đường thẳng $(d_{2}) : y = - 2 x + 7$

Ta có bảng giá trị sau:

x	0	2
$y = - 2 x + 7$	7	3

Trên mặt phẳng tọa độ Oxy, lấy các điểm C(0 ;7) và D(2 ; 3). Nối các điểm C, D lại ta được đồ thị của đường thẳng $(d_{2})$ .

+) Đồ thị hàm số

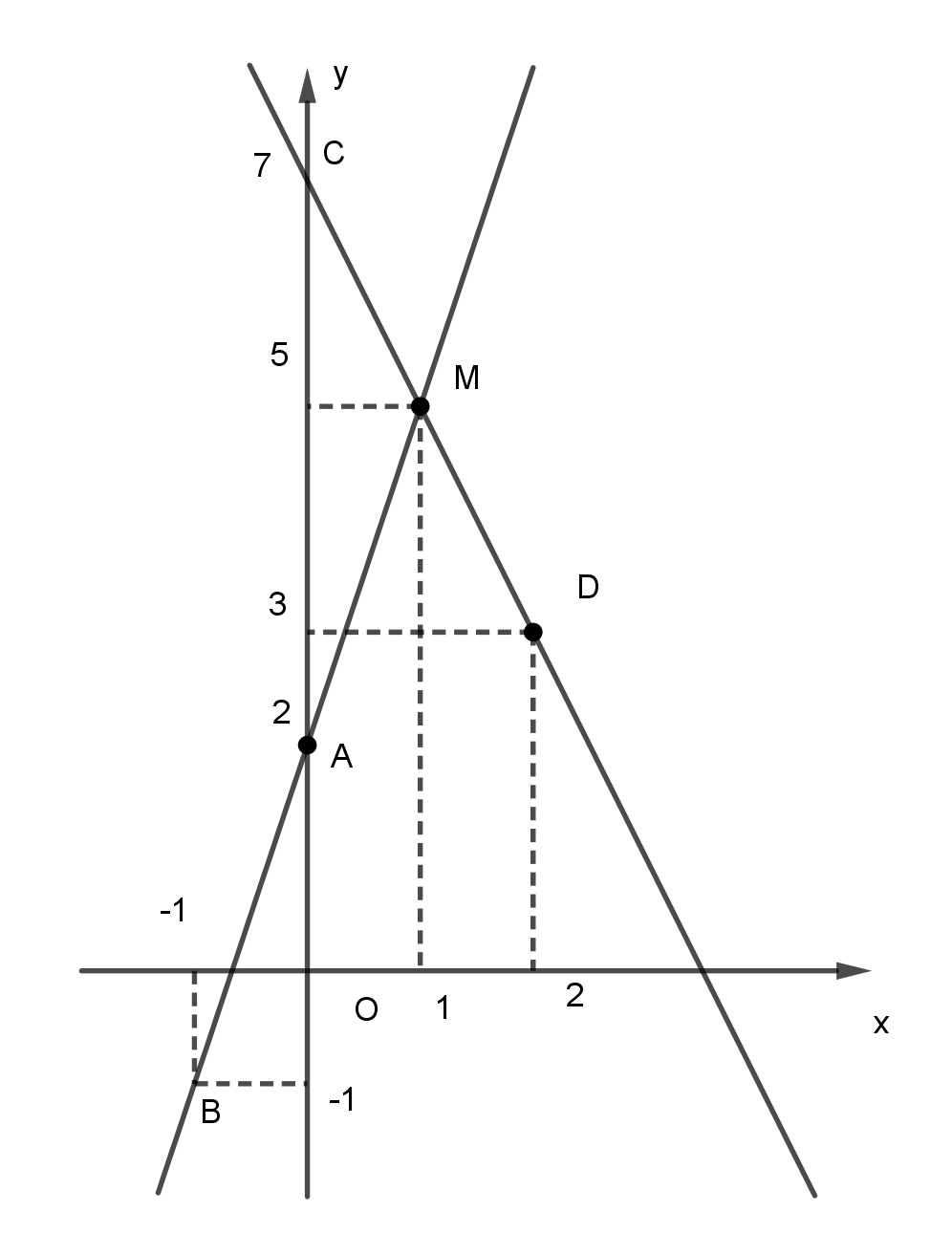
Ảnh đính kèm

b) Trên hình vẽ, có thể thấy giao điểm M của $(d_{1})$ và $(d_{2})$ có tọa độ $(1; 5) .$

Bằng phép tính: Xét phương trình hoành độ giao điểm của $(d_{1})$ và $(d_{2})$ ta được:

$3 x + 2 = - 2 x + 7$ $\Leftrightarrow 5 x = 5$ $\Leftrightarrow x = 1$ $\Rightarrow y = 5 .$ Vậy $M (1; 5) .$

Ví dụ 2. Đồ thị $(d)$ của hàm số $y = - \frac{1}{2} x + \frac{1}{5}$ cắt trục hoành tại E và cắt trục tung tại F. Tọa độ của E và F là?

Hướng dẫn giải

Điểm E thuộc trục hoành nên có tung độ bằng 0 $(y_{E} = 0) .$

Thay $(y_{E} = 0) .$ vào $y = - \frac{1}{2} x + \frac{1}{5},$ ta được:

$- \frac{1}{2} x + \frac{1}{5} = 0$ $\Leftrightarrow - 5 x_{E} + 2 = 0$ $\Leftrightarrow x_{E} = \frac{2}{5} .$

Vậy tọa độ của E là $E (\frac{2}{5}; 0) .$

Điểm F thuộc trục tung, nên có hoành độ bằng 0 $(x_{F} = 0) .$

Thay $x_{F} = 0$ vào $y = - \frac{1}{2} x + \frac{1}{5},$ ta được:

$y_{F} = - \frac{1}{2} . 0 + \frac{1}{5} \Leftrightarrow y_{F} = \frac{1}{5} .$

Vậy tọa độ của F là $F (0; \frac{1}{5}) .$

Ví dụ 3. Tìm tất cả các giá trị m để hai đường thẳng $(d_{1}) : y = m x + m + 2$ và

$(d_{2}) : y = (m + 3) x - m + 4$ cắt nhau tại điểm có tung độ bằng 2.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập sự tương giao của hai đồ thị có lời giải chi tiết

Xem thêm các chương trình khác: