Cách xét tính đồng biến, nghịch biến của hàm số cực hay, chi tiết

190 lượt xem

Bài trước

Bài sau

THẾ NÀO LÀ MỘT HÀM SỐ BẬC NHÂT, XÉT TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ BẬC NHẤT

A. Phương pháp giải

* Hàm số y = ax+b là hàm số bậc nhất nếu $a \neq 0$

* Xét tính đồng biến, nghịch biến của hàm số

+ Hàm số y = f(x) đồng biến nếu với mọi x₁; x₂ thuộc tập xác định thỏa mãn x₁ < x₂ thì f(x₁) < f(x₂)

+ Hàm số y = f(x) nghịch biến nếu với mọi x₁; x₂ thuộc tập xác định thỏa mãn x₁ < x₂ thì f(x₁) > f(x₂)

+ Ngoài dựa vào định nghĩa, ta có thể dựa vào việc xét dấu biểu thức

A = (f(x₁)- f(x₂))(x₁ - x₂) hoặc $B = \frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}}$ .

Nếu A > 0 (hoặc B > 0 ) thì hàm số đồng biến.

Nếu A < 0 (hoặc B < 0) thì hàm số nghịch biến.

B. Ví dụ minh họa

Ví dụ 1: Xét tính đồng biến, nghịch biến của các hàm số:

a) y = f(x) = 3x-7 .

b) y = g(x) = -2x+5 .

c) y = h(x) = √(x+2)

Hướng dẫn giải:

a) Lấy x₁ ≠ x₂ ∈ R, ta có:

$\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}}$ $= \frac{(3 x_{1} - 7) - (3 x_{2} - 7)}{x_{1} - x_{2}}$ $= \frac{3 (x_{1} - x_{2})}{x_{1} - x_{2}} = 3 > 0$

Vậy hàm số đồng biến trên toàn tập số thực.

b) Lấy x₁ ≠ x₂ ∈ R, ta có:

$\frac{g (x_{1}) - g (x_{2})}{x_{1} - x_{2}}$ $= \frac{(- 2 x_{1} + 5) - (- 2 x_{2} + 5)}{x_{1} - x_{2}}$ $= \frac{2 x_{2} - 2 x_{1}}{x_{1} - x_{2}}$ $= - 2 < 0$

Vậy hàm số y = g(x) nghịch biến trên toàn tập số thực.

c) Đkxđ : x ≥ -2.

Lấy x₁ ≠ x₂ thỏa mãn x₁; x₂ ≥ -2 ta có:

$\begin{array}{l} \frac{h (x_{1}) - h (x_{2})}{x_{1} - x_{2}} = \frac{\sqrt{x_{1} + 2} - \sqrt{x_{2} + 2}}{x_{1} - x_{2}} \\ = \frac{(x_{1} + 2) - (x_{2} + 2)}{(\sqrt{x_{1} + 2} + \sqrt{x_{2} + 2}) (x_{1} - x_{2})} \\ = \frac{x_{1} - x_{2}}{(\sqrt{x_{1} + 2} + \sqrt{x_{2} + 2}) (x_{1} - x_{2})} \\ = \frac{1}{\sqrt{x_{1} + 2} + \sqrt{x_{2} + 2}} > 0 \end{array}$

Vậy hàm số đồng biến trên tập xác định x ≥ -2.

Ví dụ 2: Với những giá trị nào của m thì hàm số sau là hàm số bậc nhất?

a, y= mx - 2(x-m)

$b, y = (\frac{2}{\sqrt{m - 2}} - 1) x - 2$

$c, y = \frac{m - 1}{m^{2} - 1} (x + 2)$

d, y= (m² - 3m + 2)x² + 2(m-2)(m+1)x - 3m - 2.

Hướng dẫn giải

a) Hàm số y = mx - 2(x-m) = (m-2)x + 2m có hệ số a=m-2.

Vậy hàm số y = mx - 2(x-m) là hàm số bậc nhất ⇔ a ≠ 0 ⇔ m - 2 ≠ 0 ⇔ m ≠ 2.

b) Hàm só $y = (\frac{2}{\sqrt{m - 2}} - 1) x - 2$ có hệ só $a = (\frac{2}{\sqrt{m - 2}} - 1)$

Hàm số là hàm số bậc nhất $\Leftrightarrow a \neq 0$

$\frac{2}{\sqrt{m - 2}} - 1 \neq 0$ $\Leftrightarrow \{\begin{cases} m - 2 > 0 \\ \frac{2}{\sqrt{m - 2}} \neq 1 \end{cases}$ $\Leftrightarrow \{\begin{cases} m > 2 \\ \sqrt{m - 2} \neq 2 \end{cases}$

Vậy m > 2 và m ≠ 6.

c) $y = \frac{m - 1}{m^{2} - 1} (x + 2)$ $= \frac{m - 1}{m^{2} - 1} x + 2 \cdot \frac{m - 1}{m^{2} - 1}$ là hàm số bậc nhất

$\Leftrightarrow a \neq 0$ $\Leftrightarrow \frac{m - 1}{m^{2} - 1} \neq 0$ $\Leftrightarrow m \neq \pm 1$

Vậy m ≠ ± 1

d) $y = (m^{2} - 3 m + 2) x^{2}$ $+ 2 (m - 2) (m + 1) x - 3 m - 2$ là hàm số bậc nhất

$\Leftrightarrow \{\begin{cases} m^{2} - 3 m + 2 = 0 \\ 2 (m - 2) (m + 1) \neq 0 \end{cases}$ $\Leftrightarrow \{\begin{cases} (m - 1) (m - 2) = 0 \\ (m - 2) (m + 1) \neq 0 \end{cases}$

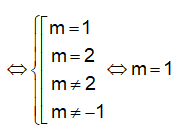
Ảnh đính kèm

Vậy m = 1

Ví dụ 3: Cho hàm số $y = (3 - \sqrt{m + 2}) x$ . Với gía trị nào của m thì :

a, Hàm số đã cho là hàm bậc nhất

b, Hàm số đã cho đồng biến

c, Hàm số đã cho nghịch biến

Hướng dẫn giải

Hàm số đã cho có hệ số a = $3 - \sqrt{m + 2}$

a, Hàm số đã cho là hàm bậc nhất ⇔ a ≠ 0

$\Leftrightarrow 3 - \sqrt{m + 2} \neq 0$ $\Leftrightarrow \sqrt{m + 2} \neq 3$ $\Leftrightarrow m + 2 \neq 9 \Leftrightarrow m \neq 7$

Vậy m ≠ 7

b, Hàm số đã cho đồng biến khi a > 0

$\Leftrightarrow 3 - \sqrt{m + 2} > 0$ $\Leftrightarrow \sqrt{m + 2} < 3$ $\Leftrightarrow 0 \leq m + 2 < 9$ $\Leftrightarrow - 2 \leq m < 7$

Vậy -2 ≤ m < 7

c, Hàm số đã cho nghịch biến khi a < 0

$\Leftrightarrow 3 - \sqrt{m + 2} < 0$ $\Leftrightarrow \sqrt{m + 2} > 3$ $\Leftrightarrow m + 2 > 9$ $\Leftrightarrow m > 7$

Vậy m > 7.

C. Bài tập tự luyện

Bài 1: Cho hàm số $y = (2 m + 1) x + 3$ .

1) Xác định m để hàm số đồng biến trên R.

2) Tìm tất cả các giá trị của m để hàm số nghịch biến trên R.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Cách xét tính đồng biến, nghịch biến của hàm số cực hay, chi tiết

Xem thêm các chương trình khác: