Bài tập tính diện tích tam giác, tứ giá bằng tỉ số lượng giác chọn lọc

204 lượt xem

Bài trước

Bài sau

TÍNH DIỆN TÍCH TAM GIÁC, DIỆN TÍCH TỨ GIÁC NHỜ SỬ DỤNG CÁC TỈ SỐ LƯỢNG GIÁC

A. Một số ví dụ

Ví dụ 1. Chứng minh rằng diện tích một tam giác bằng nửa tích hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.

Giải

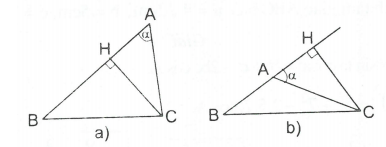
Gọi $α$ là góc nhọn tạo bởi hai đường thẳng chứa hai cạnh AB, AC của tam giác ABC. Vẽ đường cao CH. Xét $Δ A C H$ vuông tại H có $C H = A C . \sin α$

Diện tích $Δ A B C$ là $S = \frac{1}{2} A B . C H .$ Do dó $S = \frac{1}{2} A B . A C . \sin α .$

Ví dụ 2. Tứ giác ABCD có $A C = m, B D = n,$ góc nhọn tạo bởi hai đường chéo bằng $α$ .

Chứng minh rằng diện tích của tứ giác này được tính theo công thức $S = \frac{1}{2} m n \sin α .$

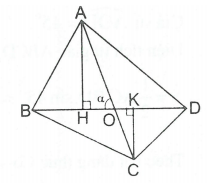Ảnh đính kèm Giải

Gọi O là giao điểm của AC và BD. Giả sử $\hat{B O C} = α .$

Vẽ $A H ⊥ B D, C K ⊥ B D .$

Ta có $A H = O A \sin α;$

$C K = O C \sin α$ và $O A + O C = A C .$

Diện tích tứ giác ABCD là:

$\begin{array}{l} S = S_{A B D} + S_{C B D} \\ = \frac{1}{2} B D . A H + \frac{1}{2} B D . C K \\ = \frac{1}{2} B D (A H + C K) \\ = \frac{1}{2} B D (O A s i n α + O C \sin α) \\ = \frac{1}{2} B D \sin α (O A + O C) \\ = \frac{1}{2} A C . B D \sin α = \frac{1}{2} m n \sin α \end{array}$

Ví dụ 3. Cho tam giác nhọn ABC. Gọi độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Tính diện tích tam giác ABC biết

$a = 4 \sqrt{2} c m, b = 5 c m, c = 7 c m .$

Giải

Theo định lí côsin ta có:

$a^{2} = b^{2} + c^{2} - 2 b c \cos A .$

Do đó

${(4 \sqrt{2})}^{2} = 5^{2} + 7^{2} - 2.5.7 . \cos A$

Suy ra $\cos A = \frac{3}{5}$ $\Rightarrow \sin A = \sqrt{1 - \cos^{2} A}$ $= \sqrt{1 - \frac{9}{25}} = \frac{4}{5}$

Vậy diện tích tam giác ABC là:

$S = \frac{1}{2} b c \sin A$ $= \frac{1}{2} . 5.7 . \frac{4}{5} = 14 (c m^{2})$

Ví dụ 4. Tứ giác ABCD có $A C + B D = 12 c m .$ Góc nhọn giữa hai đường chéo là $45 ° .$ Tính diện tích lớn nhất của tứ giác đó.

Giải

Gọi O là giao điểm của AC và BD.

Giả sử $\hat{A O D} = 45 ° .$

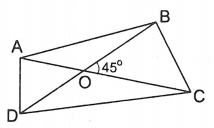
Ảnh đính kèm

Diện tích tứ giác ABCD là:

$S = \frac{1}{2} A C . B D . \sin 45 °$ $= \frac{1}{2} A C . B D . \frac{\sqrt{2}}{2}$ $= \frac{\sqrt{2}}{4} . A C . B D$

Theo bất đẳng thức Cô-si, ta có:

$A C . B D \leq {(\frac{A C + B D}{2})}^{2}$

Do đó $S \leq \frac{\sqrt{2}}{4} {(\frac{A C + B D}{2})}^{2}$ $= \frac{\sqrt{2}}{4} . 6^{2} = 9 \sqrt{2} (c m^{2})$

Vậy $\max S = 9 \sqrt{2} c m^{2}$ khi $A C = B D = 6 c m .$

Ví dụ 5. Cho tam giác $A B C, \hat{A} = 60 ° .$ Vẽ đường phân giác AD.

Chứng minh rằng: $\frac{1}{A B} + \frac{1}{A C} = \frac{\sqrt{3}}{A D}$

Giải

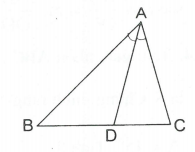
Ảnh đính kèm

Ta có

$S_{A B D} = \frac{1}{2} A B . A D . \sin 30 °$ $= \frac{1}{2} A B . A D . \frac{1}{2}$

$S_{A C D} = \frac{1}{2} A C . A D . \sin 30 °$ $= \frac{1}{2} A C . A D . \frac{1}{2} .$

$S_{A B C} = \frac{1}{2} A B . A C . \sin 60 °$ $= \frac{1}{2} A B . A C . \frac{\sqrt{3}}{2}$

Mặt khác $S_{A B D} + S_{A C D} = S_{A B C}$ nên $\frac{1}{2} A B . A D . \frac{1}{2} + \frac{1}{2} A C . A D . \frac{1}{2}$ $= \frac{1}{2} A B . A C . \frac{\sqrt{3}}{2}$

Do đó $A D (A B + A C) = A B . A C \sqrt{3}$

Suy ra $\frac{A B + A C}{A B . A C} = \frac{\sqrt{3}}{A D}$ $h a y \frac{1}{A B} + \frac{1}{A C} = \frac{\sqrt{3}}{A D} .$

Ví dụ 6. Tam giác ABC có mỗi cạnh đều nhỏ hơn 4cm. Chứng minh rằng tam giác này có diện tích nhỏ hơn $7 c m^{2}$ .

Giải

Giả sử $\hat{A} \leq \hat{B} \leq \hat{C},$ khi đó $\hat{A} \leq 60 °$ và $\sin A \leq \frac{\sqrt{3}}{2}$

Diện tích tam giác ABC là:

$S = \frac{1}{2} A B . A C . \sin A \leq \frac{1}{2} . 4.4 . \frac{\sqrt{3}}{2}$ $= 4 \sqrt{3} = 6, 92 . . . < 7 (c m^{2}) .$

B. Bài tập vận dụng

5.1. Chứng minh rằng diện tích cùa hình bình hành bằng diện tích của hai cạnh kề nhân với sin của góc nhọn tạo bởi hai đường thẳng chứa hai cạnh ấy.

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập tính diện tích tam giác, tứ giá bằng tỉ số lượng giác chọn lọc

Xem thêm các chương trình khác: