TỨ GIÁC NỘI TIẾP VÀ CÁC BÀI TOÁN LIÊN QUAN ĐẾN TỨ GIÁC NỘI TIẾP
A. Phương pháp giải
Đối với chứng minh tứ giác nội tiếp, ta sử dụng các dấu hiệu nhận biết sau:
+ Tứ giác có tổng hai góc đối bằng 180°.
+ Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
+ Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.
+ Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
+ Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.
Đối với bài toán tính góc, ta sử dụng các tính chất của tứ giác nội tiếp để tính toán.
B. Ví dụ minh họa
Ví dụ 1: Tính số đo các góc của tứ giác ABCD
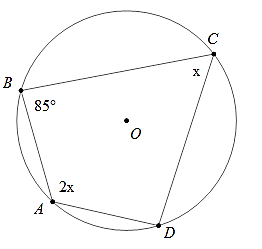
Hướng dẫn giải:
Do ABCD là tứ giác nội tiếp nên
Vì nên
Ta có:
Vậy .
Ví dụ 2: Cho đường tròn tâm O. Từ điểm A ở bên ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC với đường tròn (B, C là hai tiếp điểm). Trên BC lấy điểm M, vẽ đường thẳng vuông góc với OM tại M, cắt AB và AC lần lượt tại E và D. Chứng minh các tứ giác EBOM và DCMO nội tiếp được trong đường tròn. Xác định tâm các đường tròn đó.
Hướng dẫn giải

– Chứng minh tứ giác EBOM nội tiếp
Có OM ⊥ ME (gt) nên góc
OB ⊥ BE (BE là tiếp tuyến của (O)) nên góc
Tứ giác EBOM nội tiếp trong đường tròn đường kính OE.
– Chứng minh tứ giác DCMO nội tiếp
Có OMDM (gt) nên góc
CD ⊥ OC (CĐ là tiếp tuyến của (O)) nên góc
Nên M, C là hai đỉnh liên tiếp cùng nhìn OD dưới một góc
Tứ giác DCMO nội tiếp trong đường tròn đường kính OD.
Ví dụ 3: Qua điểm B nằm ở bên ngoài đường tròn (O), vẽ hai tiếp tuyến BC và BD với đường tròn (O), (C, D là các tiếp điểm). Từ B vẽ cát tuyến BMN (M nằm giữa B và N, tia BN nằm giữa hai tia BC và BO), gọi H là giao điểm của BO và CD.
a. Chứng minh BM.BN = BH.BO.
b. Chứng minh tứ giác OHMN nội tiếp.
Hướng dẫn giải

a. Ta có: BC = BD (tính chất hai tiếp tuyến cắt nhau)
OC = OD (bán kính đường tròn (O))
BO là đường trung trực của CD BO ⊥ CD (1)
Xét △BMC và △BCN có:
: chung
(cùng chắn cung )
(g – g)
(2)
Do (1) ta có △BCO vuông tại C, đường cao CH:
(hệ thức lượng trong tam giác vuông) (3)
Từ (2) và (3) BM.BN = BH.BO.
b. Ta có: BM.BN = BH.BO (chứng minh trên)
△BMO và △BHN có:
: chung
(c – g – c)
(hai góc tương ứng)
Tứ giác OHMN nội tiếp (hai góc bằng nhau cùng nhìn một cạnh).
C. Bài tập tự luyện
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) với trực tâm là H. Giả sử M là một điểm trên cung BC không chứa A (M khác B, M khác C). Gọi N, P theo thứ tự là điểm đối xứng của M qua các đường thẳng AB, AC.
a) Chứng minh tứ giác AHCP nội tiếp.
b) Chứng minh ba điểm N, H, P thẳng hàng.
c) Tìm vị trí của M để độ dài đoạn NP lớn nhất.
Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

