ÔN TẬP: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
A – LÝ THUYẾT
I . Hệ thức lượng về cạnh và đường cao trong tam giác vuông:
1. Cho tam giác ABC vuông tại A, đường cao AH. Ta có:
(1) b2 = ab’; c2 = ac’.
(2) b2 + c2 = a2 (định lý Pitago)
(3) h2 = b’c’
(4) ah = bc
(5)
2. Các hệ thức (1), (3), (4) và (5) ở trên có định lý đảo với điều kiện H nằm giữa B và C.
3. Đối với DABC bất kỳ, ta có:
(định lý Py-ta-go);
II . Tỉ số lượng giác của góc nhọn:

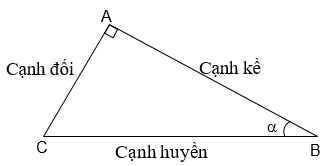
· Nếu hai góc nhọn a và b có sina = sinb (hoặc cosa = cosb, hoặc tana = tanb, hoặc cota = cotb) thì a = b.
· Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia và tan góc này bằng cot góc kia.
Nếu a + b = 900 thì:
sina = cosb; cosa = sinb;
tana = cotb; cota = tanb.
II . Hệ thức lượng giữa các cạnh và các góc của một tam giác vuông:
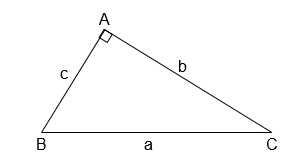
b = a.sinB = a.cosC
c = a.sinC = a.cosB
b = c.tanB = c.cotC
c = b.tanC = b.cotB
B – CÁC VÍ DỤ.
DẠNG 1: Vận dụng hệ thức về cạnh và đường cao để tính cạnh trong tam giác.
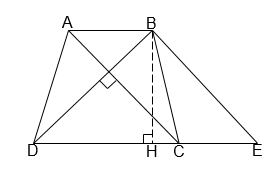
Ví dụ 1: Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
Giải:
|
Qua B vẽ đường thẳng song song với AC, cắt DC ở E. Gọi BH là đường cao của hình thang. Ta có BE // AC, AC ^ BD nên BE ^ BD. Áp dụng định lý Pitago vào tam giác vuông BDH, ta có: BH2 + HD2 = BD2 |
|
122 + HD2 = 152 Þ HD2 = 225 – 144 = 81 Þ HD = 9 (cm).
Xét tam giác BDE vuông tại B:
BD2=DE.DHÞ152=DE.9ÞDE=225:9=25 (cm).
Ta có: AB=CE nên AB+CD=CE+CD=DE=25 (cm).
Do đó: = 25 . 12 : 2 = 150 (cm2).
Ví dụ 2: Hình thang cân ABCD có đáy lớn CD = 10cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính đường cao của hình thang.
Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.