Bài tập vị trí tương đối của hai đường tròn có đáp án

205 lượt xem

Bài trước

Bài sau

VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

A. Phương pháp giải

+) Hai đường tròn có thể:

- Không cắt nhau:

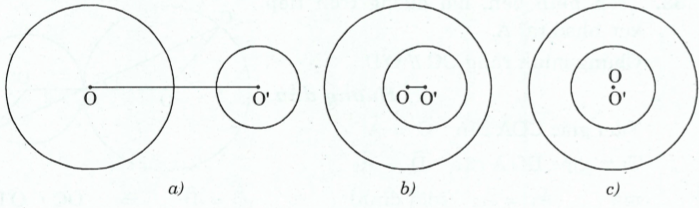
Ảnh đính kèm

- Tiếp xúc với nhau:

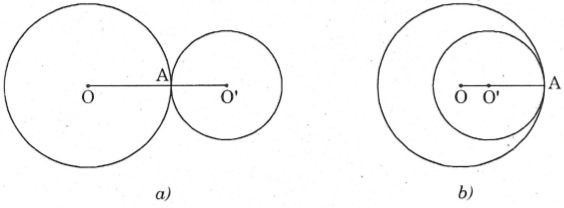
Ảnh đính kèm

- Cắt nhau tại 2 giao điểm:

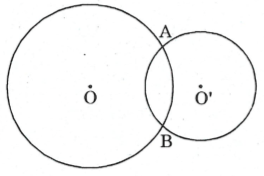
Ảnh đính kèm

+) Hệ thức giữa đoạn nối tâm và các bán kính:

Gọi d là đoạn nối tâm: $O O' = d$ ;

$R, r$ là các bán kính của hai đường tròn.

Ta có:

$R - r < d < R + r$ : Hai đường tròn cắt nhau.

$d = R + r$ : Hai đường tròn tiếp xúc ngoài.

$d = R - r > 0$ : Hai đường tròn tiếp xúc trong.

$d > R + r$ : Hai đường tròn ngoài nhau (không cắt nhau).

$d > R - r$ : Hai đường tròn đựng nhau.

Đặc biệt: $d = 0$ : Hai đường tròn đồng tâm.

B. Ví dụ minh họa

Ví dụ 1. Trên hình bên, hai đường tròn tiếp xúc nhau tại A.

Chứng minh rằng $O C / / O' D$ .

Hướng dẫn giải

Tam giác $C O A$ cân: $\hat{C} = \hat{A_{1}}$ .

Tam giác $D O' A$ cân: $\hat{D} = \hat{A_{2}}$ .

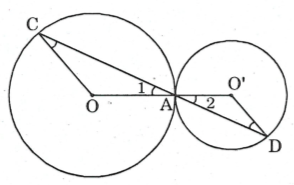
Mà $\hat{A_{1}} = \hat{A_{2}}$ (đối đỉnh) $\Rightarrow \hat{C} = \hat{D}$ $\Rightarrow O C / / O' D$ .

Ví dụ 2. Cho hai đường tròn $(O; 20 c m)$ và $(O'; 15 c m)$ cắt nhau tại A và B. Tính đoạn nối tâm $O O'$ biết rằng $A B = 24 c m$ (xét hai trường hợp $O$ và $O'$ khác phía đối với $A B$ , $O$ và $O'$ cùng phía đối với $A B$ ).

Hướng dẫn giải

a) Trường hợp $O$ và $O'$ khác phía đối với $A B$ .

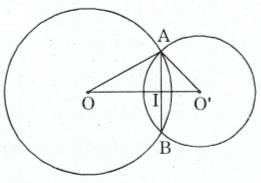
Ảnh đính kèm

Ta có:

$\begin{array}{l} A I = \frac{1}{2} A B = 12 \\ O I^{2} = O A^{2} - A I^{2} \\ \Rightarrow O I = \sqrt{56} \\ O' I^{2} = O' A^{2} - A I^{2} \\ \Rightarrow O' I = 9 \\ \Rightarrow O O' = 9 + \sqrt{56} \approx 16, 5 \end{array}$

b) Trường hợp $O$ và $O'$ cùng phía đối với $A B$ .

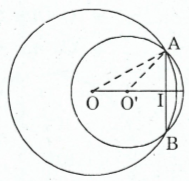
Ảnh đính kèm

Ta có:

$O I^{2} = O A^{2} - A I^{2}$ $\Rightarrow O I = \sqrt{56}$ .

Tương tự: $O' I = 9$ .

Do đó:

$O O' = O I - O' I$ $= 9 - \sqrt{56} \approx 1, 5$ .

Ví dụ 3. Cho đường tròn $(O)$ có bán kính $O A$ và đường tròn đường kính $O A$ .

a) Hãy xác định vị trí của hai đường tròn.

b) Dây $A D$ của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng: $A C = C D$ .

Hướng dẫn giải

Ảnh đính kèm

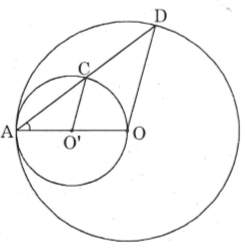
Ta có:

$\begin{array}{l} O A = R \\ r = O' A = \frac{R}{2} \\ O O' = \frac{R}{2} \end{array}$

Từ $O O' = O A - O' A$ $\Rightarrow O O' = R - r$ .

Vậy hai đường tròn tiếp xúc trong.

b) Tam giác $A O D$ cân $\Rightarrow \hat{D} = \hat{A}$ .

Tam giác $A O' C$ cân $\Rightarrow \hat{C} = \hat{A}$ .

$\Rightarrow \hat{D} = \hat{C}$ $\Rightarrow O' C / / O D$ .

$O'$ là trung điểm của $O A$ , suy ra $C$ là trung điểm của $A D$ .

$\Rightarrow A C = C D$ .

C. Bài tập tự luyện

Bài 1. Cho đường tròn (O) bán kính OA và đường tròn đường kính OA.

a) Hãy xác định vị trí của hai đường tròn (O) và đường tròn đường kính OA.

b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng $A C = C D .$

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Các dạng bài tập Toán 9

Bài tập vị trí tương đối của hai đường tròn có đáp án

Xem thêm các chương trình khác: