Giá trị của $x$ thỏa mãn \({\log _{\frac{1}{2}}}(3 - x) = 2\) là
Phương trình tương đương với:
\(3 - x = {\left( {\dfrac{1}{2}} \right)^2} \Leftrightarrow x = \dfrac{{11}}{4}\)
Vậy $x = \dfrac{{11}}{4}$.
Nghiệm của phương trình \({\log _2}(x + 4) = 3\) là:
Điều kiện: \(x + 4 > 0 \Leftrightarrow x > - 4\).
\({\log _2}(x + 4) = 3 \Leftrightarrow x + 4 = {2^3} \Leftrightarrow x = 4\)
Vậy phương trình đã cho có một nghiệm \(x = 4\).
Đề thi THPT QG - 2021 - mã 103
Nghiệm của phương trình \({\log _3}\left( {2x} \right) = 2\) là:
\({\log _3}\left( {2x} \right) = 2 \Leftrightarrow 2x = 9 \Leftrightarrow x = \dfrac{9}{2}\).
Cho $a, b, c$ là ba số thực dương, \(a > 1\) thỏa mãn
\(\log _a^2(bc) + {\log _a}{\left( {{b^3}{c^3} + \dfrac{{bc}}{4}} \right)^2}\)\( + 4 + \sqrt {9 - {c^2}} = 0\)
Khi đó, giá trị của biểu thức \(T = a + 3b + 2c\) gần với giá nào nhất sau đây?
Áp dụng bất đẳng thức \({(x + y)^2} \ge 4xy\), ta được
\({\left( {{b^3}{c^3} + \dfrac{{bc}}{4}} \right)^2} \ge {b^4}{c^4}\)
\( \Rightarrow {\log _a}{\left( {{b^3}{c^3} + \dfrac{{bc}}{4}} \right)^2}\)\( \ge 4{\log _a}(bc)\)
Do đó với \(\forall a > 1,b,c > 0\)
\(\log _a^2(bc) + {\log _a}{\left( {{b^3}{c^3} + \dfrac{{bc}}{4}} \right)^2}\)\( + 4 + \sqrt {9 - {c^2}} \ge \log _a^2(bc)\)\( + 4{\log _a}(bc) + 4 + \sqrt {9 - {c^2}} \)
\( \Leftrightarrow \log _a^2(bc) + {\log _a}{\left( {{b^3}{c^3} + \dfrac{{bc}}{4}} \right)^2}\)\( + 4 + \sqrt {9 - {c^2}} \)\( \ge {\left[ {{{\log }_a}(bc) + 2} \right]^2} + \sqrt {9 - {c^2}} \ge 0\)
Dấu "=" xảy ra khi \(\left\{ \begin{array}{l}{b^3}{c^3} = \dfrac{{bc}}{4}\\{\log _a}\left( {bc} \right) = - 2\\{c^2} = 9\\a > 1\\b > 0\\c > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \sqrt 2 \\b = \dfrac{1}{6}\\c = 3\end{array} \right.\)
Khi đó \(T = a + 3b + 2c\)\( = \sqrt 2 + \dfrac{1}{2} + 6 \approx 7,91\)
Vậy giá trị của T gần 8 nhất.
Nghiệm của phương trình \({\log _2}\left( {3x} \right) = 3\) là:
ĐKXĐ: \(x > 0\).
Ta có: \({\log _2}\left( {3x} \right) = 3 \Leftrightarrow 3x = {2^3} \)\(\Leftrightarrow 3x = 8 \Leftrightarrow x = \dfrac{8}{3}\)
Vậy phương trình có nghiệm \(x = \dfrac{8}{3}\).
Đề thi THPT QG 2019 – mã đề 104
Nghiệm của phương trình \({\log _3}\left( {2x + 1} \right) = 1 + {\log _3}\left( {x - 1} \right)\) là
\(\begin{array}{l}\,\,\,\,\,\,\,{\log _3}\left( {2x + 1} \right) = 1 + {\log _3}\left( {x - 1} \right)\\ \Leftrightarrow {\log _3}\left( {2x + 1} \right) = {\log _3}3 + {\log _3}\left( {x - 1} \right)\\ \Leftrightarrow {\log _3}\left( {2x + 1} \right) = {\log _3}\left[ {3\left( {x - 1} \right)} \right]\\ \Leftrightarrow \left\{ \begin{array}{l}2x + 1 = 3x - 3\\3x - 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\x > 1\end{array} \right. \Leftrightarrow x = 4\end{array}\)
Vậy nghiệm của phương trình là \(x = 4\).
Đề thi THPT QG 2019 – mã đề 104
Cho phương trình \({\log _9}{x^2} - {\log _3}\left( {4x - 1} \right) = - {\log _3}m\) (\(m\) là tham số thực). Có tất cả bao nhiêu giá trị nguyên của \(m\) để phương trình đã cho có nghiệm?
ĐK: \(\left\{ \begin{array}{l}{x^2} > 0\\4x - 1 > 0\\m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x > \dfrac{1}{4}\\m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > \dfrac{1}{4}\\m > 0\end{array} \right.\)
\(\begin{array}{l}{\log _9}{x^2} - {\log _3}\left( {4x - 1} \right) = - {\log _3}m\\ \Leftrightarrow {\log _3}x - {\log _3}\left( {4x - 1} \right) + {\log _3}m = 0\\ \Leftrightarrow {\log _3}\dfrac{{mx}}{{4x - 1}} = 0 \Leftrightarrow \dfrac{{mx}}{{4x - 1}} = 1\\ \Leftrightarrow mx = 4x - 1\,\,\left( {Do\,\,4x - 1 > 0} \right)\\ \Leftrightarrow m = \dfrac{{4x - 1}}{x} = g\left( x \right)\,\,\forall x > \dfrac{1}{4}\,\,\left( * \right)\end{array}\)
Số nghiệm của phương trình là số giao điểm trên \(\left( {\dfrac{1}{4}; + \infty } \right)\) của đồ thị hàm số \(y = g\left( x \right)\) và đường thẳng \(y = m\) song song với trục hoành.
Xét hàm số \(g\left( x \right) = \dfrac{{4x - 1}}{x} = 4 - \dfrac{1}{x}\) trên \(\left( {\dfrac{1}{4}; + \infty } \right)\) ta có \(g'\left( x \right) = \dfrac{1}{{{x^2}}} > 0\,\,\forall x \in \left( {\dfrac{1}{4}; + \infty } \right)\).
BBT:
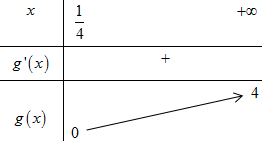
Từ BBT ta thấy (*) có nghiệm \( \Leftrightarrow m \in \left( {0;4} \right)\,\,\left( {tm\,\,DK\,\,m > 0} \right)\).
Kết hợp điều kiện \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2;3} \right\}\). Vậy có 3 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Cho phương trình \(m{\ln ^2}\left( {x + 1} \right) - \left( {x + 2 - m} \right)\ln \left( {x + 1} \right) - x - 2 = 0\) \(\left( 1 \right)\). Tập tất cả giá trị của tham số \(m\) để phương trình \(\left( 1 \right)\) có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn \(0 < {x_1} < 2 < 4 < {x_2}\) là khoảng \(\left( {a; + \infty } \right)\). Khi đó, \(a\) thuộc khoảng
\(m{\ln ^2}\left( {x + 1} \right) - \left( {x + 2 - m} \right)\ln \left( {x + 1} \right) - x - 2 = 0\)
Điều kiện: \(x > - 1\)
Ta có:
\(\begin{array}{l}m{\ln ^2}\left( {x + 1} \right) - \left( {x + 2 - m} \right)\ln \left( {x + 1} \right) - x - 2 = 0\\ \Leftrightarrow m{\ln ^2}\left( {x + 1} \right) - \left( {x + 2} \right)\ln \left( {x + 1} \right) + m\ln \left( {x + 1} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow m\ln \left( {x + 1} \right)\left[ {\ln \left( {x + 1} \right) + 1} \right] - \left( {x + 2} \right)\left[ {\ln \left( {x + 1} \right) + 1} \right] = 0\\ \Leftrightarrow \left[ {\ln \left( {x + 1} \right) + 1} \right]\left[ {m\ln \left( {x + 1} \right) - x - 2} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}\ln \left( {x + 1} \right) + 1 = 0\\m\ln \left( {x + 1} \right) - x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 1 = {e^{ - 1}}\\m\ln \left( {x + 1} \right) - x - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {e^{ - 1}} - 1 < 0\,\,\,\left( L \right)\\m\ln \left( {x + 1} \right) - x - 2 = 0\,\,\,\left( * \right)\end{array} \right.\end{array}\)
Với \(m = 0\) thì phương trình \(\left( * \right)\) có nghiệm \(x = - 2 < - 1\left( L \right)\) nên không thỏa bài toán.
Với \(m \ne 0\) thì \(\left( * \right) \Leftrightarrow \dfrac{{\ln \left( {1 + x} \right)}}{{x + 2}} = \dfrac{1}{m}\).
Xét \(f\left( x \right) = \dfrac{{\ln \left( {1 + x} \right)}}{{x + 2}}\) có \(f'\left( x \right) = \dfrac{{\dfrac{{x + 2}}{{x + 1}} - \ln \left( {x + 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = 0 \Leftrightarrow x = {x_0} \in \left( {2;3} \right)\) và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\ln \left( {1 + x} \right)}}{{x + 2}} = 0\) nên ta có bảng biến thiên trên \(\left( { - 1; + \infty } \right)\) như sau:
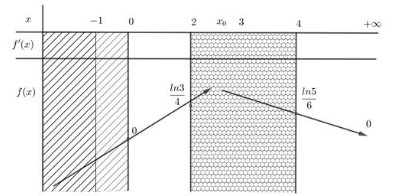
Để phương trình có nghiệm \({x_1},{x_2}\) thỏa \(0 < {x_1} < 2 < 4 < {x_2}\) thì \(0 < \dfrac{1}{m} < \dfrac{{\ln 5}}{6} \Leftrightarrow m > \dfrac{6}{{\ln 5}} \approx 3,728\)
Suy ra \(a = \dfrac{6}{{\ln 5}} \in \left( {3,7;3,8} \right)\).
Tập nghiệm của phương trình \({\log _2}\left( {{x^2} - x + 2} \right) = 1\)
Điều kiện: \({x^2} - x + 2 > 0\) (luôn đúng với \(\forall x\))
Khi đó phương trình tương đương \({x^2} - x + 2 = 2 \Leftrightarrow {x^2} - x = 0 \Leftrightarrow x\left( {x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {0;1} \right\}\).
Đề thi THPT QG 2019 – mã đề 104
Cho phương trình \(\left( {2\log _3^2x - {{\log }_3}x - 1} \right)\sqrt {{4^x} - m} = 0\) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt ?
ĐK: \(\left\{ \begin{array}{l}x > 0\\{4^x} - m \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ge {\log _4}m\,\,\left( {Do\,\,m > 0} \right)\end{array} \right.\).
\(\begin{array}{l}\left( {2\log _3^2x - {{\log }_3}x - 1} \right)\sqrt {{4^x} - m} = 0 \Leftrightarrow \left[ \begin{array}{l}2\log _3^2x - {\log _3}x - 1 = 0\\{4^x} = m\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x = - \dfrac{1}{2}\\{4^x} = m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{1}{{\sqrt 3 }}\\{4^x} = m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{1}{{\sqrt 3 }}\\x = {\log _4}m\end{array} \right.\end{array}\)
Biểu diễn các nghiệm trên trục số ta có:
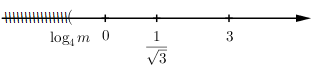
Phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}{\log _4}m = 0\\\dfrac{1}{{\sqrt 3 }} \le {\log _4}m < 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\2,26 \le m < 64\end{array} \right.\).
Lại có \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;3;4;5;...;63} \right\}\). Vậy có 62 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Đề thi THPT QG – 2021 lần 1– mã 104
Nghiệm của phương trình \({\log _2}\left( {5x} \right) = 3\) là
ĐKXĐ: \(x > 0\)
Ta có: \({\log _2}\left( {5x} \right) = 3 \Leftrightarrow 5x = {2^3} = 8 \Leftrightarrow x = \dfrac{8}{5}\,\left( {TMDK} \right)\)
Phương trình \({\log _3}\left( {3x + 6} \right) = 4\) có nghiệm là
Ta có: \({\log _3}\left( {3x + 6} \right) = 4\)
Điều kiện: \(3x + 6 > 0\) \( \Leftrightarrow x > - 2.\)
\(\begin{array}{l}\,\,\,\,\,\,{\log _3}\left( {3x + 6} \right) = 4\\ \Leftrightarrow 3x + 6 = {3^4}\\ \Leftrightarrow 3x + 6 = 81\\ \Leftrightarrow 3x = 75\\ \Leftrightarrow x = 25\,\,\left( {tm} \right)\end{array}\)
Vậy phương trình đã cho có nghiệm: \(x = 25.\)
Đề thi THPT QG - 2021 - mã 101
Nghiệm của phương trình \({\log _3}\left( {5x} \right) = 2\) là:
\({\log _3}\left( {5x} \right) = 2 \Leftrightarrow 5x = {3^2} \Leftrightarrow x = \dfrac{9}{5}\).
Tính tổng tất cả các nghiệm thực của phương trình \({\log _{\sqrt 3 }}\left( {x - 2} \right) + {\log _3}{\left( {x - 4} \right)^2} = 0.\)
ĐK : \(x > 2;x \ne 4\)
Ta có
\(\begin{array}{l}{\log _{\sqrt 3 }}\left( {x - 2} \right) + {\log _3}{\left( {x - 4} \right)^2} = 0 \Leftrightarrow {\log _3}{\left( {x - 2} \right)^2} + {\log _3}{\left( {x - 4} \right)^2} = 0\\ \Leftrightarrow {\log _3}{\left( {x - 2} \right)^2}{\left( {x - 4} \right)^2} = 0 \Leftrightarrow {\left( {x - 2} \right)^2}{\left( {x - 4} \right)^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}\left( {x - 2} \right)\left( {x - 4} \right) = 1\,\,\,\,\\\left( {x - 2} \right)\left( {x - 4} \right) = - 1\,\,\,\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} - 6x + 7 = 0\\{x^2} - 6x + 9 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3 + \sqrt 2 \,\,\,\left( {tm} \right)\\x = 3 - \sqrt 2 \,\,\,\left( {ktm} \right)\\x = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy tổng các nghiệm là \(3 + 3 + \sqrt 2 = 6 + \sqrt 2 .\)
Tập nghiệm của phương trình \({\log _2}\left( {{x^2} - 1} \right) = {\log _2}2x\) là:
Điều kiện: $\left\{ \begin{array}{l}{x^2} - 1 > 0\\2x > 0\end{array} \right. \Leftrightarrow x > 1$.
Với điều kiện này thì phương trình đã cho tương đương với
${x^2} - 1 = 2x \Leftrightarrow {x^2} - 2x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt 2 {\rm{ }}\left( {TM} \right)\\x = 1 - \sqrt 2 {\rm{ }}\left( L \right)\end{array} \right.$.
Vậy tập nghiệm của phương trình đã cho là $S = \left\{ {1 + \sqrt 2 } \right\}$
Phương trình \({\log _3}\left( {{x^2} - 9} \right) = 2\) có các nghiệm là
Ta có : \({\log _3}\left( {{x^2} - 9} \right) = 2 \Leftrightarrow {x^2} - 9 = {3^2} \Leftrightarrow {x^2} = 18 \Leftrightarrow x = \pm 3\sqrt 2 \).
Nghiệm của phương trình \({\log _3}\left( {x + 5} \right) = 2\) là:
\({\log _3}\left( {x + 5} \right) = 2 \Leftrightarrow x + 5 = 9 \Leftrightarrow x = 4\)
Cho phương trình \(2{\log _4}\left( {2{x^2} - x + 2m - 4{m^2}} \right) + {\log _{\dfrac{1}{2}}}\left( {{x^2} + mx - 2{m^2}} \right) = 0.\) Tìm tất cả các giá trị của tham số \(m\) sao cho phương trình đã cho có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn \(x_1^2 + x_2^2 > 1.\)
ĐK: \({x^2} + mx - 2{m^2} > 0 \Leftrightarrow \left( {x - m} \right)\left( {x + m} \right) + m\left( {x - m} \right) > 0 \Leftrightarrow \left( {x - m} \right)\left( {x + 2m} \right) > 0\)
Ta có \(2{\log _4}\left( {2{x^2} - x + 2m - 4{m^2}} \right) + {\log _{\dfrac{1}{2}}}\left( {{x^2} + mx - 2{m^2}} \right) = 0\)
\(\begin{array}{l} \Leftrightarrow {\log _2}\left( {2{x^2} - x + 2m - 4{m^2}} \right) = {\log _2}\left( {{x^2} + mx - 2{m^2}} \right)\\ \Rightarrow 2{x^2} - x + 2m - 4{m^2} = {x^2} + mx - 2{m^2}\\ \Leftrightarrow {x^2} - \left( {m + 1} \right)x - 2{m^2} + 2m = 0\,\,\left( * \right)\end{array}\)
Xét \(\Delta = {\left( {m + 1} \right)^2} - 4\left( { - 2{m^2} + 2m} \right) = 9{m^2} - 6m + 1 = {\left( {3m - 1} \right)^2}\)
Vì phương trình có hai nghiệm phân biệt \({x_1};{x_2}\) nên \(\Delta > 0 \Leftrightarrow {\left( {3m - 1} \right)^2} > 0 \Leftrightarrow m \ne \dfrac{1}{3}\,\,\left( 1 \right)\)
Theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 1\\{x_1}.{x_2} = - 2{m^2} + 2m\end{array} \right.\)
Ta có
\(\begin{array}{l}x_1^2 + x_2^2 > 1 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} > 1\\ \Leftrightarrow {\left( {m + 1} \right)^2} - 2\left( { - 2{m^2} + 2m} \right) > 1\\ \Leftrightarrow 5{m^2} - 2m > 0 \Leftrightarrow \left[ \begin{array}{l}m > \dfrac{2}{5}\\m < 0\end{array} \right.\,\,\,\left( 2 \right)\end{array}\)
Lại có hai nghiệm của phương trình (*) là \({x_1} = \dfrac{{ - b' + \sqrt {\Delta '} }}{a} = 2m;\,\,\,{x_2} = \dfrac{{ - b' - \sqrt {\Delta '} }}{a} = 1 - m\)
Thay vào điều kiện ban đầu \(\left( {x - m} \right)\left( {x + 2m} \right) > 0\) ta được \(\left\{ \begin{array}{l}m.4m > 0\\\left( {1 - 2m} \right)\left( {1 + m} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\ - 1 < m < \dfrac{1}{2}\end{array} \right.\left( 3 \right)\)
Kết hợp (1); (2); (3) ta được \(\left[ \begin{array}{l} - 1 < m < 0\\\dfrac{2}{5} < m < \dfrac{1}{2}\end{array} \right.\)
Tổng các nghiệm của phương trình \(\log _2^2x + {\log _2}x - 2 = 0\) bằng
ĐKXĐ: \(x > 0\).
Ta có: \(\log _2^2x + {\log _2}x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{\log _2}x = 1\\{\log _2}x = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \dfrac{1}{4}\end{array} \right.\,\,\left( {tm} \right)\)
Vậy tổng các nghiệm của phương trình là \(2 + \dfrac{1}{4} = \dfrac{9}{4}\).
Phương trình \({\log _3}\left( {5x + 2} \right) = 3\) có nghiệm là
Bước 1:
ĐK: \(x>-\dfrac{2}{5}\)
Bước 2:
Ta có:
\(\begin{array}{l}{\log _3}\left( {5x + 2} \right) = 3\\ \Leftrightarrow 5x + 2 = {3^3}\\ \Leftrightarrow 5x + 2 = 27\\ \Leftrightarrow 5x = 25\\ \Leftrightarrow x = 5\,\,\,\,\,\left( {tm} \right)\end{array}\)
Vậy nghiệm của phương trình đã cho là \(x = 5.\)

