Định lý Pytago

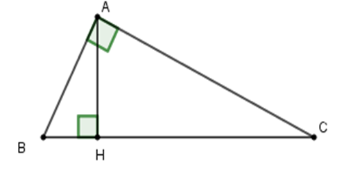
Ta có \(BC = BH + HC = 9 + 16 = 25\,cm\)

Xét tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có

\(A{B^2} + A{C^2} = B{C^2}\)\( \Rightarrow A{B^2} = B{C^2} - A{C^2}\)\( = {25^2} - {20^2} = 225\)\( \Rightarrow AB = 15\,cm.\)

Xét tam giác \(ABH\) vuông tại \(H\), theo định lý Py-ta-go ta có

\(H{B^2} + H{A^2} = A{B^2}\)\( \Rightarrow A{H^2} = A{B^2} - H{B^2} = {15^2} - {9^2} = 144\)\( \Rightarrow AH = 12\,cm.\)

Vậy \(AH = 12\,cm;\,AB = 15\,cm.\)

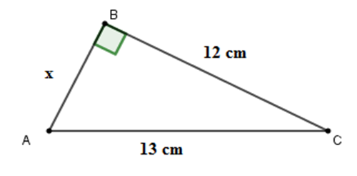
Áp dụng định lý Py-ta-go cho tam giác \(ABC\) vuông tại \(B\) ta được

\(A{C^2} = A{B^2} + A{C^2}\)\( \Rightarrow A{B^2} = A{C^2} - B{C^2}\)\( \Rightarrow {x^2} = {13^2} - {12^2} = 25 \Rightarrow x = 5\,cm.\)

Vậy \(x = 5\,cm.\)

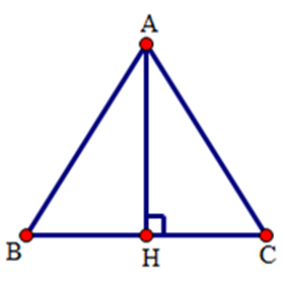
Áp dụng định lý Pitago vào tam giác $ABH$ vuông tại $H$ ta có:

\(A{B^2} = B{H^2} + A{H^2} \)\(\Leftrightarrow A{H^2} = A{B^2} - B{H^2}\)

\( \Leftrightarrow A{H^2} = {4^2} - {2^2} = 12 \)\(\Rightarrow AH = \sqrt {12} \,\,\left( {cm} \right)\)

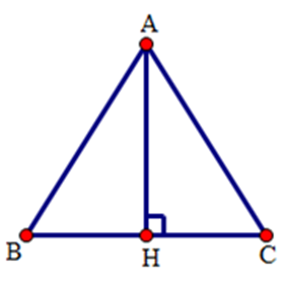
Xét tam giác $ABC$  cân tại $A$  có $AH$  là đường cao.

 Suy ra $AH$  đồng thời là đường trung tuyến.

Suy ra $BC = 2.BH = 2.2 = 4cm.$

Vậy chu vi tam giác $ABC$  là: $4 + 4 + 4 = 12\left( {cm} \right)$

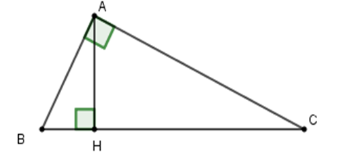
Áp dụng định lý Py-ta-go cho tam giác \(ABH\) vuông tại \(H\) ta được

\(A{H^2} + H{B^2} = A{B^2}\)\( \Rightarrow H{B^2} = A{B^2} - A{H^2} = {5^2} - {4^2} = 9\)\( \Rightarrow HB = 3\,cm\)

Suy ra \(BC = HB + HC = 3 + \sqrt {184} \,cm\)

Áp dụng định lý Pytago cho tam giác vuông \(AHC\) ta được

 \(A{C^2} = A{H^2} + H{C^2} = {4^2} + 184 = 200\)\( \Rightarrow AC = \sqrt {200} \,cm\)

Chu vi tam giác \(ABC\) là \(AB + AC + BC = 5 + \sqrt {200}  + 3 + \sqrt {184} \)\( \approx 35,7\,cm.\)

+ Với bộ số $15cm;8cm;18cm$ ta thấy \({18^2} = 324;\,{15^2} = 225;{8^2} = 64\) nên ${15^2} + {8^2} = 289 < {18^2}$ nên loại A.

+ Với bộ số $21dm;20dm;29dm$ ta thấy \({29^2} = 841;\,{21^2} = 441;\,{20^2} = 400\) nên \({21^2} + {20^2} = {29^2}\left( {441 + 400 = 881} \right)\)

Hay tam giác với ba cạnh có độ dài $21dm;20dm;29dm$ thì tam giác đó là tam giác vuông (theo định lý Pytago đảo).

+ Với bộ số $5m;6m;8m$ ta thấy \({8^2} = 64;{5^2} + {6^2} = 61 \Rightarrow {8^2} > {5^2} + {6^2}\) nên  loại C.

+ Với bộ số $2m;3m;4m$ ta thấy \({4^2} = 16;{2^2} + {3^2} = 13\) nên \({4^2} > {2^2} + {3^2}\) nên loại D.

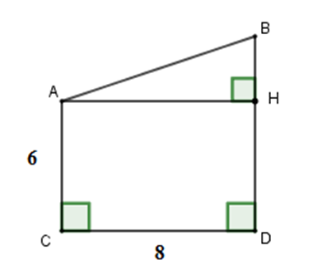
Kẻ \(AH \bot BD\) tại \(H.\)

Khi đó \(ACDB\) là hình chữ nhật suy ra \(HD = AC = 6;\,AH = CD = 8\)

Do đó \(BH = BD - DH = 10 - 6 = 4\,\)

Áp dụng định lý Py-ta-go cho tam giác vuông \(AHB\) ta được

\(A{B^2} = A{H^2} + H{B^2} = {4^2} + {8^2} = 80\)\( \Rightarrow AB = \sqrt {80} .\)

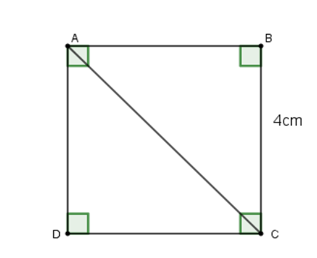
Vì \(ABCD\) là hình vuông nên \(AB = BC = 4\,cm\)

Áp dụng định lý Py-ta-go cho tam giác \(ABC\) vuông tại \(B\) ta có:

\(A{C^2} = A{B^2} + B{C^2}\) \( = {4^2} + {4^2} = 32 \Rightarrow AC = \sqrt {32} \) cm.

Gọi độ dài hai cạnh góc vuông là \(x;y\,\left( {y > x > 0} \right)\) (cm) và độ dài cạnh huyền là \(z\,\left( {z > y} \right)\,\left( {cm} \right)\)

Theo đề bài ta có \(\dfrac{x}{3} = \dfrac{y}{4}\) và \(x + y + z = 36\,cm\)

Đặt \(\dfrac{x}{3} = \dfrac{y}{4} = k\,\left( {k > 0} \right)\) suy ra \(x = 3k;\,y = 4k\)

Theo định lý Pytago ta có \({x^2} + {y^2} = {z^2}\)\( \Rightarrow {z^2} = {\left( {3k} \right)^2} + {\left( {4k} \right)^2} = 25{k^2} = {\left( {5k} \right)^2}\)\( \Rightarrow z = 5k\)

Suy ra \(x + y + z = 3k + 4k + 5k = 12k = 36\) \( \Rightarrow k = 3\) (tm )

Từ đó \(x = 9\,cm;\,y = 12\,cm;z = 15\,cm.\)

Vậy cạnh huyền dài \(15\,cm.\)

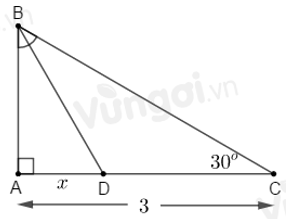
\(\Delta ABC\) vuông tại \(A\) nên \(\widehat {ABC} + \widehat {ACB} = {90^o}\) \( \Rightarrow \widehat {ABC} = {90^o} - \widehat {ACB} = {90^o} - {30^o} = {60^o}.\)

Lại có: \(BD\) là tia phân giác của \(\widehat {ABC}\) (gt) nên \(\widehat {ABD} = \widehat {DBC} = \dfrac{{\widehat {ABC}}}{2} = \dfrac{{{{60}^o}}}{2} = {30^o}.\)

\(\Delta ABC\) vuông tại \(A\) có: \(\widehat {ACB} = {30^o}\) nên \(AB = \dfrac{1}{2}BC\) hay \(BC = 2AB.\)

Áp dụng định lí Pytago vào \(\Delta ABC\) vuông tại \(A\) ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow {\left( {2AB} \right)^2} = A{B^2} + {3^2}\\ \Rightarrow 4A{B^2} = A{B^2} + 9\\ \Rightarrow 4A{B^2} - A{B^2} = 9\\ \Rightarrow 3A{B^2} = 9\\ \Rightarrow A{B^2} = 9:3 = 3\\ \Rightarrow AB = \sqrt 3 \end{array}\)

\(\Delta ABD\) vuông tại \(A\) có: \(\widehat {ABD} = {30^o}\) nên \(AD = \dfrac{1}{2}BD\) hay \(BD = 2AD.\)

Áp dụng định lí Pytago vào \(\Delta ABD\) vuông tại \(A\) ta có:

\(\begin{array}{l}B{D^2} = A{B^2} + A{D^2}\\ \Rightarrow {\left( {2AD} \right)^2} = A{B^2} + A{D^2}\\ \Rightarrow {\left( {2x} \right)^2} = {\left( {\sqrt 3 } \right)^2} + {x^2}\\ \Rightarrow 4{x^2} = 3 + {x^2}\\ \Rightarrow 4{x^2} - {x^2} = 3\\ \Rightarrow 3{x^2} = 3\\ \Rightarrow {x^2} = 3:3 = 1\\ \Rightarrow x = \sqrt 1  = 1\end{array}\).

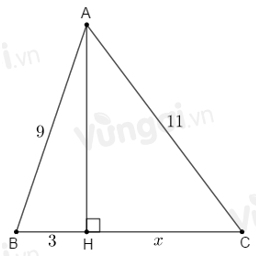
Áp dụng định lí Pytago vào \(\Delta {\rm{A}}BH\) vuông tại \(H\) ta có:

\(A{B^2} = A{H^2} + B{H^2}\)

\( \Rightarrow A{H^2} = A{B^2} - B{H^2} = {9^2} - {3^2} = 72\).

Áp dụng định lí Pytago vào \(\Delta {\rm{AC}}H\) vuông tại \(H\) ta có:

\(A{C^2} = A{H^2} + H{C^2}\)

\( \Rightarrow H{C^2} = A{C^2} - A{H^2} = {11^2} - 72 = 49\)

\( \Rightarrow x = HC = \sqrt {49}  = 7.\)

Áp dụng định lí Pytago vào tam giác vuông \(AHB\) vuông tại \(H\) ta có:

\(A{H^2} + B{H^2} = A{B^2} \Rightarrow A{H^2} = A{B^2} - B{H^2}\)     (1)

Áp dụng định lí Pytago vào tam giác vuông \(AHC\) vuông tại \(H\) ta có:

\(A{H^2} + C{H^2} = A{C^2} \Rightarrow A{H^2} = A{C^2} - C{H^2}\)     (2)

Từ (1) và (2) ta có: \(A{B^2} - B{H^2} = A{C^2} - C{H^2}\)

\( \Rightarrow A{B^2} - {18^2} = {x^2} - {32^2}\)

\( \Rightarrow A{B^2} = {x^2} - {32^2} + {18^2}\)

\( \Rightarrow A{B^2} = {x^2} - 1024 + 324\)

\( \Rightarrow A{B^2} = {x^2} - 700\)

Ta có: \(BC = BH + CH = 18 + 32 = 50.\)

Áp dụng định lí Pytago vào tam giác vuông \(ABC\) vuông tại \(A\) ta có:

\(A{B^2} + A{C^2} = B{C^2}\)

\( \Rightarrow A{B^2} + {x^2} = {50^2}\)       (3)

Thay \(A{B^2} = {x^2} - 700\) vào (3) ta được:

\(\begin{array}{l}{x^2} - 700 + {x^2} = {50^2}\\ \Rightarrow 2{x^2} = 2500 + 700\\ \Rightarrow 2{x^2} = 3200\\ \Rightarrow {x^2} = 3200:2 = 1600\\ \Rightarrow x = \sqrt {1600}  = 40.\end{array}\).

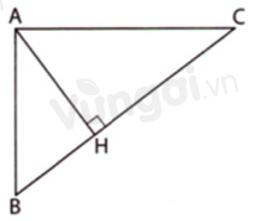
Áp dụng định lí Pytago vào tam giác vuông \(AHB\) vuông tại \(H\) ta có:

\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2}\\ \Rightarrow A{B^2} = {6^2} + 4,{5^2} = 36 + \dfrac{{81}}{4} = \dfrac{{225}}{4}\end{array}\)

Áp dụng định lí Pytago vào tam giác vuông \(AHC\) vuông tại \(H\) ta có:

\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\ \Rightarrow A{C^2} = {6^2} + {8^2} = 36 + 64 = 100\end{array}\)

Ta có: \(BC = BH + HC = 4,5 + 8 = \dfrac{{25}}{2}\)

\( \Rightarrow B{C^2} = {\left( {\dfrac{{25}}{2}} \right)^2} = \dfrac{{625}}{4}\)                             (1)

Ta có: \(A{B^2} + A{C^2} = \dfrac{{225}}{4} + 100 = \dfrac{{625}}{4}\)       (2)

Từ (1) và (2) suy ra: \(B{C^2} = A{B^2} + A{C^2}\)

Vậy tam giác \(ABC\) vuông tại \(A.\)

Gọi \({\rm{a}},b,c\) lần lượt là độ dài ba cạnh của tam giác ứng với các đường cao theo thứ tự đã cho, \(S\) là diện tích của \(\Delta ABC\)  \(\left( {a,b,c,\,S > 0} \right).\)

Ta có: \(S = \dfrac{1}{2}.4,8.a = \dfrac{1}{2}.6.b = \dfrac{1}{2}.8.c\) hay \(4,8a = 6b = 8c = 2S\)

Do đó \(a = \dfrac{{2S}}{{4,8}} = \dfrac{{5S}}{{12}}\), \(b = \dfrac{{2S}}{6} = \dfrac{S}{3}\), \(c = \dfrac{{2S}}{8} = \dfrac{S}{4}\).

Ta có: \({b^2} + {c^2} = {\left( {\dfrac{S}{3}} \right)^2} + {\left( {\dfrac{S}{4}} \right)^2} = \dfrac{{{S^2}}}{9} + \dfrac{{{S^2}}}{{16}} = \dfrac{{25{S^2}}}{{144}}\), \({a^2} = {\left( {\dfrac{{5S}}{{12}}} \right)^2} = \dfrac{{25{S^2}}}{{144}}\).

Suy ra \({a^2} = {b^2} + {c^2}\) nên tam giác đã cho là tam giác vuông, đỉnh góc vuông ứng với đường cao có độ dài là \(4,8\,cm.\)