Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(\widehat B;\widehat C\) là các góc nhọn. Gọi \(H\) là chân đường vuông góc hạ từ \(A\) xuống \(BC\). Biết \(AH = 6cm;BH = 4,5cm\) và \(HC = 8cm.\) Khi đó \(\Delta ABC\) là tam giác gì?
Trả lời bởi giáo viên
Đáp án đúng: b
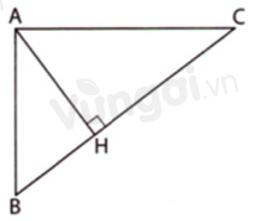
Áp dụng định lí Pytago vào tam giác vuông \(AHB\) vuông tại \(H\) ta có:
\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2}\\ \Rightarrow A{B^2} = {6^2} + 4,{5^2} = 36 + \dfrac{{81}}{4} = \dfrac{{225}}{4}\end{array}\)
Áp dụng định lí Pytago vào tam giác vuông \(AHC\) vuông tại \(H\) ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\ \Rightarrow A{C^2} = {6^2} + {8^2} = 36 + 64 = 100\end{array}\)
Ta có: \(BC = BH + HC = 4,5 + 8 = \dfrac{{25}}{2}\)
\( \Rightarrow B{C^2} = {\left( {\dfrac{{25}}{2}} \right)^2} = \dfrac{{625}}{4}\) (1)
Ta có: \(A{B^2} + A{C^2} = \dfrac{{225}}{4} + 100 = \dfrac{{625}}{4}\) (2)
Từ (1) và (2) suy ra: \(B{C^2} = A{B^2} + A{C^2}\)
Vậy tam giác \(ABC\) vuông tại \(A.\)
Hướng dẫn giải:
- Áp dụng
+ Định lý Py-ta-go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
+ Định lý Pytago đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phường của hai cạnh kia thì tam giác đó là tam giác vuông.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
