Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông ở \(A\) có: \(AC = 8cm.\) Kẻ \(AH\) vuông góc với \(BC.\) Biết \(BH = 3,6cm, HC = 6,4cm.\) Tính \(AB,AH.\)
Trả lời bởi giáo viên
Đáp án đúng: a
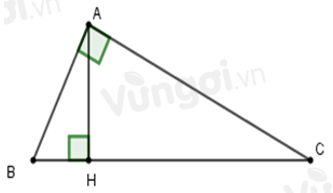
Ta có: \(BC = BH + HC = 3,6 + 6,4 = 10\,cm\).
Xét tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Rightarrow A{B^2} = B{C^2} - A{C^2}\)\( = {10^2} - {8^2} = 100 - 64 = 36\)
\( \Rightarrow AB = \sqrt {36} = 6\,cm.\)
Xét tam giác \(ABH\) vuông tại \(H\), theo định lý Py-ta-go ta có:
\(H{B^2} + H{A^2} = A{B^2}\)
\( \Rightarrow A{H^2} = A{B^2} - H{B^2} = {6^2} - 3,{6^2} = 23,04\)
\( \Rightarrow AH = \sqrt {23,04} = 4,8\,cm.\)
Vậy \(AH = 4,8\,cm;\,AB = 6\,cm.\)
Hướng dẫn giải:
Áp dụng định lý Pytago: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
