Câu hỏi:
2 năm trước
Cho tam giác $ABC,$ kẻ $AH$ vuông góc với $BC.$ Tính chu vi \(\Delta ABC\) biết $AB = 5cm,$ $AH = 4cm,HC = \sqrt {184} cm$ (làm tròn đến chữ số thập phân thứ nhất).
Trả lời bởi giáo viên
Đáp án đúng: b
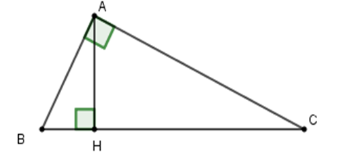
Áp dụng định lý Py-ta-go cho tam giác \(ABH\) vuông tại \(H\) ta được
\(A{H^2} + H{B^2} = A{B^2}\)\( \Rightarrow H{B^2} = A{B^2} - A{H^2} = {5^2} - {4^2} = 9\)\( \Rightarrow HB = 3\,cm\)
Suy ra \(BC = HB + HC = 3 + \sqrt {184} \,cm\)
Áp dụng định lý Pytago cho tam giác vuông \(AHC\) ta được
\(A{C^2} = A{H^2} + H{C^2} = {4^2} + 184 = 200\)\( \Rightarrow AC = \sqrt {200} \,cm\)
Chu vi tam giác \(ABC\) là \(AB + AC + BC = 5 + \sqrt {200} + 3 + \sqrt {184} \)\( \approx 35,7\,cm.\)
Hướng dẫn giải:
Áp dụng định lý Py-ta-go tính các cạnh của tam giác \(ABC\)
Từ đó tính chu vi tam giác \(ABC.\)
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
