Tính $x$ trong hình vẽ sau:

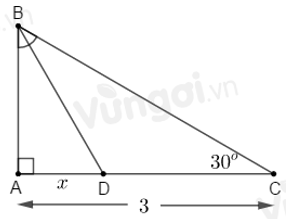
$\Delta ABC$ vuông tại $A$ nên $\widehat {ABC} + \widehat {ACB} = {90^o}$ $\Rightarrow \widehat {ABC} = {90^o} - \widehat {ACB} = {90^o} - {30^o} = {60^o}.$

Lại có: $BD$ là tia phân giác của $\widehat {ABC}$ (gt) nên $\widehat {ABD} = \widehat {DBC} = \dfrac{{\widehat {ABC}}}{2} = \dfrac{{{{60}^o}}}{2} = {30^o}.$

$\Delta ABC$ vuông tại $A$ có: $\widehat {ACB} = {30^o}$ nên $AB = \dfrac{1}{2}BC$ hay $BC = 2AB.$

Áp dụng định lí Pytago vào $\Delta ABC$ vuông tại $A$ ta có:

$\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow {\left( {2AB} \right)^2} = A{B^2} + {3^2}\\ \Rightarrow 4A{B^2} = A{B^2} + 9\\ \Rightarrow 4A{B^2} - A{B^2} = 9\\ \Rightarrow 3A{B^2} = 9\\ \Rightarrow A{B^2} = 9:3 = 3\\ \Rightarrow AB = \sqrt 3 \end{array}$

$\Delta ABD$ vuông tại $A$ có: $\widehat {ABD} = {30^o}$ nên $AD = \dfrac{1}{2}BD$ hay $BD = 2AD.$

Áp dụng định lí Pytago vào $\Delta ABD$ vuông tại $A$ ta có:

$\begin{array}{l}B{D^2} = A{B^2} + A{D^2}\\ \Rightarrow {\left( {2AD} \right)^2} = A{B^2} + A{D^2}\\ \Rightarrow {\left( {2x} \right)^2} = {\left( {\sqrt 3 } \right)^2} + {x^2}\\ \Rightarrow 4{x^2} = 3 + {x^2}\\ \Rightarrow 4{x^2} - {x^2} = 3\\ \Rightarrow 3{x^2} = 3\\ \Rightarrow {x^2} = 3:3 = 1\\ \Rightarrow x = \sqrt 1  = 1\end{array}$.