Một chuyển động thẳng có đồ thị v - t như hình vẽ:
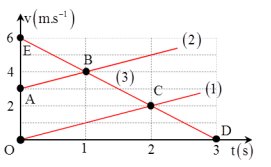
Sau bao nhiêu giây thì vật thứ 3 có vận tốc bằng vận tốc của vật thứ 2?
Ta có vật dừng lại khi v = 0
Từ đồ thị, ta có: vật thứ 3 có vận tốc bằng vận tốc của vật thứ 2 khi t = 1s
=> Sau 1s thì vật thứ 3 sẽ có vận tốc bằng vận tốc của vật thứ 2
Một xe máy đang đi với \({v_0} = 50,4km/h\) bỗng người lái xe thấy có ổ gà trước mắt cách xe \(24,5m\). Người ấy phanh gấp và xe đến ổ gà thì dừng lại. Tính gia tốc của xe và thời gian từ lúc xe hãm phanh đến khi dừng lại.
Ta có: \(\left\{ \begin{array}{l}{v_0} = 50,4km/h = 14m/s\\s = 24,5m\end{array} \right.\)
Xe dừng lại có \(v = 0\)
Áp dụng công thức liên hệ giữa s, v và a ta có:
\({v^2} - v_0^2 = 2as \Rightarrow a = \dfrac{{{v^2} - v_0^2}}{{2s}} = \dfrac{{0 - {{14}^2}}}{{2.24,5}} = - 4m/{s^2}\)
Lại có: \(v = {v_0} + at \Rightarrow t = \dfrac{{v - {v_0}}}{a} = \dfrac{{0 - 14}}{{ - 4}} = 3,5s\)
Một ô tô đang chạy với vận tốc \(54km/h\) thì hãm phanh và chuyển động chậm dần đều, sau 12 giây thì dừng lại. Quãng đường ô tô đi được trong thời gian này:
Ta có: \(\left\{ \begin{array}{l}{v_0} = 54km/h = 15m/s\\t = 12s\\v = 0\end{array} \right.\)
Gia tốc của ô tô:
\(a = \dfrac{{v - {v_0}}}{t} = \dfrac{{0 - 15}}{{12}} = - 1,25m/{s^2}\)
Áp dụng công thức liên hệ giữa s, v và a ta có:
\(s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{{0^2} - {{15}^2}}}{{2.\left( { - 1,25} \right)}} = 90m\)
Từ hai điểm A và B cách nhau \(200cm,\) hai vật chuyển động ngược chiều nhau. Vật thứ nhất từ A bắt đầu chuyển động nhanh dần đều với gia tốc \(3{\mkern 1mu} {\mkern 1mu} cm/{s^2}\), cùng lúc vật thứ hai đi ngang qua B với vận tốc \(5cm/s\) và chuyển động nhanh dần đều với gia tốc \(2{\mkern 1mu} {\mkern 1mu} cm/{s^2}\). Hãy xác định thời gian và vị trí hai vật gặp nhau.
Chọn gốc tọa độ O tại điểm A, chiều dương từ A đến B.
Chọn gốc thời gian \(t = 0\) là lúc vật thứ nhất bắt đầu chuyển động.
Phương trình chuyển động của hai vật:
\(\begin{array}{l}{x_1} = {x_{01}} + {v_{01}}t + \dfrac{{{a_1}{t^2}}}{2} = \dfrac{{3{t^2}}}{2} = 1,5{t^2}\\{x_2} = {x_{02}} + {v_{02}}t + \dfrac{{{a_2}{t^2}}}{2}\\\,\,\,\,\,\, = 200 - 5t + \dfrac{{\left( { - 2} \right){t^2}}}{2} = 200 - 5t - {t^2}\end{array}\)
Hai vật gặp nhau khi:
\({x_1} = {x_2} \Rightarrow 1,5{t^2} = 200 - 5t - {t^2} \Rightarrow \left[ {\begin{array}{*{20}{l}}{t = - 10{\mkern 1mu} {\mkern 1mu} \left( s \right)}\\{t = 8{\mkern 1mu} {\mkern 1mu} \left( s \right)}\end{array}} \right.\)
Do \(t > 0 \Rightarrow t = 8\left( s \right)\)
Vị trí hai xe gặp nhau: \({x_1} = {x_2} = 1,{5.8^2} = 96{\mkern 1mu} {\mkern 1mu} \left( m \right)\)
Từ hai điểm A và B cách nhau \(200cm\) hai vật chuyển động ngược chiều nhau. Vật thứ nhất từ A bắt đầu chuyển động nhanh dần đều với gia tốc \(3cm/s^2,\) cùng lúc vật thứ hai đi ngang qua B với vận tốc \(5cm/s\) và chuyển động nhanh dần đều với gia tốc \(2cm/s^2.\) Hãy xác định thời gian và vị trí hai vật gặp nhau?
Chọn trục Ox trùng AB, chiều dương từ A đến B, gốc tọa độ tại A, gốc thời gian là lúc hai xe bắt đầu chuyển động.
Phương trình chuyển động của hai xe là:
\(\left\{ \begin{array}{l}{x_1} = 0 + 0.t + \dfrac{1}{2}.3.{t^2} = 1,5{t^2}\,\left( {cm} \right)\\{x_2} = 200 - 5t + \dfrac{1}{2}.\left( { - 2} \right){t^2} = 200 - 5t - {t^2}\,\,\left( {cm} \right)\end{array} \right.\)
Hai vật gặp nhau khi:
\(\begin{array}{l}{x_1} = {x_2} \Leftrightarrow 1,5{t^2} = 200 - 5t - {t^2}\\ \Leftrightarrow 2,5{t^2} + 5t - 200 = 0 \Rightarrow t = 8s\end{array}\)
Vị trí gặp nhau cách A: \({x_1} = 1,5{t^2} = 1,{5.8^2} = 96\,\left( {cm} \right)\)
Một vật đang chuyển động với vận tốc \(36km/h,\) tài xế tắt máy và hãm phanh xe chuyển động chậm dần đều sau \(50m\) nữa thì dừng lại. Quãng đường xe đi được trong \(4s\) kể từ lúc bắt đầu hãm phanh là:
Gia tốc của chuyển động: \(a = \dfrac{{{v^2} - v_0^2}}{{2s}} = \dfrac{{{0^2} - {{10}^2}}}{{2.50}} = - 1m/{s^2}\)
Quãng đường mà xe đi được trong \(4s\) kể từ lúc hãm phanh là:
\(s = {v_0}t + \dfrac{1}{2}a{t^2} = 10.4 + \dfrac{1}{2}( - 1){.4^2} = 32m\)
Một vật chuyển động nhanh dần đều với vận tốc ban đầu bằng \(0.\) Trong giây thứ nhất, vật đi được quãng đường \(s = 3m.\) Trong giây thứ hai, vật đi được quãng đường bao nhiêu?
Quãng đường vật đi được trong giây thứ nhất là \(3m,\) ta có:
\({s_1} = {v_0}{t_1} + \dfrac{1}{2}at_1^2 \Leftrightarrow 0.1 + \dfrac{1}{2}a{.1^2} = 3 \Rightarrow a = 6m/{s^2}\)
Quãng đường vật đi được trong \(2s\) đầu là:
\({s_2} = 0.2 + \dfrac{1}{2}\left( 6 \right){.2^2} = 12m\)
Quãng đường vật đi được trong giây thứ hai:
\(s = {s_2} - {s_1} = 12 - 3 = 9m\)
Một ô tô đang chuyển động với vận tốc là \(10 m/s\) trên đoạn đường thẳng, thì người lái xe hãm phanh, xe chuyển động chậm dần đều với gia tốc có độ lớn \(2m/s^2.\) Quãng đường mà ô tô đi được sau thời gian \(3\) giây là:
Công thức tính quãng đường: \(s = {v_0}t + \dfrac{{a{t^2}}}{2}\)
Vật chuyển động chậm dần: \({v_0}\; = 10m/s;a = - 2m/{s^2}\)
Quãng đường ô tô đi được sau thời gian \(3s\) là:
\(s = {v_0}.t + \dfrac{1}{2}.a.{t^2} = 10.3 - \dfrac{1}{2}{.2.3^2} = 21m\)
Khi ô tô đang chạy với vận tốc 10m/s trên đoạn đường thẳng thì người lái xe hãm phanh và ô tô chuyển động chậm dần đều. Cho tới khi dừng hẳn lại thì ô tô đã chạy thêm được 100m. Gia tốc của ô tô là :
Ta có : \(\left\{ \begin{array}{l}v = 10m/s\\v = 0\\s = 100m\end{array} \right.\)
Áp dụng công thức liên hệ giữa s, v và a ta có :
\({v^2} - v_0^2 = 2as \Rightarrow a = \dfrac{{{v^2} - v_0^2}}{{2s}} = \dfrac{{0 - {{10}^2}}}{{2.100}} = - 0,5m/{s^2}\)
Một tàu dời ga chuyển động nhanh dần đều, sau 1 phút tàu đạt 54 km/h. Quãng đường tàu đi được trong giây thứ 60 là: (làm tròn đến chữ số thập phân thứ nhất)
Gia tốc của vật là \(a = \frac{{v - {v_0}}}{t} = \frac{{15 - 0}}{{60}} = 0,25m/{s^2}\)
Quãng đường vật đi được trong 60s đầu là \({s_{60}} = 0.60 + \frac{1}{2}0,{25.60^2} = 450m\)
Quãng đường vật đi được trong 59s đầu là \({s_{59}} = 0.59 + \frac{1}{2}0,{25.59^2} = 435,1m\)
Quãng đường vật đi được trong giây thứ 60 là \(s = {s_{60}} - {s_{59}} = 450 - 435,1 = 14,9m\)
Một chất điểm chuyển động theo phương trình \(S = {t^3} + 5{t^2} - 5\), trong đó \(t > 0\), t được tính bằng giây (s) và S được tính bằng mét (m). Tính vận tốc của chất điểm tại thời điểm \(t = 2\) (giây).
Ta có:
\(\begin{array}{l}v = s'\left( t \right) = 3{t^2} + 10t\\ \Rightarrow v\left( 2 \right) = {3.2^2} + 10.2 = 32\,\,\left( {m/s} \right)\end{array}\)
Một đoàn tàu bắt đầu rời ga. Chuyển động nhanh dần đều, sau $20s$ đạt đến vận tốc $36km/h$ . Hỏi sau bao lâu nữa tàu đạt được vận tốc $54km/h$?
Ta có: \(36km/h = 10m/s\)
+ Gia tốc của chuyển động: \(a = \frac{{10 - 0}}{{20}} = 0,5m/{s^2}\)
+ Phương trình vận tốc của vật: \(v = at = 0,5t\)
Thời gian để tàu đạt vận tốc \(54{\rm{ }}km/h = 15m/s\) tính từ lúc tàu đạt tốc độ 36km/h là: \(\Delta t = \frac{{15}}{{0,5}} - 20 = 30 - 20 = 10{\rm{s}}\)
Một vật chuyển động thẳng có phương trình \(x = 30 + 4t - {t^2}(m;s)\) . Tính quãng đường vật đi từ thời điểm $t_1 = 1s$ đến thời điểm $t_2 = 3s$?
Từ phương trình tọa độ - thời gian ta thu được phương trình vận tốc \(v = 4 - 2t \to v = 0 \leftrightarrow t = 2{\rm{s}}\) , vật sẽ đổi chiều chuyển động sau $2s$.
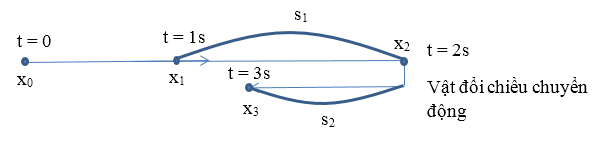
Do vậy quãng đường đi được của vật được tính:
\(s = {s_1} + {s_2} = \left| {{x_2} - {x_1}} \right| + \left| {{x_3} - {x_2}} \right| = \left| {4 - 3} \right| + \left| {3 - 4} \right| = 2m\)
Một vật đang chuyển động với vận tốc $36km/h$ , tài xế tắt máy và hãm phanh xe chuyển động chậm dần đều sau $50m$ nữa thì dừng lại. Quãng đường xe đi được trong $4s$ kể từ lúc bắt đầu hãm phanh là:
Gia tốc của chuyển động: \(a = \frac{{{0^2} - {{10}^2}}}{{2.50}} = - 1m/{s^2}\)
Quãng đường mà xe đi được trong 4 s kể từ lúc hãm phanh là: \(s = {v_0}t + \frac{1}{2}a{t^2} = 10.4 + \frac{1}{2}( - 1){.4^2} = 32m\)
Một vật chuyển động thẳng có phương trình vận tốc \(v = 2 - 2t\).Tốc độ trung bình của vật sau $4s$ kể từ lúc bắt đầu chuyển động là:
Ta để ý rằng sau $1s$ vật đã đổi chiều chuyển động
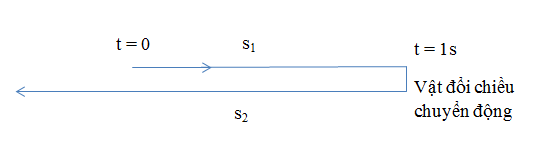
Chọn gốc thời gian là vị trí vật bắt đầu chuyển động, ta có:
Phương trình li độ của vật: \(x = {v_0}t + \dfrac{1}{2}a{t^2} = 2t - {t^2}\)
+ Tại \(t = 0\): \({x_0} = 0\)
+ Tại \(t = 1s\): \({x_1} = 1m\)
+ Tại \(t = 4s\): \({x_4} = - 8m\)
=> Ta suy ra:
+ Quãng đường vật đi được trong giây thứ nhất là: \({s_1} = {x_1} - {x_0} = 1m\)
+ Quãng đường vật đi được từ giây thứ 1 đến giây thứ 4 là: \({s_2} = \left| {{x_4} - {x_1}} \right| = \left| { - 8 - 1} \right| = 9m\)
=> Quãng đường vật đi được sau 4 s: \(s = {s_1} + {s_2} = 1 + 9 = 10m\)
Tốc độ trung bình \({v_{tb}} = \dfrac{s}{t} = \dfrac{{10}}{{1 + 3}} = 2,5m/s\)
Một vật chuyển động thẳng nhanh dần đều, trong giây thứ hai vật đi được quãng đường dài $1,5m$. Tính quãng đường vật đi được trong giây thứ $100$?
Gọi a là gia tốc của chuyển động
+ Vận tốc của vật sau giây thứ nhất là \({v_{01}} = a.1 = a\)
Quãng đường mà vật đi được trong giây thứ hai: \({s_2} = {v_{01}}t + \dfrac{1}{2}a{t^2} = a + \dfrac{a}{2} = 1,5{\rm{a = 1,5}} \to {\rm{a = 1m/}}{{\rm{s}}^2}\)
+ Vận tốc của vật sau giây thứ 99: \({v_{099}} = a.99 = 99m/s\)
Quãng đường vật đi được trong giây thứ 100: \({s_{100}} = {v_{099}}t + \dfrac{1}{2}a{t^2} = 99.1 + \dfrac{1}{2}1.1 = 99,5m\)
Phương trình nào sau đây cho biết vật chuyển động nhanh dần đều dọc theo chiều dương của trục x?
Chuyển động nhanh dần đều thì a và v cùng dấu, theo chiều dương của Ox nên a và v phải dương => Phương án C phù hợp với yêu cầu của đề bài
Vật chuyển động thẳng có phương trình \(x = 2{t^2} - 4t + 10(m;s)\) . Vật sẽ dừng lại tại vị trí :
Phương trình vận tốc của vật:
\(\begin{array}{l}v = - 4 + 4t\\v = 0 \leftrightarrow - 4 + 4t = 0 \to t = 1{\rm{s}}\end{array}\)
Vật sẽ dừng lại tại vị trí \(x = {2.1^2} - 4.1 + 10 = 8m\)
Phương trình chuyển động của một vật có dạng \(x = 3 - 4t + 2{t^2}(m;s)\). Biểu thức vận tốc tức thời của vật theo thời gian là:
Từ phương trình chuyển động ta có:
\(\left\{ \begin{array}{l}{v_0} = - 4\\a = 2.2 = 4m/{s^2}\end{array} \right.\)
=> Phương trình vận tốc: \(v = - 4 + 4t\)
Một vật chuyển động nhanh dần đều với vận tốc ban đầu $v_0 = 0$. Trong giây thứ nhất vật đi được quãng đường $s_1 = 3m$. Trong giây thứ hai vật đi được quãng đường $s_2$ bằng:
Chọn gốc tọa độ tại vị trí vật bắt đầu chuyển động
Gốc thời gian là lúc vật bắt đầu chuyển động
Ta có:
+ Phương trình chuyển động của vật là: $s = \dfrac{1}{2}a{t^2}$
+ Quãng đường vật đi được trong giây thứ nhất: \({s_1} = \dfrac{1}{2}a{.1^2} = 3 \to a = 6m/{s^2}\)
+ Quãng đường vật đi được trong hai giây đầu là \({s_2} = \dfrac{1}{2}{6.2^2} = 12m\)
=> Quãng đường vật đi được trong giây thứ 2 là: \(s = {s_2} - {s_1} = 12 - 3 = 9m\).

