Một ôtô đang chuyển động với vận tốc $54km/h$ thì hãm phanh, chuyển động chậm dần đều và dừng lại sau $10s$. Chọn chiều dương là chiều chuyển động của ôtô .Vận tốc của ôtô sau khi hãm phanh được $6s$ là:
Đổi \(54km/h = 15m/s\)
Gia tốc của xe:
\(a = \frac{{0 - 15}}{{10}} = - 1,5m/{s^2}\)
Phương trình vận tốc của vật: \(v = 15 - 1,5t\)
Vận tốc của xe sau khi hãm phanh 6 s là: \(v = 15 - 1,5.6 = 6m/s\)
Một chiếc xe hơi giảm tốc chậm dần đều từ $54km/h$ còn $36km/h$ trên quãng đường thẳng dài $125m$. Vậy gia tốc của xe trên đoạn đường này là:
Đổi \(54km/h = 15m/s,\,36km/h = 10m/s\)
Ta có: \({v^2} - v_0^2 = 2{\rm{as}} \to {\rm{a = }}\frac{{{v^2} - v_0^2}}{{2{\rm{s}}}} = \frac{{{{10}^2} - {{15}^2}}}{{2.125}} = - 0,5m/{s^2}\)
Một xe ôtô chuyển động chậm dần đều với vận tốc ban đầu \(v_0= 20m/s\) và gia tốc \(3m/s^2\). Vận tốc của xe khi đi thêm \(50m\) và quãng đường đi được cho đến khi dừng lại hẳn lần lượt có giá trị là:
Ta có: \({v^2} - v_0^2 = 2{\rm{as}}\)
Vận tốc của xe khi đi được quãng đường \(50 m\): \({v_1}^2 - v_0^2 = 2{\rm{a}}{{\rm{s}}_1} \to v = \sqrt {2{\rm{a}}{{\rm{s}}_1} + v_0^2} = \sqrt {2.( - 3).50 + {{20}^2}} = 10m/s\)
Quãng đường vật đi được cho đến khi dừng hẳn: \({v^2} - v_0^2 = 2{\rm{as}} \to s = \dfrac{{{v^2} - v_0^2}}{{2{\rm{a}}}} = \dfrac{{{0^2} - {{20}^2}}}{{2.( - 3)}} = 66,67m\)
Một đoàn tàu đang chạy với vận tốc 72km/h thì hãm phanh, chạy chậm dần đều sau 10s vận tốc giảm xuống còn 54km/h . Hỏi sau bao lâu thì tàu dừng lại hẳn
Gia tốc của xe : \(a = \frac{{15 - 20}}{{10}} = - 0,5m/{s^2}\)
Phương trình vận tốc của vật: \(v = 20 - 0,5t\)
Xe dừng lại hẳn khi: \(v = 0 \leftrightarrow 20 - 0,5t = 0 \to t = 40{\rm{s}}\)
Lúc 7 h, hai ôtô bắt đầu khởi hành từ hai điểm A, B cách nhau 2400 m, chuyển động nhanh dần đều và ngược chiều nhau. ôtô đi từ A có gia tốc 1 m/s2, còn ôtô từ B có gia tốc 2 m/s2. Chọn chiều dương hướng từ A đến B, gốc thời gian lúc 7 h. Xác định vị trí hai xe gặp nhau:
Ta có:
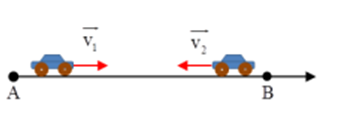
+ Phương trình chuyển động của hai ô tô lúc này là: \(\left\{ \begin{array}{l}A:{x_1} = \dfrac{1}{2}{t^2}\\B:{x_2} = 2400 - {t^2}\end{array} \right.\)
+ Khi hai xe gặp nhau: \({x_1} = {x_2} \leftrightarrow \dfrac{1}{2}{t^2} = 2400 - {t^2} \to t = 40{\rm{s}}\)
Vậy vị trí hai xe gặp cách A một khoảng: \(x = {x_1}(t = 40{\rm{s}}) = \dfrac{1}{2}{.40^2} = 800m\)
Cùng một lúc tại hai điểm $A, B$ cách nhau $125 m$ có hai vật chuyển động ngược chiều nhau. Vật đi từ $A$ có vận tốc đầu $4 m/s$ và gia tốc là $2 m/{s^2}$, vật đi từ B có vận tốc đầu $6 m/s$ và gia tốc $4 m/{s^2}$. Biết các vật chuyển động nhanh dần đều. Chọn $A$ làm gốc tọa độ, chiều dương hướng từ $A$ đến $B$, gốc thời gian lúc hai vật cùng xuất phát. Xác định thời điểm hai vật gặp nhau?
Ta có:
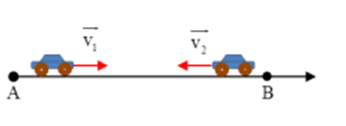
+ Phương trình chuyển động của hai ô tô lúc này là: \(\left\{ \begin{array}{l}A:{x_1} = 4t + {t^2}\\B:{x_2} = 125 - 6t - 2{t^2}\end{array} \right.\)
+ Khi hai xe gặp nhau:
\(\begin{array}{l}{x_1} = {x_2} \leftrightarrow 4t + {t^2} = 125 - 6t - 2{t^2}\\ \leftrightarrow 3{t^2} + 10t - 125 = 0\\ \to \left[ \begin{array}{l}t = 5{\rm{s}}\\t = - \frac{{25}}{3}(L)\end{array} \right.\end{array}\)
Vậy thời điểm $2$ xe gặp nhau là $5s$
Một xe ôtô đi từ Ba La vào trung tâm Hà Nội có đồ thị v-t như hình vẽ:
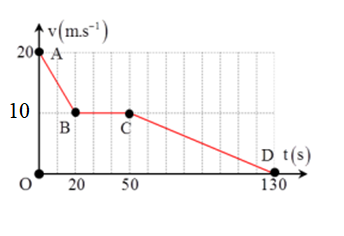
Quãng đường mà ôtô đi được là:
Ta có:
+ Trên đoạn \(A \to B\) xe chuyển động chậm dần đều với gia tốc: \({a_1} = \frac{{{v_B} - {v_A}}}{{\Delta t}} = \frac{{10 - 20}}{{20}} = - 0,5m/{s^2}\)
Quãng đường vật đi được: \({s_1} = 20t - 0,25{t^2} = 20.20 - 0,{25.20^2} = 300m\)
+ Trên đoạn \(B \to C\) xe chuyển động thẳng đều với vận tốc \(v = 10m/s\)
Quãng đường vật đi được: \({s_2} = vt = 10.30 = 300m\)
+ Trên đoạn \(C \to D\) xe chuyển động chậm dần đều với gia tốc:
\({a_3} = \frac{{0 - 10}}{{130 - 50}} = - 0,125m/s{}^2\)
Quãng đường vật đi được: \({s_3} = 10t - 0,0625{t^2} = 10.80 - 0,{0625.80^2} = 400m\)
Vậy quãng đường mà ôtô đi được là: \(s = {s_1} + {s_2} + {s_3} = 300 + 300 + 400 = 1000m\)
Cho đồ thị v - t của hai ôtô như hình vẽ:
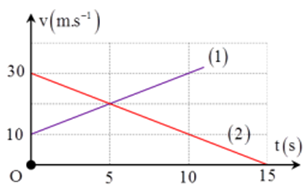
Giao điểm của đồ thị cho biết:
Giao điểm của đồ thị cho biết thời điểm 2 xe có cùng tốc độ
Cho đồ thị v - t của hai ôtô như hình vẽ:
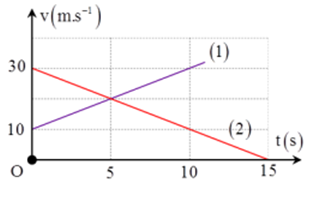
Chọn phương án đúng?
Từ đồ thị ta suy ra,
+ Phương trình vận tốc của oto 1 là: \({v_1} = 10 + 2t\)
+ phương trình vận tốc của oto 2 là: \({v_2} = 30 - 2t\)
Một chất điểm chuyển động thẳng có đồ thị vận tốc - thời gian như hình vẽ. Trong suốt quá trình chuyển động, tốc độ trung bình là 9 m/s. Phương trình chuyển động của chất điểm khi đi từ B đến C là?
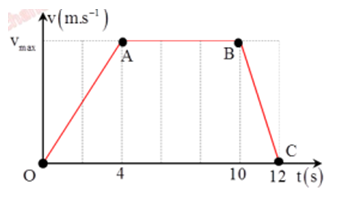
Ta có :
+ Tốc độ trung bình của vật : \({v_{tb}} = \dfrac{s}{t} = \dfrac{{\dfrac{1}{2}{v_{{\rm{max}}}}.4 + {v_{{\rm{max}}}}.6 + \dfrac{1}{2}{v_{{\rm{max}}}}.2}}{{12}} = 9 \to {v_{{\rm{max}}}} = 12m/s\)
+ Gia tốc của chất điểm khi chuyển động từ B đến C: \(a = \dfrac{{0 - 12}}{2} = - 6m/s\)
=> Phương trình chuyển động của chất điểm khi đi từ B đến C là: \(x = 96 + 12(t - 10) - 3{(t - 10)^2}\)
Ba vật chuyển động thẳng có đồ thị v - t như hình vẽ:
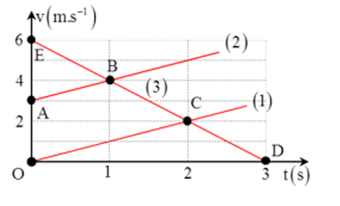
Sau bao nhiêu giây thì vật thứ 3 sẽ dừng lại?
Ta có vật dừng lại khi v = 0
Từ đồ thị, ta có: vật thứ 3 có vận tốc bằng không khi t = 3s
=> Sau 3s thì vật thứ 3 sẽ dừng lại
Một vật chuyển động thẳng chậm dần đều với tốc độ đầu \(3m/s\) và gia tốc \(2m/s^2,\) thời điểm ban đầu ở gốc toạ độ và chuyển động ngược chiều dương của trục toạ độ thì phương trình có dạng.
Ta có: \(\left\{ \begin{array}{l}{x_0} = 0\\{v_0} = - 3m/s\\a = 2m/{s^2}\end{array} \right.\)
Phương trình chuyển động của vật: \(x = - 3t + {t^2}\,\,\left( m \right)\)
Phương trình của một vật chuyển động thẳng là : \(x = 6 + 12t + {t^2}{\mkern 1mu} {\mkern 1mu} \left( {cm;s} \right)\)
a) Xác định gia tốc và vận tốc ban đầu của vật?
b) Viết công thức vận tốc và tính vận tốc của vật sau \(2s\) kể từ thời điểm ban đầu.
Phương trình chuyển động: \(x = 6 + 12t + {t^2}{\mkern 1mu} {\mkern 1mu} \left( {cm;s} \right)\)
a) Vận tốc ban đầu và gia tốc:\(\left\{ {\begin{array}{*{20}{l}}{{v_0} = 12cm/s}\\{a = 2cm/{s^2}}\end{array}} \right.\)
b) Công thức vận tốc : \(v = 12 + 2t\)
Sau \(2\) giây thì vận tốc của vật là : \(v = 12 + 2.2 = 16cm/s\)
Một xe chuyển động nhanh dần đều đi được S = 24m, S2 = 64m trong 2 khoảng thời gian liên tiếp bằng nhau là 4s. Xác định vận tốc ban đầu và gia tốc.
Quãng đường vật đi được trong 2 khoảng thời gian liên tiếp bằng nhau là 4s là :
\(\begin{array}{l}{S_1}\; = {v_{01}}{t_1} + \frac{1}{2}a{t_1}^24.{v_{01}} + 8a = 24{\rm{ }}\left( 1 \right)\\{S_2} = {v_{02}}{t_2} + \frac{1}{2}a{t_2}^2\;4.{v_{01}} + 8a = 64{\rm{ }}\left( 2 \right)\end{array}\)
Mà \({v_{02}} = {v_1} = {v_{01}} + a{t_2}\left( 3 \right)\)
Giải (1), (2), (3) ta được : \({v_{01}} = 1m/s,\;a = 2,5m/{s^2}\)
Hai người đi xe đạp khởi hành cùng một lúc từ 2 địa điểm A và B, đi ngược chiều nhau. Người đi từ A có vận tốc đầu là \(18km/h\) và chuyển động chậm dần đều với gia tốc \(20cm/{s^2}\). Người đi từ B có vận tốc đầu là \(5,4m/s\) và chuyển động nhanh dần đều với gia tốc\(0,2m/{s^2}\). Khoảng cách giữa hai người lúc đầu là \(130m\). Hỏi sau bao lâu 2 người gặp nhau và vị trí gặp nhau?
Chọn gốc tọa độ tại A, chiều dương là chiều từ A đến B, gốc thời gian là lúc hai người bắt đầu khởi hành.
Xe xuất phát từ A có:
\(\left\{ \begin{array}{l}{x_A} = 18km/h = 5m/s\\{a_A} = - 20cm/{s^2} = - 0,2m/{s^2}\\{x_{0A}} = 0\end{array} \right. \Rightarrow {x_A} = 5t - 0,1{t^2}\,\left( m \right)\)
Xe xuất phát từ B có:
\(\left\{ \begin{array}{l}{x_B} = - 5,4m/s\\{a_B} = - 0,2m/{s^2}\\{x_{0B}} = 130m\end{array} \right. \Rightarrow {x_B} = 130 - 5,4t - 0,1{t^2}\,\left( m \right)\)
Hai xe gặp nhau khi:
\(\begin{array}{l}{x_A} = {x_B} \Leftrightarrow 5t - 0,1{t^2} = 130 - 5,4t - 0,1{t^2}\\ \Rightarrow t = 12,5s\end{array}\)
Thay \(t = 12,5s\) vào phương trình của \({x_A}\) ta được:
\({x_A} = 5.12,5 - 0,1.12,{5^2} = 46,875m\)
Một ô tô đang chuyển động với vận tốc 54km/h thì hãm phanh chuyển động chậm dần đều đi được 20m thì vận tốc còn 18km/h. Tính gia tốc của ô tô và quãng đường ô tô đi được từ lúc hãm phanh đến lúc dừng hẳn.
Ta có: \(\left\{ \begin{array}{l}{v_0} = 54km/h = 15m/s\\v = 18km/h = 5m/s\\s = 20m\end{array} \right.\)
Áp dụng công thức liên hệ giữa s, v, a ta có:
\({v^2} - v_0^2 = 2a.s \Rightarrow a = \dfrac{{{v^2} - v_0^2}}{{2s}} = \dfrac{{{5^2} - {{15}^2}}}{{2.20}} = - 5m/{s^2}\)
Khi ô tô dừng hẳn thì: \(v' = 0\)
Áp dụng công thức liên hệ giữa s’, v’, a ta có:
\(v{'^2} - {v^2} = 2a.s' \Rightarrow s' = \dfrac{{v{'^2} - {v^2}}}{{2a}} = \dfrac{{{0^2} - {{15}^2}}}{{2.\left( { - 5} \right)}} = 22,5m\)
Một vật chuyển động có đồ thị vận tốc như hình bên. Công thức vận tốc và công thức đường đi của vật là:
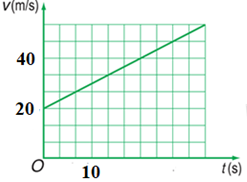
Biễu diễn số liệu như hình vẽ:
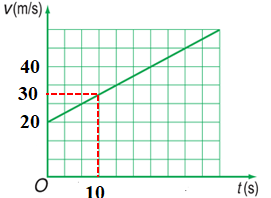
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{t_0} = 0;{v_0} = 20m/s\\{t_1} = 10s;{v_1} = 30m/s\end{array} \right.\)
Gia tốc của vật: \(a = \dfrac{{{v_1} - {v_0}}}{{{t_1} - {t_0}}} = \dfrac{{30 - 20}}{{10}} = 1m/{s^2}\)
Công thức vận tốc và quãng đường:
\(\left\{ \begin{array}{l}v = {v_0} + at = 20 + 1.t\\s = {v_0}t + \dfrac{1}{2}a{t^2} = 20.t + \dfrac{1}{2}.1.{t^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = 20 + t\,\,\left( {m/s} \right)\\s = 20t + \dfrac{{{t^2}}}{2}\,\left( m \right)\end{array} \right.\)

