Một vật chuyển động thẳng có phương trình vận tốc \(v = 2 - 2t\).Tốc độ trung bình của vật sau $4s$ kể từ lúc bắt đầu chuyển động là:
Trả lời bởi giáo viên
Ta để ý rằng sau $1s$ vật đã đổi chiều chuyển động
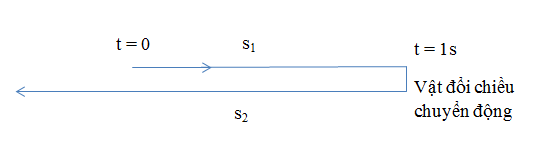
Chọn gốc thời gian là vị trí vật bắt đầu chuyển động, ta có:
Phương trình li độ của vật: \(x = {v_0}t + \dfrac{1}{2}a{t^2} = 2t - {t^2}\)
+ Tại \(t = 0\): \({x_0} = 0\)
+ Tại \(t = 1s\): \({x_1} = 1m\)
+ Tại \(t = 4s\): \({x_4} = - 8m\)
=> Ta suy ra:
+ Quãng đường vật đi được trong giây thứ nhất là: \({s_1} = {x_1} - {x_0} = 1m\)
+ Quãng đường vật đi được từ giây thứ 1 đến giây thứ 4 là: \({s_2} = \left| {{x_4} - {x_1}} \right| = \left| { - 8 - 1} \right| = 9m\)
=> Quãng đường vật đi được sau 4 s: \(s = {s_1} + {s_2} = 1 + 9 = 10m\)
Tốc độ trung bình \({v_{tb}} = \dfrac{s}{t} = \dfrac{{10}}{{1 + 3}} = 2,5m/s\)
Hướng dẫn giải:
+ Xác định quãng đường đi của vật
+ Vận dụng biểu thức tính tốc độ trung bình: \({v_{tb}} = \frac{s}{t}\)

