Trường hợp bằng nhau thứ ba của tam giác

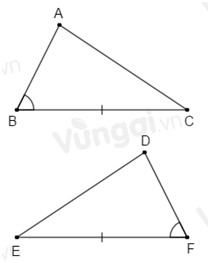
Áp dụng trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc, ta thấy để tam giác $ABC$ và tam giác $DFE$ bằng nhau ta cần thêm một điều kiện là $\widehat C = \widehat E.$

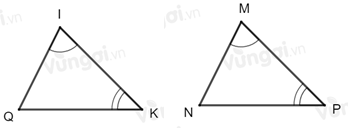
Ta thấy hai tam giác $IQK$ và tam giác $MNP$ có hai yếu tố về góc $\widehat I = \widehat {M,}\widehat K = \widehat P$.

Để tam giác $IQK$ và tam giác $MNP$ bằng nhau theo trường hợp góc – cạnh – góc thì cần thêm điều kiện về cạnh kề hai góc đã cho đó là $IK = MP$.

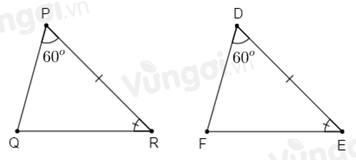
Xét tam giác $PQR$ và tam giác $DFE$ có $\widehat P = \widehat D = {60^ \circ }$, $PR = DE,$ $\widehat R = \widehat E$. Do đó $\Delta PQR = \Delta DFE$ (g.c.g)

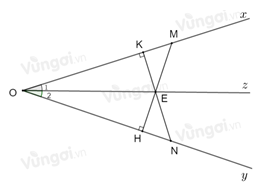
Vì $Oz$ là tia phân giác của $\widehat {xOy}$ nên $\widehat {{O_1}} = \widehat {{O_2}}$

Xét tam giác $OKE$ và tam giác $OHE$ có:

$\widehat {EKO} = \widehat {EHO} = 90^\circ$ (gt)

$OE$ là cạnh chung

$\widehat {{O_2}} = \widehat {{O_1}}$ (cmt)

$\Rightarrow \Delta OKE = \Delta OHE$ (cạnh huyền – góc nhọn)

Do đó $OK = OH$ (hai cạnh tương ứng)

Xét tam giác $OKN$ và tam giác $OHM$ có:

$\widehat {EKO} = \widehat {EHO} = 90^\circ$ (gt)

$OK = OH$  (cmt)

$\widehat {MON}$ chung

$\Rightarrow \Delta OKN = \Delta OHM\,(g.c.g)$  

Do đó $KN = HM$ (hai cạnh tương ứng).

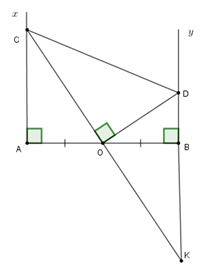
Kéo dài $OC$ cắt $BD$ tại $K.$ Ta có $OD \bot OC \Rightarrow OD \bot CK \Rightarrow \widehat {COD} = \widehat {KOD} = 90^\circ$; $AB \bot DK \Rightarrow \widehat {OBD} = \widehat {OBK} = 90^\circ .$

Xét tam giác $AOC$ và tam giác $BOK$ có:

+ $\widehat {OAC} = \widehat {OBK} = 90^\circ$

+ $OA = OB\,$ ($O$ là trung điểm của $AB$ )

+ $\widehat {AOC} = \widehat {BOK}$ (hai góc đối đỉnh)

Suy ra $\Delta AOC = \Delta BOK\left( {g.c.g} \right)$ $\Rightarrow OC = OK$ (hai cạnh tương ứng); $AC = BK$ (hai cạnh tương ứng)

Xét tam giác $DOC$ và tam giác $DOK$ có:

+ $OC = OK$ (cmt)

+ $\widehat {DOC} = \widehat {DOK} = 90^\circ$ (cmt)

+ $OD$ là cạnh chung

Suy ra $\Delta DOC = \Delta DOK\left( {c.g.c} \right)$ $\Rightarrow CD = DK$ (hai cạnh tương ứng)

Ta có: $DK = DB + BK$ mà $AC = BK$ (cmt) và $CD = DK$ (cmt) nên $CD = AC + BD = 5 + 2 = 7(cm)$.

 Vậy $CD = 7(cm).$

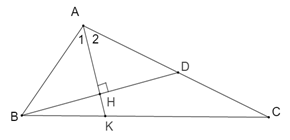
Vì $AK$ là tia phân giác của $\widehat {BAC}$ nên $\widehat {{A_1}} = \widehat {{A_2}}$

Theo giả thiết ta có: $BH \bot AK \Rightarrow BD \bot AK \Rightarrow \widehat {AHB} = \widehat {AHD} = 90^\circ$

Xét tam giác $AHB$ và tam giác $AHD$ có:

+ $\widehat {{A_1}} = \widehat {{A_2}}$ (cmt)

+ $AH$ là cạnh chung

+ $\widehat {AHB} = \widehat {AHD} = 90^\circ$

Nên $\Delta {\rm A}{\rm H}{\rm B} = \Delta {\rm A}{\rm H}{\rm{D}}\left( {g.c.g} \right)$ $\Rightarrow HB = HD;AB = AD$ (hai cạnh tương ứng) ; $\widehat {ABH} = \widehat {ADH}$ (hai góc tương ứng)

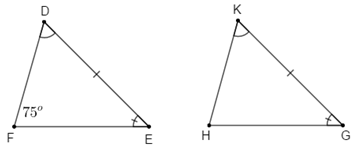
Xét tam giác $DEF$ và tam giác $KGH$ có $\widehat D = \widehat K$, $\widehat E = \widehat G$, $DE = KG$

Do đó $\Delta DEF = \Delta KGH\,(g.c.g)$

Do đó $\widehat H = \widehat F = {75^0}$ (hai góc tương ứng).

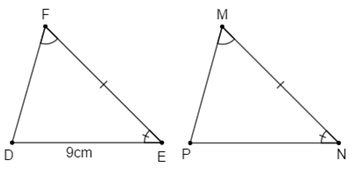
Xét tam giác $MNP$  và tam giác $FED$ có $MN = EF,$ $\widehat M = \widehat F$, $\widehat N = \widehat E$.

Do đó $\Delta MNP = \Delta FED\,\left( {g.c.g} \right)$.

Do đó $NP = ED = 9cm$ (hai cạnh tương ứng).

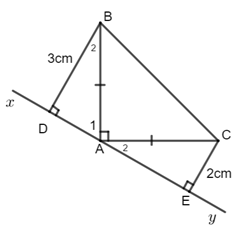
Ta có: ${\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)$.

Mà ${\widehat A_1} + {\widehat B_2} = {90^0}$ vì tam giác $ABD$  vuông tại $D.$

$\Rightarrow {\widehat B_2} = {\widehat A_2}$  (cùng phụ với ${\widehat A_1}$).

Xét tam giác $BDA$ và tam giác $AEC$ có:

$\widehat D = \widehat E = {90^0}$; $AB = AC$ (gt) và ${\widehat B_2} = {\widehat A_2}$ (cmt)

$\Rightarrow \Delta BDA = \Delta AEC$ (cạnh huyền – góc nhọn)

Suy ra $BD = AE$ (hai cạnh tương ứng), $CE = AD$ (hai cạnh tương ứng).

Do đó $DE = AD + AE = CE + BD = 2 + 3 = 5cm$

Áp dụng trường hợp bằng nhau thứ ba của  tam giác ta thấy cần thêm điều kiện về góc kề cạnh đó là  $\widehat C = \widehat M.$

Ta thấy hai tam giác $ABC$  và tam giác $MNP$ có hai yếu tố về góc  $\widehat A = \widehat {M,}\widehat B = \widehat N$.

Để tam giác $ABC$  và tam giác $MNP$ bằng nhau theo trường hợp góc – cạnh – góc thì cần thêm điều kiện về cạnh kề hai góc đã cho đó là $AB = MN.$

Xét tam giác $ABC$  và tam giác $MNP$  có  $\widehat B = \widehat N = {90^ \circ }$, $AC = MP$, $\widehat C = \widehat M$ , do đó  $\Delta ABC = \Delta PNM$ (cạnh huyền – góc nhọn) 

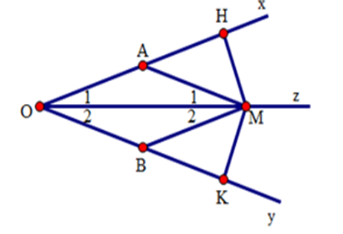
Ta có:

$\widehat {{M_1}} = \widehat {{O_2}}$ (hai góc so le trong)

$\widehat {{M_2}} = \widehat {{O_1}}$ (hai góc so le trong)

$\widehat {{O_2}} = \widehat {{O_1}}$(do $Oz$ là tia phân giác của góc $xOy$)

Do đó $\widehat {{M_2}} = \widehat {{M_1}}$

Xét tam giác $AOM$  và tam giác $BOM$  có:

 $\widehat {{M_2}} = \widehat {{M_1}}$(cmt)

 $OM$  là cạnh chung

  $\widehat {{O_2}} = \widehat {{O_1}}$(cmt)

$\Rightarrow \Delta AOM = \Delta BOM (g.c.g)$

Do đó $OA = OB;MA = MB$ (các cặp cạnh tương ứng).

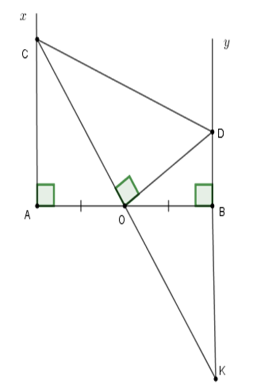
Kéo dài $OC$ cắt $BD$ tại $K.$ Khi đó $OD \bot OC \Rightarrow OD \bot CK \Rightarrow \widehat {COD} = \widehat {KOD} = 90^\circ$  ; $AB \bot DK \Rightarrow \widehat {OBD} = \widehat {OBK} = 90^\circ .$

Xét tam giác $AOC$ và tam giác $BOK$ có

+ $\widehat {OAC} = \widehat {OBK} = 90^\circ$

+ $OA = OB\,$ ($O$ là trung điểm của $AB$)

+ $\widehat {AOC} = \widehat {BOK}$ (hai góc đối đỉnh)

Suy ra $\Delta AOC = \Delta BOK\left( {g - c - g} \right)$ $\Rightarrow OC = OK$ (hai cạnh tương ứng); $AC = BK$ (hai cạnh tương ứng)

Xét tam giác $DOC$ và tam giác $DOK$ có

+ $OC = OK$ (cmt)

+ $\widehat {DOC} = \widehat {DOK} = 90^\circ$

+ Cạnh $OD$ chung,

Suy ra $\Delta DOC = \Delta DOK\left( {g - c - g} \right)$ $\Rightarrow CD = DK$ (hai cạnh tương ứng)

Ta có $DK = DB + BK$ mà $AC = BK$(cmt) và $CD = DK$ (cmt) nên $CD = AC + BD.$

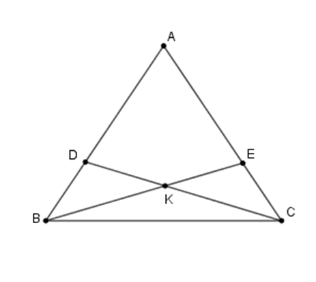
Xét tam giác $ABE$ và tam giác $ACD$ có

+ $AE = AD\left( {gt} \right)$

 + Góc $A$ chung

+ $AB = AC\left( {gt} \right)$

Suy ra $\Delta ABE = \Delta ACD\left( {c - g - c} \right)$ $\Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}$ (hai góc tương ứng) và $BE = CD$ (hai cạnh tương ứng) nên A đúng.

Lại có $\widehat {ADC} + \widehat {BDC} = 180^\circ$; $\widehat {AEB} + \widehat {BEC} = 180^\circ$ (hai góc kề bù) mà $\widehat {ADC} = \widehat {AEB}$ (cmt)

Suy ra $\widehat {BDC} = \widehat {BEC}.$

Lại có $AB = AC;\,AD = AE\left( {gt} \right)$ $\Rightarrow AB - AD = AC - AE \Rightarrow BD = EC$ nên C đúng.

Xét tam giác $KBD$ và tam giác $KCE$ có

+ $\widehat {ABE} = \widehat {ACD}\,\left( {cmt} \right)$

+ $BD = EC\,\left( {cmt} \right)$

+  $\widehat {BDC} = \widehat {BEC}\,\left( {cmt} \right)$

Nên $\Delta KBD = \Delta KCE\left( {g - c - g} \right)$ $\Rightarrow KB = KC;\,KD = KE$ (hai cạnh tương ứng)  nên B đúng, D sai.

Xét tam giác $DEF$  và tam giác $HKG$  có $\widehat D = \widehat H$, $\widehat E = \widehat K$, $DE = HK,$ do đó $\Delta DEF = \Delta HKG$(g.c.g).

Do đó $\widehat G = \widehat F = {80^0}$ (hai góc tương ứng).

Xét tam giác $ABC$  và tam giác $DEF$ có $AB = DE,$ $\widehat B = \widehat E$ , $\widehat A = \widehat D$ , do đó $\Delta ABC = \Delta DEF\,\left( {g - c - g} \right)$.

Do đó $DF = AC = 6cm$ (hai cạnh tương ứng).

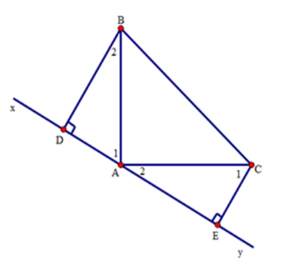
Ta có: ${\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)$

Mà ${\widehat A_1} + {\widehat B_2} = {90^0}$ vì tam giác $ABD$  vuông tại $D.$

$\Rightarrow {\widehat B_2} = {\widehat A_2}$  (cùng phụ với ${\widehat A_1}$).

Lại có ${\widehat A_2} + {\widehat C_1} = {90^0}$ vì tam giác $ACE$  vuông tại $E$

$\Rightarrow {\widehat A_1} = {\widehat C_1}$ (cùng phụ với ${\widehat A_2}$).

Xét hai tam giác vuông $BDA$  và $AEC$  có:

$\widehat D = \widehat E = {90^0}$; $AB = AC$ (gt) và $\widehat {{A_1}} = \widehat {{C_1}}$ (cmt)

$\Rightarrow \Delta BA{\rm{D}} = \Delta ACE$ (cạnh huyền – góc nhọn)

Suy ra $BD = AE$ (hai cạnh tương ứng), $CE = AD$ (hai cạnh tương ứng).

Do đó $DE = AD + AE = CE + BD.$

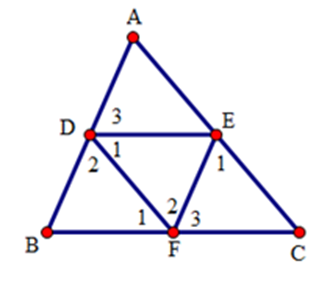
Xét tam giác $DEF$  và tam giác $FBD$  có:

$\widehat {{D_1}} = \widehat {{F_1}}$ (hai góc so le trong).

$DF$ là cạnh chung

$\widehat {{F_2}} = \widehat {{D_2}}$ (hai góc so le trong).

Vậy $\Delta DEF = \Delta FBD\,\,\,(g.c.g)$

Suy ra $EF = BD$ (hai cạnh tương ứng)

 Mà $AD = BD$ nên $EF = AD$

Ta có : $\widehat {{F_3}} = \widehat B$ (hai góc đồng vị); $\widehat {{D_3}} = \widehat B$ (hai góc đồng vị)

 $\Rightarrow \widehat {{D_3}} = \widehat {{F_3}}\left( { = \widehat B} \right).$.

Xét tam giác $ADE$ và tam giác $EFC$  có:

$\widehat {{D_3}} = \widehat {{F_3}}$(cmt)

$\widehat A = \widehat {{E_1}}$(hai góc đồng vị)

$AD = EF\left( {cmt} \right)$

 $\Rightarrow \Delta ADE = \Delta EFC\,\,\,(g.c.g).$  (1)

Tương tự ta chứng minh được $\Delta EFC = \Delta DBF\,\,\,(g.c.g)$     (2)

Từ (1) và (2) suy ra $\Delta ADE = \Delta EFC = \Delta DBF$                      (3)

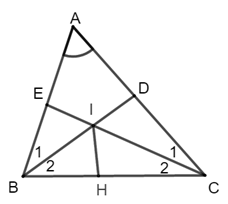
Vì $BD$ là tia phân giác của $\widehat {ABC}$ nên $\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}\widehat {ABC}$

Vì $CE$ là tia phân giác của $\widehat {ACB}$ nên $\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}\widehat {ACB}$

Xét $\Delta ABC$ có: $\widehat A + \widehat {ABC} + \widehat {ACB} = 180^\circ$ (tổng ba góc của một tam giác bằng $180^\circ$)

Mà $\widehat A = 60^\circ$ nên $\widehat {ABC} + \widehat {ACB} = 180^\circ  - \widehat A = 180^\circ  - 60^\circ  = 120^\circ$

Ta lại có: $\widehat {{B_2}} + \widehat {{C_2}} = \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}(\widehat {ABC} + \widehat {ACB}) = \dfrac{1}{2}.120^\circ  = 60^\circ$

Xét $\Delta BIC$ có $\widehat {BIC} + \widehat {{B_2}} + \widehat {{C_2}} = 180^\circ$ (tổng ba góc của một tam giác bằng $180^\circ$)

Mà $\widehat {{B_2}} + \widehat {{C_2}} = 60^\circ$ nên $\widehat {BIC} = 180^\circ  - (\widehat {{B_2}} + \widehat {{C_2}}) = 180^\circ  - 60^\circ  = 120^\circ$

Mặt khác: $\widehat {BIC} + \widehat {BIE} = 180^\circ$ (hai góc kề bù) $\Rightarrow \widehat {BIE} = 180^\circ  - \widehat {BIC} = 180^\circ  - 120^\circ  = 60^\circ$

Khi đó $\widehat {CID} = \widehat {BIE} = 60^\circ$ (hai góc đối đỉnh)  $(1)$

Kẻ tia phân giác của $\widehat {BIC}$ cắt $BC$ tại $H$

Suy ra $\widehat {BIH} = \widehat {HIC} = \dfrac{1}{2}.\widehat {BIC} = \dfrac{1}{2}.120^\circ  = 60^\circ$$(2)$

Từ $(1)$ và $(2)$ suy ra $\widehat {CID} = \widehat {BIE} = \widehat {BIH} = \widehat {HIC}$

Xét tam giác $BIE$ và tam giác $BIH$ có:

$\widehat {{B_1}} = \widehat {{B_2}}$ (cmt)

$BI$ là cạnh chung

$\widehat {BIE} = \widehat {BIH}$ (cmt)

$\Rightarrow \Delta BIE = \Delta BIH \,(g.c.g) \Rightarrow IE = IH$ (hai cạnh tương ứng) $(3)$

Xét tam giác $CID$ và tam giác $CIH$ có:

$\widehat {{C_1}} = \widehat {{C_2}}$ (cmt)

$CI$ là cạnh chung

$\widehat {CID} = \widehat {HIC}$ (cmt)

$\Rightarrow \Delta CID = \Delta CIH \,(g.c.g) \Rightarrow ID = IH$ (hai cạnh tương ứng) $(4)$

Từ $(3)$ và $(4)$ suy ra $ID = IE = 2cm$