Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = AC.\) Qua \(A\) kẻ đường thẳng \(xy\) sao cho \(B,C\) nằm cùng phía với \(xy.\) Kẻ \(BD\) và \(CE\) vuông góc với \(xy.\) Tính \(DE\) biết \(BD = 3\,cm;CE = 2\,cm.\)
Trả lời bởi giáo viên
Đáp án đúng: a
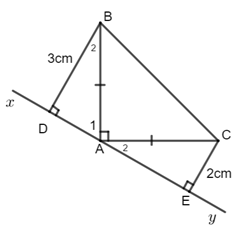
Ta có: \({\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)\).
Mà \({\widehat A_1} + {\widehat B_2} = {90^0}\) vì tam giác \(ABD\) vuông tại \(D.\)
\( \Rightarrow {\widehat B_2} = {\widehat A_2}\) (cùng phụ với \({\widehat A_1}\)).
Xét tam giác \(BDA\) và tam giác \(AEC\) có:
\(\widehat D = \widehat E = {90^0}\); \(AB = AC\) (gt) và \({\widehat B_2} = {\widehat A_2}\) (cmt)
\( \Rightarrow \Delta BDA = \Delta AEC\) (cạnh huyền – góc nhọn)
Suy ra \(BD = AE\) (hai cạnh tương ứng), \(CE = AD\) (hai cạnh tương ứng).
Do đó \(DE = AD + AE = CE + BD = 2 + 3 = 5cm\)
Hướng dẫn giải:
+ Áp dụng hệ quả của trường hợp bằng nhau thứ ba của tam giác: “Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau” để chứng minh hai tam giác \(BDA\) và \(AEC\) bằng nhau.
+ Từ đó suy ra các cạnh tương ứng bằng nhau và tính \(DE\).
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
