Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(AB < AC.\) Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Từ \(B\) kẻ đường thẳng vuông góc với \(AK\) tại \(H\) cắt \(AC\) ở \(D.\) Chọn câu sai.
Trả lời bởi giáo viên
Đáp án đúng: b
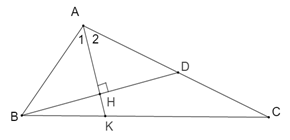
Vì \(AK\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {{A_1}} = \widehat {{A_2}}\)
Theo giả thiết ta có: \(BH \bot AK \Rightarrow BD \bot AK \Rightarrow \widehat {AHB} = \widehat {AHD} = 90^\circ \)
Xét tam giác \(AHB\) và tam giác \(AHD\) có:
+ \(\widehat {{A_1}} = \widehat {{A_2}}\) (cmt)
+ \(AH\) là cạnh chung
+ \(\widehat {AHB} = \widehat {AHD} = 90^\circ \)
Nên \(\Delta {\rm A}{\rm H}{\rm B} = \Delta {\rm A}{\rm H}{\rm{D}}\left( {g.c.g} \right)\) \( \Rightarrow HB = HD;AB = AD\) (hai cạnh tương ứng) ; \(\widehat {ABH} = \widehat {ADH}\) (hai góc tương ứng)
Hướng dẫn giải:
+ Áp dụng trường hợp bằng nhau thứ ba của tam giác: “Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau” để chứng minh \(\Delta {\rm A}{\rm H}{\rm B} = \Delta AHD\), từ đó suy ra các cạnh bằng nhau, các góc bằng nhau.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
