Câu hỏi:
2 năm trước
Cho đoạn thẳng \(AB,O\) là trung điểm của \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB\) vẽ các tia \(Ax;By\) vuông góc với \(AB.\) Gọi \(C\) là một điểm thuộc tia \(Ax.\) Đường vuông góc với \(OC\) tại ${\rm{O}}$ cắt tia \(By\) ở \(D.\) Khi đó
Trả lời bởi giáo viên
Đáp án đúng: d
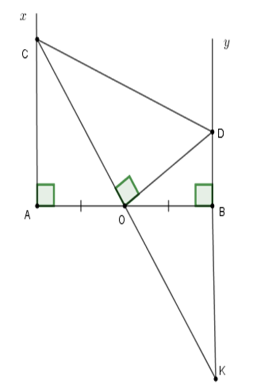
Kéo dài \(OC\) cắt \(BD\) tại \(K.\) Khi đó \(OD \bot OC \Rightarrow OD \bot CK \Rightarrow \widehat {COD} = \widehat {KOD} = 90^\circ \) ; \(AB \bot DK \Rightarrow \widehat {OBD} = \widehat {OBK} = 90^\circ .\)
Xét tam giác \(AOC\) và tam giác \(BOK\) có
+ \(\widehat {OAC} = \widehat {OBK} = 90^\circ \)
+ \(OA = OB\,\) (\(O\) là trung điểm của \(AB\))
+ \(\widehat {AOC} = \widehat {BOK}\) (hai góc đối đỉnh)
Suy ra \(\Delta AOC = \Delta BOK\left( {g - c - g} \right)\) \( \Rightarrow OC = OK\) (hai cạnh tương ứng); \(AC = BK\) (hai cạnh tương ứng)
Xét tam giác \(DOC\) và tam giác \(DOK\) có
+ \(OC = OK\) (cmt)
+ \(\widehat {DOC} = \widehat {DOK} = 90^\circ \)
+ Cạnh \(OD\) chung,
Suy ra \(\Delta DOC = \Delta DOK\left( {g - c - g} \right)\) \( \Rightarrow CD = DK\) (hai cạnh tương ứng)
Ta có $DK = DB + BK$ mà \(AC = BK\)(cmt) và \(CD = DK\) (cmt) nên \(CD = AC + BD.\)
Hướng dẫn giải:
+ Kéo dài \(OC\) cắt \(BD\) tại \(K.\)
+ Chứng minh \(AC = BK\) dựa vào hai tam giác bằng nhau \(AOC\) và \(BOK.\)
+ Chứng minh hai tam giác bằng nhau \(COD\) và \(KOD\) từ đó suy mối quan hệ giữa các đoạn thẳng.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
