Cho tam giác \(ABC\) có \(AB = AC.\) Trên các cạnh \(AB\) và \(AC\) lấy các điểm \(D,E\) sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của \(BE\) và \(CD\). Chọn câu sai.

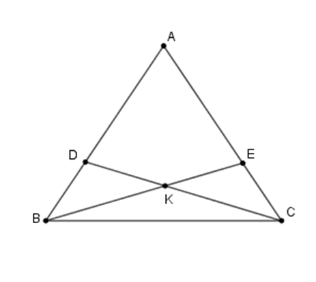
Cho tam giác \(ABC\) và tam giác \(DEF\) có $\widehat B = \widehat F,BC = FE$. Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(DFE\) bằng nhau theo trường hợp góc – cạnh – góc?

Cho tam giác \(IKQ\) và tam giác \(MNP\) có \(\widehat I = \widehat {M,}\widehat K = \widehat P\). Cần thêm điều kiện gì để tam giác \(IQK\) và tam giác \(MNP\)  bằng nhau theo trường hợp góc – cạnh – góc:

Cho tam giác \(PQR\) và tam giác \(DEF\) có \(\widehat P = \widehat D = {60^ \circ }\), \(PR = DE,\) \(\widehat R = \widehat E\). Phát biểu nào trong các phát biểu sau đây là đúng:

Cho góc \(xOy\) có tia phân giác \(Oz.\) Trên \(Oz\) lấy điểm \(E,\) vẽ đường thẳng qua \(E\) vuông góc với \(Ox\) tại \(K,\) cắt \(Oy\) tại \(N.\) Vẽ đường thẳng qua \(E\) vuông góc với \(Oy\) tại \(H\) cắt \(Ox\) tại \(M.\) Chọn câu đúng.

Cho đoạn thẳng \(AB,O\) là trung điểm của \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB\) vẽ các tia \(Ax;By\) vuông góc với \(AB.\) Gọi \(C\) là một điểm thuộc tia \(Ax.\) Đường vuông góc với \(OC\) tại \({\rm{O}}\) cắt tia \(By\) ở \(D.\) Tính \(DC\) biết \(AC = 5\,cm;\,BD = 2\,cm.\)

Cho tam giác \(ABC\) có \(AB < AC.\) Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Từ \(B\) kẻ đường thẳng vuông góc với \(AK\) tại \(H\) cắt \(AC\) ở \(D.\) Chọn câu sai.

Cho tam giác \(DEF\) và tam giác \(HKG\) có \(\widehat D = \widehat K\), \(\widehat E = \widehat G\), \(DE = KG.\) Biết \(\widehat F = {75^0}\). Số đo góc \(H\) là: