Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $A$ có $AB = AC.$ Qua $A$ kẻ đường thẳng $xy$ sao cho $B,C$ nằm cùng phía với $xy.$ Kẻ $BD$ và $CE$ vuông góc với $xy.$ Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: a
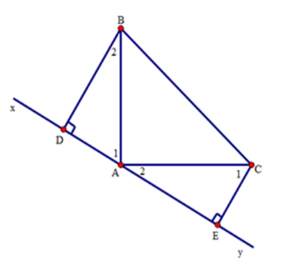
Ta có: \({\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)\)
Mà ${\widehat A_1} + {\widehat B_2} = {90^0}$ vì tam giác $ABD$ vuông tại $D.$
\( \Rightarrow {\widehat B_2} = {\widehat A_2}\) (cùng phụ với \({\widehat A_1}\)).
Lại có \({\widehat A_2} + {\widehat C_1} = {90^0}\) vì tam giác $ACE$ vuông tại $E$
\( \Rightarrow {\widehat A_1} = {\widehat C_1}\) (cùng phụ với \({\widehat A_2}\)).
Xét hai tam giác vuông $BDA$ và $AEC$ có:
\(\widehat D = \widehat E = {90^0}\); \(AB = AC\) (gt) và \(\widehat {{A_1}} = \widehat {{C_1}}\) (cmt)
\( \Rightarrow \Delta BA{\rm{D}} = \Delta ACE\) (cạnh huyền – góc nhọn)
Suy ra $BD = AE$ (hai cạnh tương ứng), $CE = AD$ (hai cạnh tương ứng).
Do đó $DE = AD + AE = CE + BD.$
Hướng dẫn giải:
+ Dựa vào hệ quả của trường hợp bằng nhau thứ ba của tam giác để chứng minh các cặp tam giác bằng nhau
+ Từ các cặp cạnh tương ứng bằng nhau ta lập luận để suy ra mối quan hệ đúng.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
