Câu hỏi:
2 năm trước
Cho tam giác $ABC,D$ là trung điểm của $AB.$ Đường thẳng qua $D$ và song song với $BC$ cắt $AC$ ở $E,$ đường thẳng qua $E$ và song song với $AB$ cắt $BC$ ở $F.$ Khi đó
Trả lời bởi giáo viên
Đáp án đúng: d
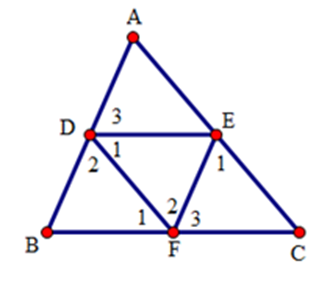
Xét tam giác $DEF$ và tam giác $FBD$ có:
\(\widehat {{D_1}} = \widehat {{F_1}}\) (hai góc so le trong).
$DF$ là cạnh chung
\(\widehat {{F_2}} = \widehat {{D_2}}\) (hai góc so le trong).
Vậy \(\Delta DEF = \Delta FBD\,\,\,(g.c.g)\)
Suy ra $EF = BD$ (hai cạnh tương ứng)
Mà $AD = BD$ nên $EF = AD$
Ta có : \(\widehat {{F_3}} = \widehat B\) (hai góc đồng vị); \(\widehat {{D_3}} = \widehat B\) (hai góc đồng vị)
\( \Rightarrow \widehat {{D_3}} = \widehat {{F_3}}\left( { = \widehat B} \right).\).
Xét tam giác $ADE$ và tam giác $EFC$ có:
\(\widehat {{D_3}} = \widehat {{F_3}}\)(cmt)
\(\widehat A = \widehat {{E_1}}\)(hai góc đồng vị)
$AD = EF\left( {cmt} \right)$
\( \Rightarrow \Delta ADE = \Delta EFC\,\,\,(g.c.g).\) (1)
Tương tự ta chứng minh được \(\Delta EFC = \Delta DBF\,\,\,(g.c.g)\) (2)
Từ (1) và (2) suy ra \(\Delta ADE = \Delta EFC = \Delta DBF\) (3)
Hướng dẫn giải:
+ Từ tính chất của hai đường song song suy ra các cặp góc bằng nhau, từ đó dựa vào trường hợp bằng nhau thứ ba của tam giác để chứng minh các tam giác bằng nhau
+ Từ các cặp cạnh bằng nhau ta tìm mối liên hệ giữa chúng để suy ra điều phải chứng minh
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
