Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là \(a,\,\,2a,\,\,3a\) có thể tích lớn nhất bằng
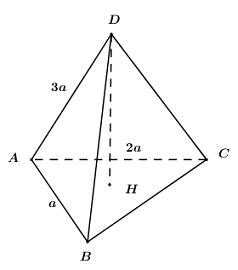
Giả sử khối chóp \(ABCD\) có \(AB = a,\,\,AC = 2a,\,\,AD = 3a\).
Gọi \(H\) là hình chiếu vuông góc của \(D\) lên \(\left( {ABC} \right)\), khi đó ta có: \(DH \bot \left( {ABC} \right)\) và \(DH \le AD\).
Ta có: \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC \le \dfrac{1}{2}AB.AC\).
Vây \({V_{ABCD}} = \dfrac{1}{3}DH.{S_{\Delta ABC}} \le \dfrac{1}{3}AD.\dfrac{1}{2}AB.AC = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.a.2a.3a = {a^3}\).
Dấu “=” xảy ra \( \Leftrightarrow AD \bot \left( {ABC} \right),\,\,AB \bot AC\) hay \(AB,\,\,AC,\,\,AD\) đôi một vuông góc.
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, \(AB = 2a,\)\(AD = a\)\(\left( {a > 0} \right)\). M là trung điểm của AB, tam giác SMC vuông tại S, \(\left( {SMC} \right) \bot \left( {ABCD} \right),\)\(SM\) tạo với đáy góc \(60^\circ \). Thể tích của khối chóp S.ABCD là:
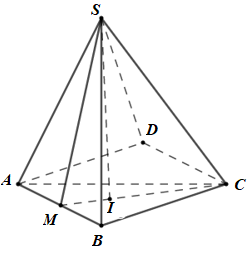
Trong \(\left( {SMC} \right)\) kẻ \(SI \bot MC\,\,\left( {I \in MC} \right)\) ta có: \(\left\{ \begin{array}{l}\left( {SMC} \right) \bot \left( {ABCD} \right) = MC\\SI \subset \left( {SMC} \right),\,\,SI \bot MC\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\).
\( \Rightarrow IM\) là hình chiếu của \(SM\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \angle \left( {SM;\left( {ABCD} \right)} \right) = \angle \left( {SM;IM} \right) = \angle SMI = \angle SMC = {60^0}\).
Áp dụng định lí Pytago trong tam giác BMC vuông tại B :
\(BM = \dfrac{{AB}}{2} = a;\,\,BC = a\)\( \Rightarrow MC = \sqrt {B{C^2} + B{M^2}} = a\sqrt 2 \).
Xét tam giác SMC vuông tại \(S\) có \(\angle SMC = {60^0};\,\,MC = a\sqrt 2 \) \( \Rightarrow SM = MC.\cos {60^0} = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác SMI vuông tại \(I\) có \(\angle SMI = {60^0};\,\,SM = \dfrac{{a\sqrt 2 }}{2}\) \( \Rightarrow SI = SM.sin{60^0} = \dfrac{{a\sqrt 2 }}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{4}\).
Vậy thể tích khối chóp là \(V = \dfrac{1}{3}SI.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{4}.2{a^2} = \dfrac{{{a^3}\sqrt 6 }}{6}.\)
Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = BC\sqrt 5 \), \(AC = 2BC\sqrt 2 \), hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(O\) của cạnh \(AC\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng 2. Mặt phẳng \(\left( {SBC} \right)\) hợp với mặt phẳng \(\left( {ABC} \right)\) một góc \(\alpha \) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt a }}{b}\), trong đó \(a,\,\,b \in {\mathbb{N}^*}\), \(a\) là số nguyên tố. Tổng \(a + b\) bằng:
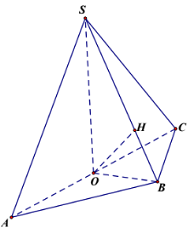
Gọi \(H\) là hình chiếu của \(O\) lên \(SB\).
Ta có: \(OB = \sqrt {\dfrac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC\), \(OC = \dfrac{1}{2}AC = BC\sqrt 2 \). Suy ra \(OB \bot BC\).
Dễ thấy \(\angle SBO = \alpha \) và \(OH = d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\).
Suy ra \(SO = \dfrac{{OH}}{{\cos \alpha }} = \dfrac{1}{{\cos \alpha }}\), \(OB = \dfrac{{OH}}{{\sin \alpha }} = \dfrac{1}{{\sin \alpha }}\).
\( \Rightarrow BC = OB = \dfrac{1}{{\sin \alpha }}\).
Thể tích khối chóp \(S.ABC\) là:
\(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}} = \dfrac{1}{3}SO.2{S_{OBC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{{\cos \alpha }}.{\left( {\dfrac{1}{{\sin \alpha }}} \right)^2} = \dfrac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}\end{array}\)
Áp dụng bất đẳng thức Cô-si ta có:
\(\begin{array}{l}1 = \dfrac{1}{2}{\sin ^2}\alpha + \dfrac{1}{2}{\sin ^2}\alpha + {\cos ^2}\alpha \ge 3.\sqrt[3]{{\dfrac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}\\ \Leftrightarrow \dfrac{1}{{27}} \ge \dfrac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \dfrac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \dfrac{{3\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABC}} \ge \dfrac{{\sqrt 3 }}{2}\end{array}\)
Vậy \(\min {V_{S.ABC}} = \dfrac{{\sqrt 3 }}{2}\). Dấu “=” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = \dfrac{1}{2}{\sin ^2}\alpha = \dfrac{1}{3} \Leftrightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{3}\).
\( \Rightarrow a = 3,\,\,b = 2\).
Vậy \(a + b = 3 + 2 = 5\).
Cho hình chóp S.ABC có \(SA = SB = SC = a\sqrt {3},\) \(AB = AC = 2a,BC = 3a\). Thể tích khối chóp S.ABC bằng:
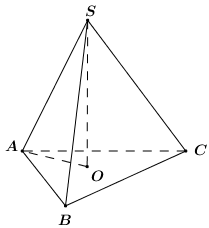
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
Vì $SA=SB=SC$ nên $S$ là điểm cách đều 3 điểm $A, B, C$.
Khi đó $S$ thuộc đường thẳng vuông góc với mặt phẳng $(ABC)$ tại $O$.
Hay $SO$ vuông góc với $(ABC)$
Gọi bán kính đường tròn ngoại tiếp tam giác $(ABC)$ là $R$$ \Rightarrow R=OA$
Ta có \(\dfrac{a}{{\sin A}} = 2R \Rightarrow 2R = \dfrac{{BC}}{{\sin BAC}}\)
Tam giác ABC có \(AB = AC = 2a;BC = 3a\)
\( \Rightarrow \cos BAC = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = - \dfrac{1}{8} \Rightarrow \sin BAC = \dfrac{{3\sqrt 7 }}{8}\)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC.\sin BAC = \dfrac{{{a^2}.3\sqrt 7 }}{4}\)
Khi đó \(R = \dfrac{{BC}}{{2\sin BAC}} = \dfrac{{3a}}{{2.\dfrac{{3\sqrt 7 }}{8}}} = \dfrac{{4a\sqrt 7 }}{7}\)
Chiều cao hình chóp là \(h =SO= \sqrt {S{A^2} - {R^2}} = \dfrac{{a\sqrt {35} }}{7}\)
Khi đó thể tích hình chóp là \(V = \dfrac{1}{3}h.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt {35} }}{7}.\dfrac{{3\sqrt 7 }}{4}{a^2} = \dfrac{{{a^3}\sqrt 5 }}{4}\).
Cho khối chóp S.ABCD có thể tích bằng \(4{a^3}\), đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng \({a^2}\). Tính khoảng cách từ M tới mặt phẳng \(\left( {SAB} \right)\).
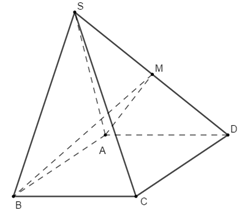
Vì M là trung điểm của SD nên \(\frac{{{V_{SABM}}}}{{{V_{SABD}}}} = \frac{{SM}}{{SD}} = \frac{1}{2}\)
Mà \(\frac{{{V_{SABD}}}}{{{V_{SABCD}}}} = \frac{1}{2} \Rightarrow {V_{SABD}} = \frac{1}{2}.4{a^3} = 2{a^3}\)
\( \Rightarrow {V_{SABM}} = {a^3} = \frac{1}{3}.d\left( {M;\left( {SAB} \right)} \right).{S_{SAB}} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \frac{{3{a^3}}}{{{a^2}}} = 3a\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng
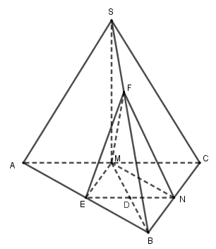
Gọi D là giao điểm của MB và EN thì D là trung điểm của MB.
Ta có: \({V_{MNEF}} = {V_{M.NEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {M,\left( {NEF} \right)} \right)\)
Do D là trung điểm của MB và MB cắt (EFN) tại D nên \(d\left( {M,\left( {NEF} \right)} \right) = d\left( {B,\left( {NEF} \right)} \right)\)
\( \Rightarrow {V_{MNEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {B,\left( {NEF} \right)} \right)\)\( = {V_{B.NEF}}\)
Mà \(\dfrac{{{V_{B.NEF}}}}{{{V_{B.CAS}}}} = \dfrac{{BN}}{{BC}}.\dfrac{{BE}}{{BA}}.\dfrac{{BF}}{{BS}}\)\( = \dfrac{1}{2}.\dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{6}\)
\( \Rightarrow {V_{B.NEF}} = \dfrac{1}{6}{V_{B.CAS}} = \dfrac{1}{6}{V_{S.ABC}}\)
Vì SA=SB=SC nên \(S\) nằm trên trục đường tròn ngoại tiếp tam giác ABC.
Mà ABC vuông cân nên M là tâm đường tròn ngoại tiếp tam giác. Do đó \(SM \bot \left( {ABC} \right)\).
Diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.4.4 = 8\)
Tam giác ABC vuông cân tại B nên
\(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} \\ = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \\ \Rightarrow AM = \dfrac{1}{2}AC = \dfrac{1}{2}.4\sqrt 2 = 2\sqrt 2 \end{array}\)
Tam giác \(SMA\) vuông tại M nên theo Pitago ta có: \(SM = \sqrt {S{A^2} - A{M^2}} \)\( = \sqrt {{{12}^2} - {{\left( {2\sqrt 2 } \right)}^2}} = 2\sqrt {34} \)
Thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SM\)\( = \dfrac{1}{3}.8.2\sqrt {34} \) $ = \dfrac{{16\sqrt {34} }}{3}$
Thể tích khối tứ diện MNEF là: \({V_{MNEF}} = \dfrac{1}{6}.{V_{S.ABC}}\)\( = \dfrac{1}{6}.\dfrac{{16\sqrt {34} }}{3} = \dfrac{{8\sqrt {34} }}{9}\)
Cho hình tứ diện đều \(ABCD\) có độ dài các cạnh bằng \(1\). Gọi \(A',\,\,B',\,\,C',\,\,D'\) lần lượt là điểm đối xứng của \(A,\,\,B,\,\,C,\,\,D\) qua các mặt phẳng \(\left( {BCD} \right),\,\,\left( {ACD} \right),\,\,\left( {ABD} \right),\,\,\left( {ABC} \right)\). Tính thể tích của khối tứ diện \(A'B'C'D'\).
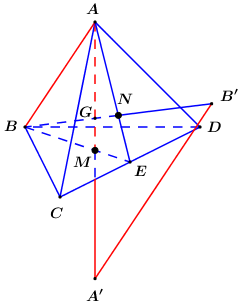
Bước 1: Tìm tỉ số đồng dạng của tứ diện \(A'B'C'D'\) đồng dạng với tứ diện \(ABCD\)
Dễ dàng nhận thấy tứ diện \(A'B'C'D'\) đồng dạng với tứ diện \(ABCD\) theo tỉ số \(k = \dfrac{{A'B'}}{{AB}}\).
Bước 2: Gọi \(M,\,\,N\) lần lượt là trong tâm tam giác \(BCD,\,\,ACD\), gọi \(G = AM \cap BN\). Tính \(\dfrac{{GA'}}{{GA}} = \dfrac{{A'B'}}{{AB}}\).
Gọi \(M,\,\,N\) lần lượt là trong tâm tam giác \(BCD,\,\,ACD\) ta có \(AM \bot \left( {BCD} \right),\,\,BN \bot \left( {ACD} \right)\). Gọi \(G = AM \cap BN\).
Ta có \(G\) là trọng tâm của tứ diện đều \(ABCD\) nên \(\dfrac{{AG}}{{AM}} = \dfrac{3}{4} \Rightarrow \dfrac{{AG}}{{AA'}} = \dfrac{3}{8} \Rightarrow \dfrac{{GA'}}{{GA}} = \dfrac{5}{3}\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{GA'}}{{GA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{5}{3} = k\).
Bước 3: Tính \(\dfrac{{{V_{A'B'C'D'}}}}{{{V_{ABCD}}}} = {k^3}\).
\( \Rightarrow \dfrac{{{V_{A'B'C'D'}}}}{{{V_{ABCD}}}} = {k^3} = \dfrac{{125}}{{27}}\).
Bước 4: Sử dụng công thức thể tích khối tứ diện đều cạnh \(a\) là \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
Mà \(ABCD\) là tứ diện đều cạnh \(1\) nên \({V_{ABCD}} = \dfrac{{\sqrt 2 }}{{12}}\).
Vậy \({V_{A'B'C'D'}} = \dfrac{{125}}{{37}}.\dfrac{{\sqrt 2 }}{{12}} = \dfrac{{125\sqrt 2 }}{{324}}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = 60^\circ .\) Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng \(60^\circ \)
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng AC và SB.
Tính thể tích khối chóp S.ABCD.
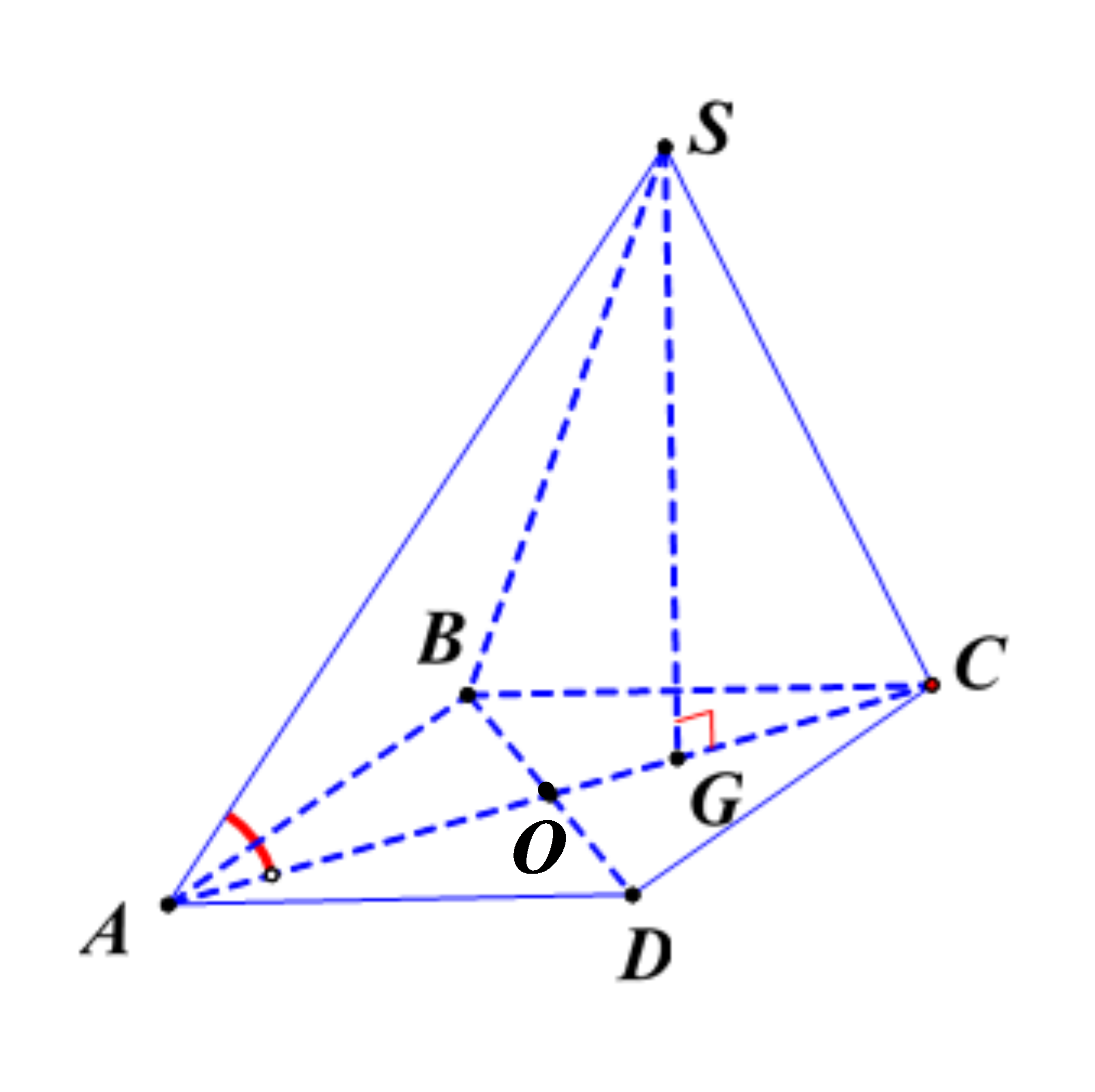
Bước 1: Tính AG.
Gọi O là giao điểm của AC và BD.
ABCD là hình thoi cạnh a nên BC=CD=a
\(\widehat {BAD} = \widehat {BCD} = {60^0}\)
=> Tam giác BCD là tam giác đều
=> \(CG = \dfrac{2}{3}.CO = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2}BC = \dfrac{{\sqrt 3 }}{3}a\)
=> \(AG = 2CG = \dfrac{{2\sqrt 3 }}{3}a\)
Bước 2: Xác định góc giữa SA và đáy trên hình.
Do SG vuông góc với (ABCD) nên góc giữa SA và đáy bằng góc giữa SA và hình chiếu của nó trên (ABCD) tức là góc giữa SA và GA.
=> \(\widehat {SAG} = {60^0}\)
Bước 3: Tính SG
Tam giác vuông SAG có \(\widehat {SAG} = {60^0}\) nên \(SG = AG\sqrt 3 = \dfrac{{2\sqrt 3 }}{3}a.\sqrt 3 = 2a\)
Bước 4: Tính thể tích S.ABCD.
Ta có \(AC = 3CG = 3.\dfrac{{\sqrt 3 }}{3}a = a\sqrt 3 \)
Diện tích hình thoi ABCD là: \(S = \dfrac{1}{2}.AC.BD = \dfrac{1}{2}.a\sqrt 3 .a = \dfrac{{{a^2}\sqrt 3 }}{2}\)
Thể tích S.ABCD: \(V = \dfrac{1}{3}SG.{S_{ABCD}} = \dfrac{1}{3}.2a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{3}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = 60^\circ .\) Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng \(60^\circ \)
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng AC và SB.
Tính khoảng cách giữa hai đường thẳng AC và SB.
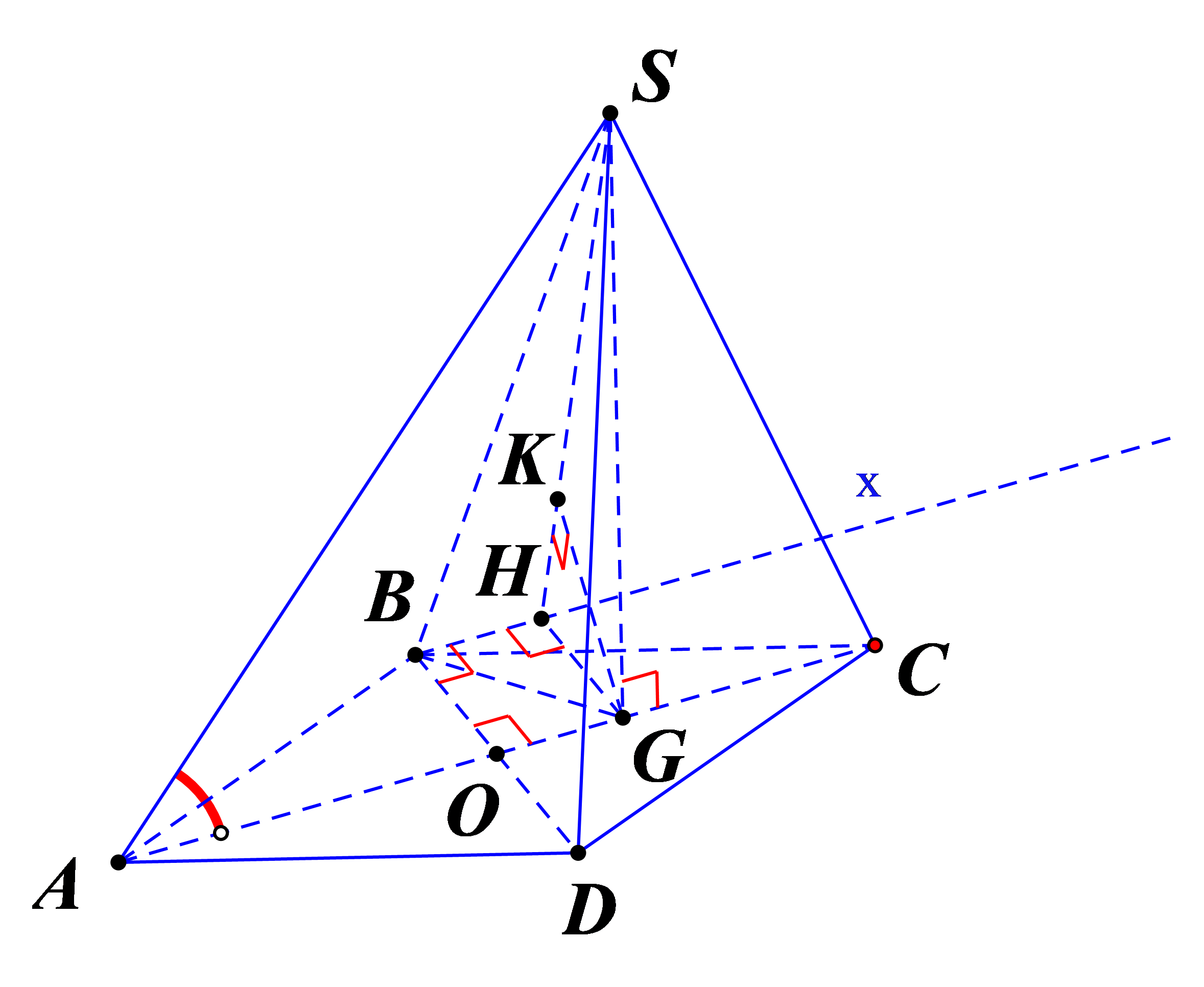
Kẻ Bx song song với AC.
Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}GH \bot BH\\BH \bot SG\end{array} \right\} \Rightarrow BH \bot \left( {SGH} \right)\\\left. \begin{array}{l} \Rightarrow BH \bot GK\\GK \bot SH\end{array} \right\} \Rightarrow GK \bot \left( {SHB} \right)\end{array}\)
Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)
Ta có BH//AC \( \Rightarrow AC//\left( {SHB} \right)\)
Mà \(SB \subset \left( {SHB} \right)\)
\( = > d\left( {SB,AC} \right)\)\( = d\left( {AC,\left( {SHB} \right)} \right)\)\( = d\left( {G,\left( {SHB} \right)} \right) = GK\)
Bước 3: Tính GK
Dễ thấy tứ giác OBHG là hình chữ nhật
=> \(HG = OB = \dfrac{a}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:
\(\dfrac{1}{{G{K^2}}} = \dfrac{1}{{S{G^2}}} + \dfrac{1}{{G{H^2}}}\)\( = \dfrac{1}{{4{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{17}}{{4{a^2}}}\)
\( \Rightarrow GK = \dfrac{{2\sqrt {17} a}}{{17}}\)
Vậy \(d\left( {SB,AC} \right) = \dfrac{{2a\sqrt {17} }}{{17}}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = 60^\circ .\) Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng \(60^\circ \)
Tính thể tích khối chóp $S.ABCD$.
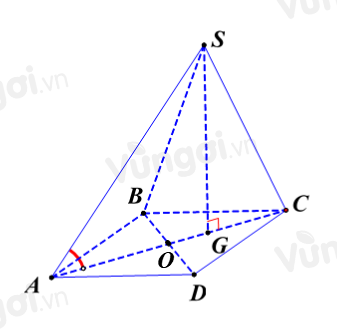
Bước 1: Tính AG.
Gọi O là giao điểm của AC và BD.
ABCD là hình thoi cạnh a nên BC=CD=a
\(\widehat {BAD} = \widehat {BCD} = {60^0}\)
=> Tam giác BCD là tam giác đều
=> \(CG = \dfrac{2}{3}.CO = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2}BC = \dfrac{{\sqrt 3 }}{3}a\)
=> \(AG = 2CG = \dfrac{{2\sqrt 3 }}{3}a\)
Bước 2: Xác định góc giữa SA và đáy trên hình.
Do SG vuông góc với (ABCD) nên góc giữa SA và đáy bằng góc giữa SA và hình chiếu của nó trên (ABCD) tức là góc giữa SA và GA.
=> \(\widehat {SAG} = {60^0}\)
Bước 3: Tính SG
Tam giác vuông SAG có \(\widehat {SAG} = {60^0}\) nên \(SG = AG\sqrt 3 = \dfrac{{2\sqrt 3 }}{3}a.\sqrt 3 = 2a\)
Bước 4: Tính thể tích S.ABCD.
Ta có \(AC = 3CG = 3.\dfrac{{\sqrt 3 }}{3}a = a\sqrt 3 \)
Diện tích hình thoi ABCD là: \(S = \dfrac{1}{2}.AC.BD = \dfrac{1}{2}.a\sqrt 3 .a = \dfrac{{{a^2}\sqrt 3 }}{2}\)
Thể tích S.ABCD: \(V = \dfrac{1}{3}SG.{S_{ABCD}} = \dfrac{1}{3}.2a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{3}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = 60^\circ .\) Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng \(60^\circ \)
Tính khoảng cách giữa hai đường thẳng AC và SB.
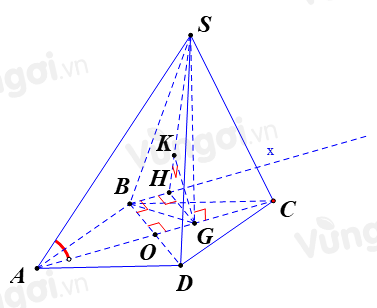
Kẻ Bx song song với AC.
Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}GH \bot BH\\BH \bot SG\end{array} \right\} \Rightarrow BH \bot \left( {SGH} \right)\\\left. \begin{array}{l} \Rightarrow BH \bot GK\\GK \bot SH\end{array} \right\} \Rightarrow GK \bot \left( {SHB} \right)\end{array}\)
Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)
Ta có BH//AC \( \Rightarrow AC//\left( {SHB} \right)\)
Mà \(SB \subset \left( {SHB} \right)\)
\( = > d\left( {SB,AC} \right)\)\( = d\left( {AC,\left( {SHB} \right)} \right)\)\( = d\left( {G,\left( {SHB} \right)} \right) = GK\)
Bước 3: Tính GK
Dễ thấy tứ giác OBHG là hình chữ nhật
=> \(HG = OB = \dfrac{a}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:
\(\dfrac{1}{{G{K^2}}} = \dfrac{1}{{S{G^2}}} + \dfrac{1}{{G{H^2}}}\)\( = \dfrac{1}{{4{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{17}}{{4{a^2}}}\)
\( \Rightarrow GK = \dfrac{{2\sqrt {17} a}}{{17}}\)
Vậy \(d\left( {SB,AC} \right) = \dfrac{{2a\sqrt {17} }}{{17}}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Lấy \(M,\,N\) lần lượt là trung điểm các cạnh \(SB,\,SD;\,K\) là giao điểm của mặt phẳng \(\left( {AMN} \right)\) và \(SC.\) Gọi \({V_1}\) là thể tích của khối chóp \(S.AMKN\), \({V_2}\) là thể tích của khối đa diện lồi \(AMKNBCD\). Tính \(\dfrac{{{V_1}}}{{{V_2}}}.\)
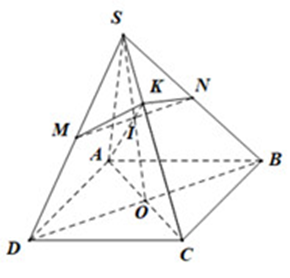
Gọi \(O\) là giao điểm của \(AC,BD\) . Gọi \(I\) là giao điểm của \(SO;MN\) . Ta có \(I\) là trung điểm \(SO\) và \(AI\) giao với \(SC\) tại \(K\).
Gọi \(H\) là trung điểm \(CK\) thì \(OH//AK\) (đường trung bình) suy ra \(K\) là trung điểm \(SH \Rightarrow \dfrac{{SK}}{{SC}} = \dfrac{1}{3}\)
Ta có: \(\dfrac{{{V_1}}}{{{V_1} + {V_2}}} = \dfrac{{{V_{S.AMKN}}}}{{{V_{S.ABCD}}}} = \dfrac{{2{V_{S.AMK}}}}{{2{V_{S.ACD}}}} = \dfrac{{SM}}{{SD}}.\dfrac{{SK}}{{SC}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6}\)
\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{5}\)
Đề thi THPT QG 2020 – mã đề 104
Cho hình chóp đều \(S.ABCD\) có tất cả các cạnh bằng \(a\) và \(O\) là tâm của đáy. Gọi \(M,N,P,Q\) lần lượt là các điểm đối xứng với \(O\) qua trọng tâm của các tam giác \(SAB,\,\,SBC,\,\,SCD,\,\,SDA\) và \(S'\) là điểm đối xứng với \(S\) qua \(O\). Thể tích khối chóp \(S'MNPQ\) bằng
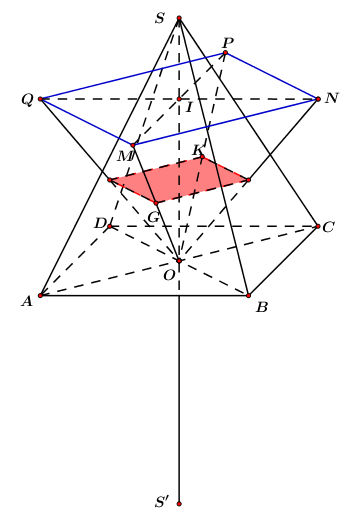
\(S.ABCD\) là hình chóp đều nên trọng tâm của các mặt bên tạo thành một hình vuông
=> MNPQ là hình vuông
Ta có : \(AC = a\sqrt 2 .\)
\( \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\)
Gọi \(G,\,\,K\) lần lượt là trọng tâm của \(\Delta SAB\) và \(\Delta SCD\).
\( \Rightarrow GK = \dfrac{2}{3}BC = \dfrac{2}{3}a = \dfrac{{2a}}{3}.\) (tính chất trọng tâm tam giác)
\( \Rightarrow MP = 2GK = \dfrac{4}{3}a\) (tính chất đường trung bình của tam giác)
Tương tự ta được: \(NQ = \dfrac{4}{3}a\).
\( \Rightarrow {S_{MNPQ}} = \dfrac{1}{2}MP.NQ = \dfrac{1}{2}.{\left( {\dfrac{4}{3}a} \right)^2} = \dfrac{8}{9}{a^2}\) .
Ta có: \(\left( {MNPQ} \right){\rm{//}}\left( {ABCD} \right)\)
\( \Rightarrow d\left( {M,\left( {ABCD} \right)} \right) = 2d\left( {G,\left( {ABCD} \right)} \right)\)\( = \dfrac{2}{3}SO = \dfrac{{a\sqrt 2 }}{3}\).
\( \Rightarrow d\left( {\left( {MNPQ} \right),\left( {ABCD} \right)} \right) = \dfrac{{a\sqrt 2 }}{3}\)
\( \Rightarrow d\left( {S',\left( {MNPQ} \right)} \right) = S'O + \dfrac{{a\sqrt 2 }}{3} = \dfrac{{5a\sqrt 2 }}{6}\)
\( \Rightarrow {V_{S'MNPQ}} = \dfrac{1}{3}.\dfrac{{5a\sqrt 2 }}{6}.\dfrac{{8{a^2}}}{9} = \dfrac{{20\sqrt 2 {a^3}}}{{81}}\).

