Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Lấy \(M,\,N\) lần lượt là trung điểm các cạnh \(SB,\,SD;\,K\) là giao điểm của mặt phẳng \(\left( {AMN} \right)\) và \(SC.\) Gọi \({V_1}\) là thể tích của khối chóp \(S.AMKN\), \({V_2}\) là thể tích của khối đa diện lồi \(AMKNBCD\). Tính \(\dfrac{{{V_1}}}{{{V_2}}}.\)
Trả lời bởi giáo viên
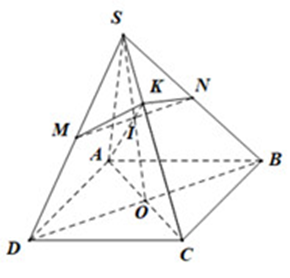
Gọi \(O\) là giao điểm của \(AC,BD\) . Gọi \(I\) là giao điểm của \(SO;MN\) . Ta có \(I\) là trung điểm \(SO\) và \(AI\) giao với \(SC\) tại \(K\).
Gọi \(H\) là trung điểm \(CK\) thì \(OH//AK\) (đường trung bình) suy ra \(K\) là trung điểm \(SH \Rightarrow \dfrac{{SK}}{{SC}} = \dfrac{1}{3}\)
Ta có: \(\dfrac{{{V_1}}}{{{V_1} + {V_2}}} = \dfrac{{{V_{S.AMKN}}}}{{{V_{S.ABCD}}}} = \dfrac{{2{V_{S.AMK}}}}{{2{V_{S.ACD}}}} = \dfrac{{SM}}{{SD}}.\dfrac{{SK}}{{SC}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6}\)
\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{5}\)
Hướng dẫn giải:
- Xác định điểm \(K\).
- Sử dụng tỉ số thể tích.

