Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = BC\sqrt 5 \), \(AC = 2BC\sqrt 2 \), hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(O\) của cạnh \(AC\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng 2. Mặt phẳng \(\left( {SBC} \right)\) hợp với mặt phẳng \(\left( {ABC} \right)\) một góc \(\alpha \) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt a }}{b}\), trong đó \(a,\,\,b \in {\mathbb{N}^*}\), \(a\) là số nguyên tố. Tổng \(a + b\) bằng:
Trả lời bởi giáo viên
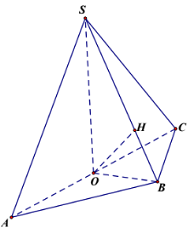
Gọi \(H\) là hình chiếu của \(O\) lên \(SB\).
Ta có: \(OB = \sqrt {\dfrac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC\), \(OC = \dfrac{1}{2}AC = BC\sqrt 2 \). Suy ra \(OB \bot BC\).
Dễ thấy \(\angle SBO = \alpha \) và \(OH = d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\).
Suy ra \(SO = \dfrac{{OH}}{{\cos \alpha }} = \dfrac{1}{{\cos \alpha }}\), \(OB = \dfrac{{OH}}{{\sin \alpha }} = \dfrac{1}{{\sin \alpha }}\).
\( \Rightarrow BC = OB = \dfrac{1}{{\sin \alpha }}\).
Thể tích khối chóp \(S.ABC\) là:
\(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}} = \dfrac{1}{3}SO.2{S_{OBC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{{\cos \alpha }}.{\left( {\dfrac{1}{{\sin \alpha }}} \right)^2} = \dfrac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}\end{array}\)
Áp dụng bất đẳng thức Cô-si ta có:
\(\begin{array}{l}1 = \dfrac{1}{2}{\sin ^2}\alpha + \dfrac{1}{2}{\sin ^2}\alpha + {\cos ^2}\alpha \ge 3.\sqrt[3]{{\dfrac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}\\ \Leftrightarrow \dfrac{1}{{27}} \ge \dfrac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \dfrac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \dfrac{{3\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABC}} \ge \dfrac{{\sqrt 3 }}{2}\end{array}\)
Vậy \(\min {V_{S.ABC}} = \dfrac{{\sqrt 3 }}{2}\). Dấu “=” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = \dfrac{1}{2}{\sin ^2}\alpha = \dfrac{1}{3} \Leftrightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{3}\).
\( \Rightarrow a = 3,\,\,b = 2\).
Vậy \(a + b = 3 + 2 = 5\).

