Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = 60^\circ .\) Hình chiếu vuông góc của S lên mặt phẳng đáy là trọng tâm G của tam giác BCD, góc giữa SA và đáy bằng \(60^\circ \)
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng AC và SB.
Tính khoảng cách giữa hai đường thẳng AC và SB.
Trả lời bởi giáo viên
Đáp án đúng: a
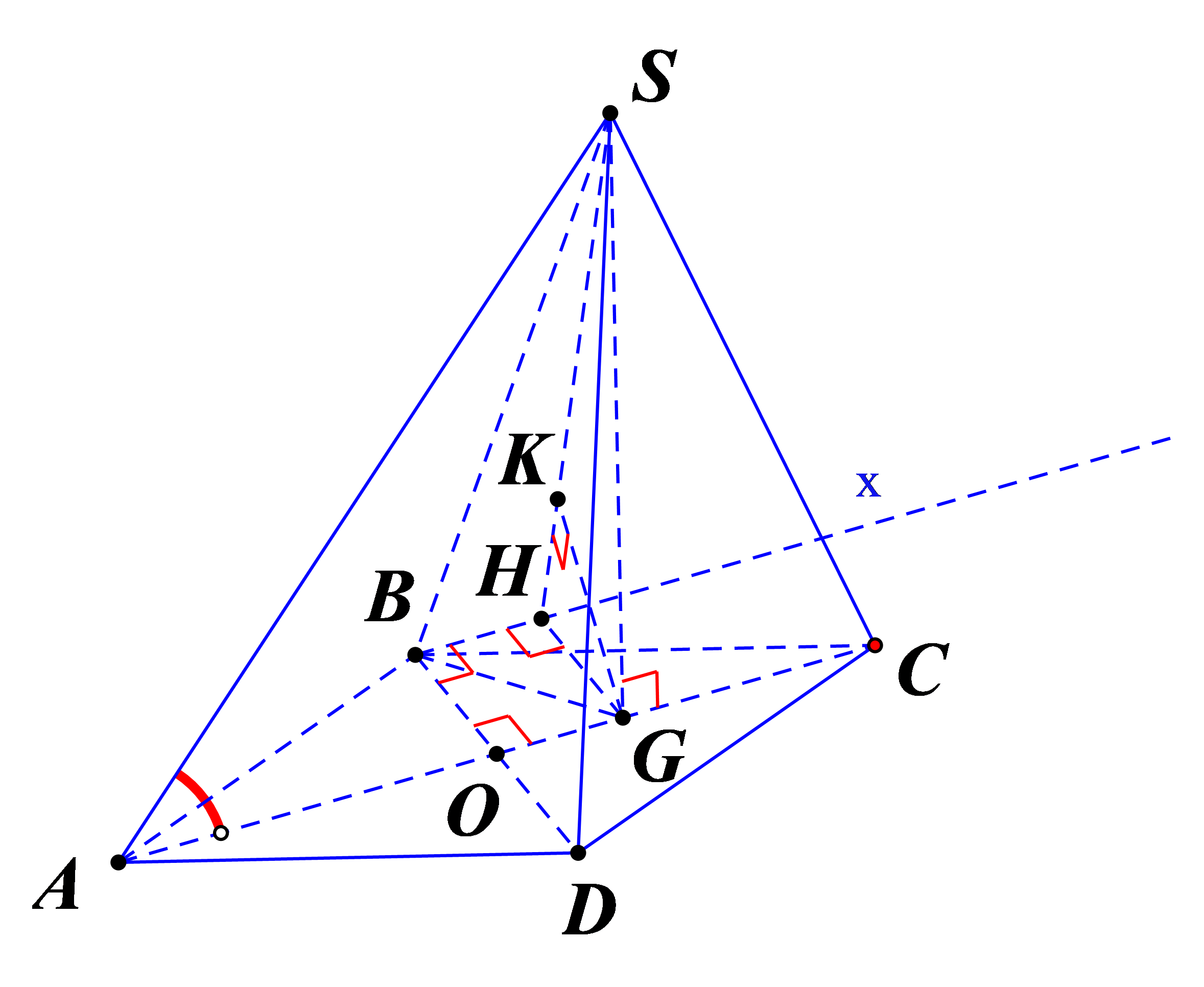
Kẻ Bx song song với AC.
Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}GH \bot BH\\BH \bot SG\end{array} \right\} \Rightarrow BH \bot \left( {SGH} \right)\\\left. \begin{array}{l} \Rightarrow BH \bot GK\\GK \bot SH\end{array} \right\} \Rightarrow GK \bot \left( {SHB} \right)\end{array}\)
Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)
Ta có BH//AC \( \Rightarrow AC//\left( {SHB} \right)\)
Mà \(SB \subset \left( {SHB} \right)\)
\( = > d\left( {SB,AC} \right)\)\( = d\left( {AC,\left( {SHB} \right)} \right)\)\( = d\left( {G,\left( {SHB} \right)} \right) = GK\)
Bước 3: Tính GK
Dễ thấy tứ giác OBHG là hình chữ nhật
=> \(HG = OB = \dfrac{a}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:
\(\dfrac{1}{{G{K^2}}} = \dfrac{1}{{S{G^2}}} + \dfrac{1}{{G{H^2}}}\)\( = \dfrac{1}{{4{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{17}}{{4{a^2}}}\)
\( \Rightarrow GK = \dfrac{{2\sqrt {17} a}}{{17}}\)
Vậy \(d\left( {SB,AC} \right) = \dfrac{{2a\sqrt {17} }}{{17}}\)
Hướng dẫn giải:
Kẻ Bx song song với AC. Kẻ GH vuông góc với Bx, GK vuông góc với SH
Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)
Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)
Bước 3: Tính GK
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
