Câu hỏi:
2 năm trước
Cho hình tứ diện đều \(ABCD\) có độ dài các cạnh bằng \(1\). Gọi \(A',\,\,B',\,\,C',\,\,D'\) lần lượt là điểm đối xứng của \(A,\,\,B,\,\,C,\,\,D\) qua các mặt phẳng \(\left( {BCD} \right),\,\,\left( {ACD} \right),\,\,\left( {ABD} \right),\,\,\left( {ABC} \right)\). Tính thể tích của khối tứ diện \(A'B'C'D'\).
Trả lời bởi giáo viên
Đáp án đúng: a
Bước 1: Tìm tỉ số đồng dạng của tứ diện \(A'B'C'D'\) đồng dạng với tứ diện \(ABCD\)
Dễ dàng nhận thấy tứ diện \(A'B'C'D'\) đồng dạng với tứ diện \(ABCD\) theo tỉ số \(k = \dfrac{{A'B'}}{{AB}}\).
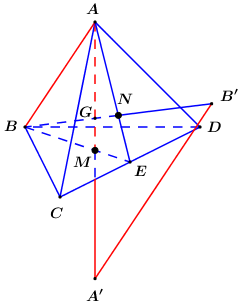
Bước 2: Gọi \(M,\,\,N\) lần lượt là trong tâm tam giác \(BCD,\,\,ACD\), gọi \(G = AM \cap BN\). Tính \(\dfrac{{GA'}}{{GA}} = \dfrac{{A'B'}}{{AB}}\).
Gọi \(M,\,\,N\) lần lượt là trong tâm tam giác \(BCD,\,\,ACD\) ta có \(AM \bot \left( {BCD} \right),\,\,BN \bot \left( {ACD} \right)\). Gọi \(G = AM \cap BN\).
Ta có \(G\) là trọng tâm của tứ diện đều \(ABCD\) nên \(\dfrac{{AG}}{{AM}} = \dfrac{3}{4} \Rightarrow \dfrac{{AG}}{{AA'}} = \dfrac{3}{8} \Rightarrow \dfrac{{GA'}}{{GA}} = \dfrac{5}{3}\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{GA'}}{{GA}} = \dfrac{{A'B'}}{{AB}} = \dfrac{5}{3} = k\).
Bước 3: Tính \(\dfrac{{{V_{A'B'C'D'}}}}{{{V_{ABCD}}}} = {k^3}\).
\( \Rightarrow \dfrac{{{V_{A'B'C'D'}}}}{{{V_{ABCD}}}} = {k^3} = \dfrac{{125}}{{27}}\).
Bước 4: Sử dụng công thức thể tích khối tứ diện đều cạnh \(a\) là \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
Mà \(ABCD\) là tứ diện đều cạnh \(1\) nên \({V_{ABCD}} = \dfrac{{\sqrt 2 }}{{12}}\).
Vậy \({V_{A'B'C'D'}} = \dfrac{{125}}{{37}}.\dfrac{{\sqrt 2 }}{{12}} = \dfrac{{125\sqrt 2 }}{{324}}\).
Hướng dẫn giải:
Bước 1: Tìm tỉ số đồng dạng của tứ diện \(A'B'C'D'\) đồng dạng với tứ diện \(ABCD\)
Bước 2: Gọi \(M,\,\,N\) lần lượt là trong tâm tam giác \(BCD,\,\,ACD\), gọi \(G = AM \cap BN\). Tính \(\dfrac{{GA'}}{{GA}} = \dfrac{{A'B'}}{{AB}}\).
Bước 3: Tính \(\dfrac{{{V_{A'B'C'D'}}}}{{{V_{ABCD}}}} = {k^3}\).
Bước 4: Sử dụng công thức tính nhanh: Thể tích khối tứ diện đều cạnh \(a\) là \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
