Phương trình mũ và một số phương pháp giải

Đặt $\left| {x - 1} \right| = a$ khi đó phương trình trở thành ${2^{a + 1}} + {2^a} + m = 0$ (1)

Để phương trình đã cho có nghiệm duy nhất thì pt (1) bắt buộc phải có nghiệm duy nhất $a=0$ ( vì nếu $a>0$ thì sẽ tồn tại 2 giá trị của $x$)

Nên ${2^1} + {2^0} + m = 0$. Suy ra $m =  - 3$

Điều kiện : $x \ne 0$

Với $x < 0$  ta có $\left\{ \begin{array}{l}x + \dfrac{1}{{4x}} < 0\\\dfrac{x}{4} + \dfrac{1}{x} < 0\end{array} \right.$ $\Rightarrow \left\{ \begin{array}{l}{2^{x + \frac{1}{{4x}}}} < 1\\{2^{\frac{x}{4} + \frac{1}{x}}} < 1\end{array} \right.$ $\Rightarrow {2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} < 2$

⇒ Phương trình không có nghiệm $x < 0$

Với $x > 0$, áp dụng bất đẳng thức Côsi cho hai số dương ta được.

$\left\{ \begin{array}{l}x + \dfrac{1}{{4x}} \ge 2\sqrt {x.\dfrac{1}{{4x}}}  = 1\\\dfrac{x}{4} + \dfrac{1}{x} \ge 2\sqrt {\dfrac{x}{4}.\dfrac{1}{x}}  = 1\end{array} \right.$ $\Rightarrow \left\{ \begin{array}{l}{2^{x + \frac{1}{{4x}}}} \ge 2\\{2^{\frac{x}{4} + \frac{1}{x}}} \ge 2\end{array} \right.$ $\Rightarrow {2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} \ge 4$

Dấu “=” xảy ra khi và chỉ khi $\left\{ \begin{array}{l}x = \dfrac{1}{{4x}}\\\dfrac{x}{4} = \dfrac{1}{x}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} 4{x^2} = 1\\ {x^2} = 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x^2} = \frac{1}{4}\\ {x^2} = 4 \end{array} \right.$(không xảy ra)

Vậy ${2^{x + \frac{1}{{4x}}}} + {2^{\frac{x}{4} + \frac{1}{x}}} > 4$ nên phương trình vô nghiệm

$\begin{array}{l}x\left( {{2^{x - 1}} + 4} \right) = {2^{x + 1}} + {x^2} \Leftrightarrow x{.2^{x - 1}} - {4.2^{x - 1}} + 4x - {x^2} = 0 \Leftrightarrow \left( {x - 4} \right)\left( {{2^{x - 1}} - x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 4\\{2^{x - 1}} - x = 0\,\left( * \right)\end{array} \right.\end{array}$

Xét hàm số $f\left( x \right) = {2^{x - 1}} - x$ trên $\mathbb{R}$ . Ta có

$f'\left( x \right) = {2^{x - 1}}\ln 2 - 1 = 0 \Leftrightarrow x = {x_0} = 1 + {\log _2}\left( {\dfrac{1}{{\ln 2}}} \right)$

$f'\left( x \right) < 0 \Leftrightarrow x < {x_0};f'\left( x \right) > 0 \Leftrightarrow x > {x_0}$

nên phương trình $f(x) = 0$ có tối đa 1 nghiệm trong các khoảng $\left( {-\infty ;{x_0}} \right)$  và $\left( {{x_0}; + \infty } \right)$

Mà $f\left( 1 \right) = f\left( 2 \right) = 0$  nên phương trình (*) có 2 nghiệm $x = 1$ và $x = 2$

Tổng các nghiệm của phương trình đã cho là $7$.

Ta có: $1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x$

$\Leftrightarrow \left[ {\left( {{x^2} - {m^2}x - 1} \right) + \left( {{x^2} - mx - 1} \right)} \right]{.2^{ - \left( {{x^2} - mx - 1} \right)}} = \left( {{x^2} - mx - 1} \right){.2^{\left( {{x^2} - {m^2}x - 1} \right) - \left( {{x^2} - mx - 1} \right)}} + {x^2} - {m^2}x - 1$

Đặt $\left\{ \begin{array}{l}u = {x^2} - {m^2}x - 1\\v = {x^2} - mx - 1\end{array} \right.$. Phương trình trở thành: $\left( {u + v} \right){.2^{ - v}} = v{.2^{u - v}} + u \Leftrightarrow u\left( {{2^{ - v}} - 1} \right) = v{2^{ - v}}\left( {{2^u} - 1} \right)$ (*)

+) Dễ dàng kiểm tra $u = 0$ hoặc $v = 0$ là nghiệm của (*)

+) Với $u,v \ne 0$, $\left( * \right) \Leftrightarrow \dfrac{{{2^{ - v}} - 1}}{{v{2^{ - v}}}} = \dfrac{{{2^u} - 1}}{u}$

$\Leftrightarrow \dfrac{{{2^u} - 1}}{u} = \dfrac{{1 - {2^v}}}{v}$

$\Leftrightarrow \dfrac{{{2^u} - 1}}{u} + \dfrac{{{2^v} - 1}}{v} = 0$

Xét hàm $f\left( t \right) = \frac{{{2^t} - 1}}{t}$ trên $\mathbb{R}\backslash \left\{ 0 \right\}$ ta thấy:

+) Với $t > 0$ thì $\left\{ \begin{array}{l}{2^t} - 1 > 0\\t > 0\end{array} \right.$ $\Rightarrow \frac{{{2^t} - 1}}{t} > 0$ $\Rightarrow f\left( t \right) > 0$.

+) Với $t < 0$ thì $\left\{ \begin{array}{l}{2^t} - 1 < 0\\t < 0\end{array} \right. \Rightarrow \frac{{{2^t} - 1}}{t} > 0$ $\Rightarrow f\left( t \right) > 0$.

Do đó $f\left( t \right) > 0$ với mọi $t \ne 0$.

$\Rightarrow f\left( u \right) > 0,f\left( v \right) > 0,\forall u,v \ne 0$

$\Rightarrow f\left( u \right) + f\left( v \right) > 0,\forall u,v \ne 0$

$\Rightarrow \frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} > 0,\forall u,v \ne 0$

Do đó phương trình $\frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} = 0$ vô nghiệm.

Vậy $\left[ \begin{array}{l}u = 0\\v = 0\end{array} \right.$

$\Leftrightarrow$$\left[ \begin{array}{l}{x^2} - {m^2}x - 1 = 0\,\,\,(1)\\{x^2} - mx - 1 = 0\,\,\,\,(2)\end{array} \right.$

Hai phương trình trên luôn có hai nghiệm phân biệt, tổng hai nghiệm ở mỗi phương trình là:

${S_1} = {m^2},\,{S_2} = m \Rightarrow S = {m^2} + m \ge  - \dfrac{1}{4}$.

Vậy tổng các nghiệm của phương trình đã cho nhỏ nhất là $- \dfrac{1}{4}$ khi $m =  - \dfrac{1}{2}$.

Đặt $\left\{ \begin{array}{l}a = {5^x}\\b = {5^{2y}}\\c = {5^{3z}}\end{array} \right.$, với $x,\,\,y,\,\,z \ge 0$ thì $a,\,\,b,\,\,c \ge 1$.

Theo bài ra ta có $a + b + c = 2020$ $\Rightarrow 1 \le a,b,c \le 2018$.

Ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\left( {a - 1} \right)\left( {b - 1} \right)\left( {c - 1} \right) \ge 0\\ \Leftrightarrow \left( {ab - a - b + 1} \right)\left( {c - 1} \right) \ge 0\\ \Leftrightarrow abc + \left( {a + b + c} \right) - \left( {ab + bc + ca} \right) - 1 \ge 0\,\,\,\,\left( 1 \right)\\\,\,\,\,\,\,\left( {a - 2018} \right)\left( {b - 2018} \right)\left( {c - 2018} \right) \le 0\\ \Leftrightarrow \left( {ab - 2018\left( {a + b} \right) + {{2018}^2}} \right)\left( {c - 2018} \right) \le 0\\ \Leftrightarrow abc + {2018^2}\left( {a + b + c} \right) - 2018\left( {ab + bc + ca} \right) - {2018^3} \le 0\,\,\,\left( 2 \right)\end{array}$

Lấy (1) nhân với 2018 rồi trừ đi (2) ta được:

$\begin{array}{l}\,\,\,\,\,2017abc + \left( {2018 - {{2018}^2}} \right)\left( {a + b + c} \right) - 2018 + {2018^3} \ge 0\\ \Leftrightarrow 2017abc + 2018\left( {1 - 2018} \right)\left( {a + b + c} \right) + {2018^3} - 2018 \ge 0\\ \Leftrightarrow 2017abc - 2017.2018.\left( {a + b + c} \right) + {2018^3} - 2018 \ge 0\\ \Leftrightarrow {2017.5^x}{.5^{2y}}{.5^{3z}} - 2017.2018.2020 + {2018^3} - 2018 \ge 0\\ \Leftrightarrow {2017.5^x}{.5^{2y}}{.5^{3z}} + 2018\left( {{{2018}^2} - 2017.2020 - 1} \right) \ge 0\\ \Leftrightarrow {2017.5^x}{.5^{2y}}{.5^{3z}} - 2017.2018 \ge 0\\ \Leftrightarrow {5^x}{.5^{2y}}{.5^{3z}} - 2018 \ge 0\\ \Leftrightarrow {5^x}{.5^{2y}}{.5^{3z}} \ge 2018\\ \Leftrightarrow {5^{x + 2y + 3z}} \ge 2018\\ \Leftrightarrow x + 2y + 3z \ge {\log _5}2018\\ \Leftrightarrow \dfrac{{x + 2y + 3z}}{6} \ge \dfrac{1}{6}{\log _5}2018\\ \Leftrightarrow \dfrac{x}{6} + \dfrac{y}{3} + \dfrac{z}{2} \ge \dfrac{1}{6}{\log _5}2018\end{array}$  

Vậy giá trị nhỏ nhất của biểu tức $T = \dfrac{x}{6} + \dfrac{y}{3} + \dfrac{z}{2}$ là $\dfrac{1}{6}{\log _5}2018$.

* pt $\Leftrightarrow 27{\,^{3{x^2} + xy - 9x}} = xy + 1$.

$\Rightarrow xy + 1 > 0 \Leftrightarrow y >  - \dfrac{1}{x}$, khi $x \in \left( {\dfrac{1}{3};3} \right)$ $\Rightarrow y >  - 3$ thì mới tồn tại $x \in \left( {\dfrac{1}{3};3} \right)$.

$\Rightarrow$ Ta chặn được $y >  - 3$  =>$y \ge  - 2$.

* $pt \Leftrightarrow {27^{3{x^2} + xy - 9x}} - xy - 1 = 0$.

Đặt $f\left( x \right) = g\left( y \right) = {27^{3{x^2} + xy - 9x}} - xy - 1$ ta có $\left\{ \begin{array}{l}f\left( {\dfrac{1}{3}} \right) = {3^{y - 8}} - \dfrac{y}{3} - 1\\f\left( 3 \right) = {27^{3y}} - 3y - 1\end{array} \right.$.

Nhận thấy ngay $f\left( 3 \right) \ge 0\,\,\forall y \in \mathbb{Z}$, chỉ bằng 0 tại $y = 0$.

+ Xét $y = 0 \Rightarrow$ thay vào phương trình ban đầu $\Rightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.$, loại vì không có nghiệm thuộc $\left( {\dfrac{1}{3};3} \right)$.

+ Xét $y \ne 0 \Rightarrow f\left( 3 \right) > 0\,\,\forall x \in {\mathbb{Z}^*}$.

1) Ta Table khảo sát $f\left( {\dfrac{1}{3}} \right)$ với $\left\{ \begin{array}{l}Start:\,\,y =  - 2\\End:\,\,y = 17\\Step:\,\,\, = 1\end{array} \right.$

$\Rightarrow f\left( {\dfrac{1}{3}} \right) < 0\,\,\forall y \in \left\{ { - 2; - 1;1;2;...;9} \right\}$.

$\Rightarrow f\left( {\dfrac{1}{3}} \right).f\left( 3 \right) < 0\,\,\forall y \in \left\{ { - 2; - 1;1;2;...;9} \right\}$

$\Rightarrow$ Có 11 giá trị của $y$ để tồn tại nghiệm $x \in \left( {\dfrac{1}{3};3} \right)$.

2) Từ bảng Table ta nhận thấy khi $y \ge 10$ thì $f\left( {\dfrac{1}{3}} \right) > 0$ và đồng biến.

Ta đi chứng minh khi $y \ge 10$ thì phương trình vô nghiệm.

$g'\left( y \right) = x\left( {{{27}^{3{x^2} + x\left( {y - 9} \right)}}.\ln 27 - 1} \right) > 0\,\,\left\{ \begin{array}{l}\forall y \ge 10\\x \in \left( {\dfrac{1}{3};3} \right)\end{array} \right.$

$\Rightarrow g\left( y \right) \ge g\left( {10} \right) = {27^{3{x^2} + x}} - 10x - 1 = h\left( x \right)$.

Ta có $h'\left( x \right) = {27^{3{x^2} + x}}\left( {6x + 1} \right)\ln 27 - 10 > 0\,\,\forall x \in \left( {\dfrac{1}{3};3} \right)$.

$\Rightarrow h\left( x \right) > h\left( {\dfrac{1}{3}} \right) = \dfrac{{14}}{3} > 0$.

$\Rightarrow$ Phương trình vô nghiệm với $x \in \left( {\dfrac{1}{3};3} \right)$.

Vậy đáp số có 11 giá trị nguyên của $y$.

Bước 1: Sử dụng hàm đặc trưng, tìm biểu diễn ${x^3}$ theo $y$.

Ta có ${2^{{x^3} - y + 1}} = \dfrac{{2x + y}}{{2{x^3} + 4x + 4}}$

$\begin{array}{l} \Leftrightarrow {2^{{x^3} + 2x + 2 - 2x - y - 1}} = \dfrac{{2x + y}}{{2{x^3} + 4x + 4}}\\ \Leftrightarrow \dfrac{{{2^{{x^3} + 2x + 2}}}}{{{2^{2x + y}}.2}} = \dfrac{{2x + y}}{{2\left( {{x^3} + 2x + 2} \right)}}\\ \Leftrightarrow {2^{{x^3} + 2x + 2}}\left( {{x^3} + 2x + 2} \right) = {2^{2x + y}}.\left( {2x + y} \right)\,\,\,\left( * \right)\end{array}$

Xét $f\left( t \right) = {2^t}.t,\,\,t > 0$ ta có $f'\left( t \right) = {2^t} + t{.2^t}.\ln 2 > 0;\,\,\forall t > 0$. Do đó hàm số $f\left( t \right)$ đồng biến trên $\left( {0; + \infty } \right)$.

Do đó $\left( * \right) \Leftrightarrow {x^3} + 2x + 2 = 2x + y \Rightarrow {x^3} = y - 2$

Bước 2: Thế vào biểu thức $P$, sử dụng BĐT Cô-si tìm GTNN của biểu thức $P$.

Khi đó $P = \dfrac{7}{y} + \dfrac{{{x^3}}}{7} = \dfrac{7}{y} + \dfrac{{y - 2}}{7} = \dfrac{7}{y} + \dfrac{y}{7} - \dfrac{2}{7} \ge 2\sqrt {\dfrac{7}{y}.\dfrac{y}{7}}  - \dfrac{2}{7} = \dfrac{{12}}{7}$.

Dấu “=” xảy ra $\Leftrightarrow \dfrac{7}{y} = \dfrac{y}{7} \Leftrightarrow y = 7\,\,\left( {do\,\,y > 0} \right)$.

${P_{\min }} = \dfrac{{12}}{7} \Leftrightarrow x = \sqrt[3]{5},\,\,y = 7$.

Vậy $a=12,b=7=>a-b=5$

${25^{x + 1}} - {5^{x + 2}} - 4m = 0$$\Leftrightarrow {\left( {{5^{x + 1}}} \right)^2} - {5.5^{x + 1}} - 4m = 0 \Leftrightarrow 4m = {\left( {{5^{x + 1}}} \right)^2} - {5.5^{x + 1}}$

Đặt $t = {5^{x + 1}} \Rightarrow 0 < t < 25$

Phương trình trên trở thành $4m = {t^2} - 5t \Leftrightarrow m = \dfrac{{{t^2}}}{4} - \dfrac{5}{4}t = f\left( t \right)$(1)

Bảng biến thiên của hàm số y=f(t) trên (0;25)

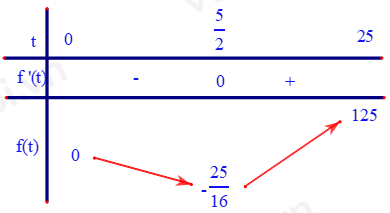
Phương trình (1) có nghiệm trên (0;25) khi và chỉ khi $\dfrac{{ - 25}}{{16}} \le m < 125 \Leftrightarrow  - 1 \le m \le 124$

Tổng các giá trị của m là:

-1+0+1+2+…+124=7749

Ta có ${4^{{a^2} + b}} \le {3^{b - a}} + 65 \Leftrightarrow {4^{{a^2} + b}} - {3^{b - a}} - 65 \le 0$

$\Leftrightarrow {4^{{a^2}}} - \dfrac{{{3^{b - a}}}}{{{4^b}}} - \dfrac{{65}}{{{4^b}}} \le 0$$\Leftrightarrow  - {\left( {\dfrac{3}{4}} \right)^b} \cdot \dfrac{1}{{{3^a}}} - 65 \cdot {\left( {\dfrac{1}{4}} \right)^b} + {4^{{a^2}}} \le 0$

Xét hàm số $f\left( b \right) =  - {\left( {\dfrac{3}{4}} \right)^b} \cdot \dfrac{1}{{{3^a}}} - 65 \cdot {\left( {\dfrac{1}{4}} \right)^b} + {4^{{a^2}}},$$b \in \left( { - 12;12} \right)$

$\Rightarrow {f^\prime }\left( b \right) =  - \ln \left( {\dfrac{3}{4}} \right) \cdot {\left( {\dfrac{3}{4}} \right)^b} \cdot \dfrac{1}{{{3^a}}}$$- 65\ln \left( {\dfrac{1}{4}} \right) \cdot {\left( {\dfrac{1}{4}} \right)^b} > 0$.

=> $f (b)$ đồng biến.

Để $f\left( b \right) \le 0$ có ít nhất 4 nghiệm nguyên thì $f\left( { - 8} \right) \le 0 \Leftrightarrow {4^{{a^2} - 8}} \le {3^{ - a - 8}} + 65$ $\Rightarrow {4^{{a^2} - 8}} \le 65 \Rightarrow {a^2} - 8 \le {\log _4}65$.

Do $a \in \mathbb{Z} \Rightarrow a \in  - 3; - 2; \ldots 3$. Có 7 giá trị nguyên của $a$.