Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
\(\begin{array}{l}{4.9^x} - {13.6^x} + {9.4^x} = 0 \Leftrightarrow 4 - 13.{\left( {\dfrac{2}{3}} \right)^x} + 9.{\left( {\dfrac{2}{3}} \right)^{2x}} = 0 \Leftrightarrow \left[ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^x} = 1\\{\left( {\dfrac{2}{3}} \right)^x} = \dfrac{4}{9}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right. \Rightarrow T = 0 + 2 = 2\end{array}\)
Tìm tập nghiệm S của phương trình: ${4^{x + 1}} + {4^{x - 1}} = 272$
Thử lần lượt từng đáp án ta thấy $x = 3$ là nghiệm của phương trình
Giải phương trình \(\sqrt {{3^x} + 6} = {3^x}\) có tập nghiệm bằng:
Đặt
\(\begin{array}{l}t = {3^x},t > 0 \Rightarrow \sqrt {t + 6} = t \to t + 6 = {t^2} \Rightarrow \left[ \begin{array}{l}t = - 2(l)\\t = 3\end{array} \right.\\t = 3 \Rightarrow {3^x} = 3 \Rightarrow x = 1\end{array}\)
Tìm tích các nghiệm của phương trình \({(\sqrt 2 - 1)^x} + {(\sqrt 2 + 1)^x} - 2\sqrt 2 = 0\)
Đặt $t = {\left( {\sqrt 2 - 1} \right)^x}\left( {t > 0} \right)$ phương trình có dạng $t + \dfrac{1}{t} = 2\sqrt 2 \Leftrightarrow {t^2} - 2\sqrt 2 t + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \sqrt 2 + 1} (tm)\\{t = \sqrt 2 - 1} (tm) \end{array}} \right.$
Khi đó
$\begin{array}{l}t = \sqrt 2 + 1 \Rightarrow x = - 1\\t = \sqrt 2 - 1 \Rightarrow x = 1\end{array}$
Suy ra tích các nghiệm bằng $-1$.
Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .
Đặt $t = {2^x};x \in \left( {1;3} \right) \Rightarrow t = {2^x} \in \left( {2;8} \right)$
Xét hàm số \(y = {t^2} - 8t + 3\) trên \((2;8)\) có:
$y' = 2t - 8;$ $y' = 0 \Leftrightarrow 2t - 8 = 0 \Leftrightarrow t = 4\in (2;8)$
Bảng biến thiên:
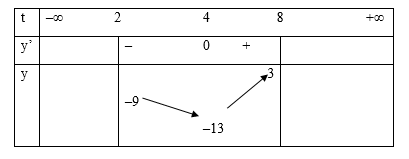
Căn cứ bảng biến thiên:
Phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm \(x \in \left( {1;3} \right) \Leftrightarrow - 13 < m < - 9\)
Tìm tập hợp tất cả các tham số $m$ sao cho phương trình ${4^{{x^2} - 2x + 1}} - m{.2^{{x^2} - 2x + 2}} + 3m - 2 = 0$ có 4 nghiệm phân biệt.
Đặt $t = {2^{{x^2} - 2x + 1}} \ge 1$, phương trình đã cho trở thành ${t^2} - 2mt + 3m - 2 = 0{\rm{ }}\left( * \right)$
Với $t = 1$ ta tìm được 1 giá trị của $x$
Với $t > 1$ ta tìm được 2 giá trị của $x$
Do đó, phương trình đã cho có 4 nghiệm phân biệt
⇔ Phương trình (*) có 2 nghiệm phân biệt lớn hơn $1$
$\left\{ \begin{array}{l}\Delta ' = {m^2} - \left( {3m - 2} \right) > 0\\\left( {{t_1} - 1} \right) + \left( {{t_2} - 1} \right) > 0\\\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 2 > 0\\{t_1} + {t_2} > 2\\{t_1}{t_2} - \left( {{t_1} + {t_2}} \right) + 1 > 0\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 2 > 0\\2m > 2\\3m - 2 - 2m + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\\m > 1\end{array} \right.$
⇔ $m > 2$
Các giá trị thực của tham số $m$ để phương trình : ${12^x} + \left( {4 - m} \right){.3^x} - m = 0$ có nghiệm thuộc khoảng $\left( { - 1;0} \right)$ là:
- Từ các đáp án đã cho, ta thấy giá trị $m=2$ không thuộc đáp án C nên ta thử $m=2$ có thỏa mãn bài toán hay không sẽ loại được đáp án.
Thử với $m=2$ ta được phương trình : \({12^x} + {2.3^x} - 2 = 0;\) \( f( - 1) = \dfrac{{ - 5}}{4};\) \(f(0) = 1\) \( \Rightarrow f(0).f( - 1) < 0\)
Do đó, phương trình có nghiệm trong khoảng $(-1;0)$, mà đáp án C không chứa $m=2$ nên loại C.
- Lại có giá trị $m=3$ thuộc đáp án C nhưng không thuộc hai đáp án A và D nên nếu kiểm tra $m=3$ ta có thể loại tiếp được đáp án.
Thử với $m=3$ ta được phương trình : \({12^x} + {3^x} - 3 = 0;\) \(f( - 1) = \dfrac{{ - 31}}{{12}};\) \(f(0) = - 1\) \( \Rightarrow f(0).f( - 1) > 0\)
Mà hàm số này đồng biến khi $m=3$ nên $f(x)<0,\forall x\in (-1;0)$, suy ra phương trình $f(x)=0$ sẽ không có nghiệm trong $(-1;0)$, loại B.
- Cuối cùng, ta thấy giá trị $m=1$ thuộc đáp án A và không thuộc đáp án D nên ta sẽ thử $m=1$ để loại đáp án.
Thử với $m=1$ ta được phương trình : \({12^x} + {3.3^x} - 1 = 0;\) \(f( - 1) = \dfrac{{ - 11}}{{12}};\,f(0) = 3\) \( \Rightarrow f(0).f( - 1) < 0\)
Do đó phương trình $f(x)=0$ sẽ có nghiệm trong $(-1;0)$ nên loại D và chọn A.
Tìm giá trị của tham số $m$ để phương trình ${9^x} - m{.3^{x + 2}} + 9m = 0$ có hai nghiệm phân biệt ${x_1};{x_2}$ thỏa mãn ${x_1} + {x_2} = 3$
Phương trình tương đương với: \({3^{2x}} - 9m{.3^x} + 9m = 0\) (*)
Đặt ${3^x} = a$ với $a > 0$ phương trình thành: ${a^2} - 9m.a + 9m = 0$
Giả sử phương trình có 2 nghiệm ${x_1}$ và ${x_2}$ thì \({3^{{x_1}}};{3^{{x_2}}}\) lần lượt là nghiệm của (*)
Suy ra: \({3^{{x_1}}}{.3^{{x_2}}} = 9m \Leftrightarrow {3^{{x_1} + {x_2}}} = 9m \Leftrightarrow {x_1} + {x_2} = {\log _3}9m = 3 \Rightarrow 9m = 27 \Leftrightarrow m = 3\)
Tìm tập hợp tất cả các giá trị của tham số thực $m$ để phương trình sau có 2 nghiệm phân biệt: \({9^{1 - x}} + 2(m - 1){3^{1 - x}} + 1 = 0\)
Thử với $m = -1$ ta được phương trình:
${\left( {{3^{1 - x}}} \right)^2} - {4.3^{1 - x}} + 1 = 0$ phải có 2 nghiệm $3^{1-x}$ đều dương và 2 nghiệm đó là \(2 - \sqrt 3 \) và $2 + \sqrt 3 $.
Vậy $m = - 1$ thỏa mãn nên ta loại được A; B; D
Cho số thực $x$ thỏa mãn \(2 = {5^{{{\log }_3}x}}\) . Mệnh đề nào sau đây đúng?
\(2 = {5^{{{\log }_3}x}} \Leftrightarrow {\log _5}2 = {\log _3}x \Leftrightarrow \dfrac{{{{\log }_5}x}}{{{{\log }_5}3}} = {\log _5}2 \)
$\Leftrightarrow \dfrac{{{{\log }_5}x}}{{{{\log }_5}2}} = {\log _5}3 \Leftrightarrow {\log _5}3 = {\log _2}x \Leftrightarrow {\log _3}5 = {\log _x}2$
Suy ra $2 = {x^{{{\log }_3}5}}$
Biết phương trình \({9^x} - {2^{x + \frac{1}{2}}} = {2^{x + \frac{3}{2}}} - {3^{2x - 1}}\) có nghiệm là $a$. Tính giá trị của biểu thức \(P = a + \dfrac{1}{2}{\log _{\frac{9}{2}}}2\) .
Phương trình trên tương đương với
\({3^{2x - 2}} = {2^{x - \frac{3}{2}}} \) \(\Leftrightarrow {9^{x - 1}} = {2^{x - 1}}{.2^{\frac{{ - 1}}{2}}}\) \( \Leftrightarrow {(\dfrac{9}{2})^{x - 1}} = {2^{\frac{{ - 1}}{2}}} \)
$\Leftrightarrow x - 1 = {\log _{\frac{9}{2}}}{2^{\frac{{ - 1}}{2}}} $ $\Leftrightarrow x = 1 - \dfrac{1}{2}{\log _{\frac{9}{2}}}2$
Suy ra \(x + \dfrac{1}{2}{\log _{\frac{9}{2}}}2 = 1\)
Biết rằng phương trình ${2^{{x^2} - 1}} = {3^{x + 1}}$ có hai nghiệm là $a$ và $b$. Khi đó $a+ b + ab$ có giá trị bằng
Lấy $\ln $ hai vế ta được:
$\begin{array}{l}({x^2} - 1)\ln 2 = (x + 1)\ln 3 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\(x - 1)\ln 2 = \ln 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x - 1 = \dfrac{{\ln 3}}{{\ln 2}} = {\log _2}3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1 + {\log _2}3\end{array} \right.\end{array}$
Nếu $a = - 1;b = 1 + lo{g_2}3 \Rightarrow a + b + ab = \; - 1$.
Tìm các giá trị $m$ để phương trình \({2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3}}\) luôn thỏa, \(\forall x \in \mathbb{R}\).
\({2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3}}{\rm{ }} \Leftrightarrow {2^{x + 1}} = m{.2^{x + 1 + 1}} - {2^{x + 1 + 2}} \)
$\Leftrightarrow {2^{x + 1}} = m{.2.2^{x + 1}} - {2^2}{.2^{x + 1}} \Leftrightarrow {2^{x + 1}} = (2m - 4){2^{x + 1}}$
\( \Leftrightarrow 2m - 4 = 1 \Leftrightarrow m = \dfrac{5}{2}\)
Số nghiệm thực phân biệt của phương trình ${4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0$ là
$\begin{array}{l}{4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0 \Leftrightarrow {\left( {{2^{{x^2}}}} \right)^2} - {5.2^{{x^2}}} + 4 = 0 \Leftrightarrow \left( {{2^{{x^2}}} - 4} \right)\left( {{2^{{x^2}}} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{2^{{x^2}}} = 4\\{2^{{x^2}}} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = 2\\{x^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm \sqrt 2 \\x = 0\end{array} \right.\end{array}$
Trong các phương trình sau đây, phương trình nào có nghiệm?
Ý A: Điều kiện $x > 0$. Có ${x^{\frac{2}{3}}} + 5 > 0,\forall x > 0$ nên phương trình vô nghiệm
Ý B: Điều kiện $x > 4$. Có ${\left( {3x} \right)^{\frac{1}{3}}} + {\left( {x - 4} \right)^{\frac{2}{3}}} > 0,\forall x > 4$ nên phương trình vô nghiệm
Ý C: Điều kiện $x \ge 2$. Có $\sqrt {4x - 8} + 2 > 0,\forall x \ge 2$ nên phương trình vô nghiệm
Ý D: Điều kiện $x > 0$. Có $2{x^{\frac{1}{2}}} - 3 = 0 \Leftrightarrow {x^{\frac{1}{2}}} = \dfrac{3}{2} \Leftrightarrow x = {\log _{\frac{1}{2}}}\dfrac{3}{2}$ (thỏa mãn)
Cho $a$ là số thực dương, khác $1$ và thỏa mãn $\dfrac{1}{2}\left( {{a^\alpha } + {a^{ - \alpha }}} \right) = 1$ . Tìm $\alpha $
Áp dụng bất đẳng thức Cauchy ta có \({a^\alpha } + {a^{ - \alpha }}\; \geqslant 2\) .
Dấu "=" xảy ra khi \({a^\alpha } = {a^{ - \alpha }}\). Điều này dẫn đến \(\alpha = - \alpha \Rightarrow \alpha = 0\)
Cho \({4^x} + {4^{ - x}} = 7\). Khi đó biểu thức \(P = \dfrac{{5 - {2^x} - {2^{ - x}}}}{{8 + {{4.2}^x} + {{4.2}^{ - x}}}} = \dfrac{a}{b}\) với \(\dfrac{a}{b}\) tối giản và \(a,b \in \mathbb{Z}\). Tích \(a.b\) có giá trị bằng
\(\begin{array}{l}{4^x} + {4^{ - x}} = 7\\{4^x} + {4^{ - x}} + 2 = 9\\ \Leftrightarrow {\left( {{2^x}} \right)^2} + {\left( {{2^{ - x}}} \right)^2} + {2.2^x}{.2^{ - x}} = 9\\ \Leftrightarrow {\left( {{2^x} + {2^{ - x}}} \right)^2} = 9\\ \Leftrightarrow {2^x} + {2^{ - x}} = 3\end{array}\)
(do \({2^x} + {2^{ - x}} > 0\))
Vậy
\(\begin{array}{l}P = \dfrac{{5 - {2^x} - {2^{ - x}}}}{{8 + {{4.2}^x} + {{4.2}^{ - x}}}}\\\,\,\,\, = \dfrac{{5 - \left( {{2^x} + {2^{ - x}}} \right)}}{{8 + 4\left( {{2^x} + {2^{ - x}}} \right)}}\\\,\,\,\, = \dfrac{{5 - 3}}{{8 + 4.3}} = \dfrac{1}{{10}}\\ \Rightarrow a = 1,b = 10 \Rightarrow a.b = 1.10 = 10\end{array}\)
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để phương trình \({16^x} - {2.12^x} + \left( {m - 2} \right){.9^x} = 0\) có nghiệm dương?
Ta có \({16^x} - {2.12^x} + \left( {m - 2} \right){.9^x} = 0\)(1)
\( \Leftrightarrow {\left( {\frac{4}{3}} \right)^{2x}} - 2.{\left( {\frac{4}{3}} \right)^x} + m - 2 = 0\); chia cả hai vế cho \({9^x}\).
Đặt \({\left( {\frac{4}{3}} \right)^x} = t \Rightarrow x = {\log _{\frac{4}{3}}}t > 0 \Leftrightarrow t > 1\)
Khi đó ta có phương trình \({t^2} - 2t + m - 2 = 0\)(*)
Để phương trình (1) có nghiệm dương thì phương trình (*) có nghiệm lớn hơn 1.
(*) có nghiệm \( \Leftrightarrow \Delta ' = 1 - m + 2 \ge 0 \Leftrightarrow 3 - m \ge 0 \Leftrightarrow m \le 3\)
Với \(m \le 3\) thì \(\left( * \right)\) có nghiệm \({t_1} = 1 - \sqrt {3 - m} ,{t_2} = 1 + \sqrt {3 - m} \)
Để (*) có nghiệm lớn hơn 1 thì
\(1 + \sqrt {3 - m} > 1 \Leftrightarrow \sqrt {3 - m} > 0\) \( \Leftrightarrow 3 - m > 0 \Leftrightarrow m < 3\)
Mà \(m\) nguyên dương nên \(m \in \left\{ {1;2} \right\}\).
Vậy có 2 giá trị của \(m\) thỏa mãn.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
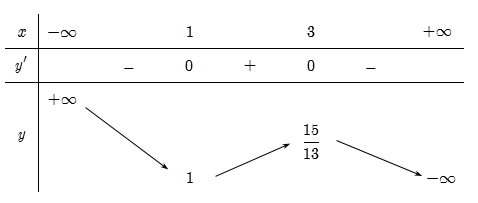
Biết $f\left( 0 \right) = \dfrac{7}{6}$, giá trị lớn nhất của \(m\) để phương trình \({e^{2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2}}} = m\) có nghiệm trên đoạn \(\left[ {0;\,2} \right]\) là
Ta có: \({e^{2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2}}} = m \Leftrightarrow 2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2} = \ln m\)
Xét \(g\left( x \right) = 2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2}\) có:
\(g'\left( x \right) = 6{f^2}\left( x \right)f'\left( x \right) - 13f\left( x \right)f'\left( x \right) + 7f'\left( x \right) = f'\left( x \right)\left[ {6{f^2}\left( x \right) - 13f\left( x \right) + 7} \right]\)
Suy ra \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\6{f^2}\left( x \right) - 13f\left( x \right) + 7 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\f\left( x \right) = 1\\f\left( x \right) = \dfrac{7}{6}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1;x = 3\\x = 1,x = {x_1} > 3\\x = {x_2} < 1\end{array} \right.\)
Xét \(g\left( x \right)\) trên đoạn \(\left[ {0;2} \right]\).
+ Trong khoảng \(\left( {0;1} \right)\) thì \(f'\left( x \right) < 0,f\left( x \right) > 1,f\left( x \right) < f(0)=\dfrac{7}{6}\) nên \(f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \dfrac{7}{6}} \right) > 0\) hay \(g'\left( x \right) > 0\).
+ Trong khoảng \(\left( {1;2} \right)\) thì \(f'\left( x \right) > 0,f\left( x \right) > 1,f\left( x \right) <\dfrac{15}{13}< \dfrac{7}{6}\) nên \(f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \dfrac{7}{6}} \right) < 0\) hay \(g'\left( x \right) < 0\).
Từ đó ta có bảng biến thiên của \(g\left( x \right)\) như sau:
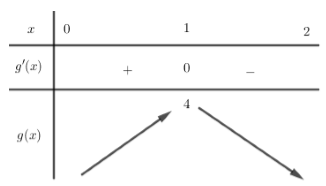
Từ bảng biến thiên ta thấy \(\mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right) = 4\).
Vậy yêu cầu bài toán thỏa nếu và chỉ nếu \(\ln m \le 4 \Leftrightarrow m \le {e^4}\) hay giá trị lớn nhất của \(m\) là \(m = {e^4}\).
Phương trình \({2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x\) có tổng các nghiệm gần nhất với số nào dưới đây:
\({2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x \Leftrightarrow {2^{23{x^3} + x}} + 23{x^3} + x = {2^{10{x^2}}} + 10{x^2}\)
Xét hàm số \(f(t) = {2^t} + t;f'(t) = {2^t}\ln 2 + 1 > 0,\forall t\)
\( \Rightarrow f(23{x^3} + x) = f(10{x^2}) \Leftrightarrow 23{x^3} + x = 10{x^2} \Leftrightarrow x(23{x^2} - 10x + 1) = 0\)
Theo vi-et cho phương trình bậc 3 ta có \({x_1} + {x_2} + {x_3} = - \dfrac{b}{a} = \dfrac{{10}}{{23}} \approx 0,45\)

